Рівняння плоскої хвилі

Рівняння хвилі — це формула, яка дає можливість знайти зміщення s від положення рівноваги частинки, координати якої х,у,z у момент часу t , тобто s (x, y, z, t).

Уявимо собі, що існує джерело у вигляді нескінченної площини, перпендикулярної до осі х і розміщеної на початку координат, тобто при x = 0. Кожна точка площини здійснює гармонічні коливання, рівняння яких: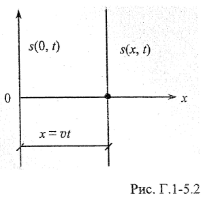

Очевидно, що хвильові поверхні теж будуть плоскі і тому хвиля буде одновимірною. Розглянемо коливання в точці, координата якої х. Частинка. яка міститься в цій точці, коливається з тією самою частотою, як і частинки біля джерела, і з амплітудою s₀ , але із запізненням.

Час τ, який потрібен хвилі, щоб дійти до цієї точки,

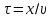
Тому рівняння коливань частинки буде таким:

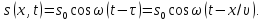
Ось так легко і просто ми отримали абсолютно правильне РІВНЯН­НЯ ПЛОСКОЇ ХВИЛІ. У цьому рівнянні: s — зміщення частинки з по­ложення рівноваги; 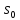— амплітуда коливань; х — координата; t — момент часу; 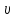— фазова швидкість.

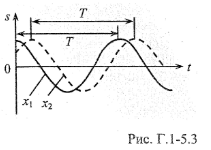
Врахувавши, що

,

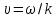запишемо рівняння плоскої хвилі в ін­шому, більш поширеному вигляді:

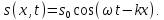
Якщо хвиля поширюється у від’ємному напрямі осі х, то потрібно змінити знак перед координатою х, тобто

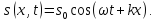
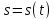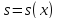У рівнянні хвилі дві змінні: х і s. Тому, коли з’являється необхідність графічно зобразити хвилю, будують залежність зміщення від часу при сталому x , або залежність зміщення від коор­динати при сталому часі (дивись рисунки).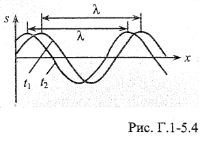

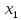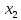У першому випадку ми дістанемо звичайний графік гар­монічних коливань для частинок із координатами і . Видно, що амп­літуди і періоди обох коливань однакові, а фази — різні.

У другому випадку ми отримаємо «миттєві знімки» біжучої хвилі для двох різних моментів часу 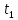і 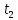На останньому графіку показано, що відстань між частинками, які здійснюють коливання в од­ній фазі (довжина хвилі), залишається сталою.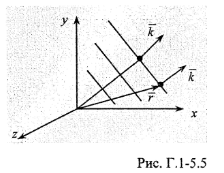

У загальному випадку плоска хвиля може поширюватись не вздовж осі х, а в довільному напрямі. Тоді 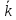буде вже вектором, а положення точки слід задавати, як звичайно, за допомогою радіуса-вектора 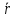. Рів­няння плоскої хвилі набере вигляду

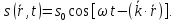
Можна розписати скалярний добуток хвильового вектора 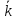на радіус-вектор :

,

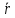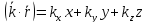і тоді рівняння набере вигляду

.

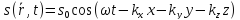Напрям поширення хвилі збігається з напрямом хвильового вектора, а він перпендикулярний до хвильової поверхні.

Рівняння сферичної хвилі

Сферична хвиля створюється точковим джерелом. Хвильові поверхні — це сфери. Хвильовий вектор у будь-якій точці перпендикулярний до хвильової поверхні, тобто збігається за напрямом з радіусом-вектором.

На відміну від плоскої хвилі амплітуда коливань частинок із мірою віддалення від джерела зменшується, тому через кожну наступну сферу протікає одна й та сама енергія, яка виділяється джерелом, але число час­тинок, які коливаються, зростає, як .

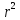Кожній частинці припадає менше енергії, і її амплітуда зменшується за законом 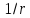. Рівняння сферичної хвилі:

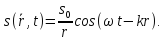
Зазначимо, що напрям фазової швидкості 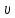збігається з напрямом хвильового вектора k і з напрямом радіуса-вектора .

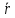Зауважимо також, що наведені рівняння плоскої та сферичної хвиль придатні як для поздовжніх, так і для поперечних хвиль.