1 курс / Л-3.2 (2) Додавання коливань

ДОДАВАННЯ КОЛИВАНЬ

1.Векторна форма зображення коливань

Використовується аналогія обертального і коливального руху. Вона полягає в тому, що рівняння руху для проекції обертового вектора збігається за формою з рівнянням гармонічних коливань.

Вектор R обертається зі сталою кутовою швидкістю (див. рисунок). За час t він повернеться на кут і проекція вектора на вісь x матиме вигляд:

Якщо в початковий момент часу вектор R перебував під кутом до вісі x, то

х = R cos().

Це рівняння повністю збігається за формою з рівнянням гармонічних коливань:

х = A cos().

Тобто:

Коливання можна уявити у вигляді обертового вектора, довжина якого R дорівнює амплітуді коливань А, кутова швидкість обертання - дорівнює циклічній частоті коливань , а початковий кут нахилу - початковій фазі коливань .

2. Комплексні числа та дії з ними. Показникова форма зображення коливань

Число виду

(1)

називається комплексним числом, записаним в алгебраїчній формі. Тут: - дійсна (real) частина, - уявна частина комплексного числа - уявна одиниця. Число з протилежною за знаком уявною частиною називається комплексно спряженим числом до комплексного числа z.

Як будь-якому дійсному числу на числовій осі відповідає точка, так комплексному числу Z відповідає точка на комплексній площині X0Y. Положення точки Z на площині можна задати полярними координатами ρ і φ. Зв’язок між полярними і декартовими координатами очевидний із рисунку

, (2)

. (3)

Підстановка (2) в (1) дає тригонометричну форму комплексного числа

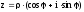. (4)

ρ – модуль комплексного числа, φ – його аргумент.

З математики відомі формули розкладання в степеневий ряд таких функцій (е = 2,718… – основа натурального логарифма):

, (5)

, (6)

, (7)

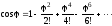. (8)

У формулі (6) згрупуємо члени у відповідності з формулами (7), (8)

.

Отже тригонометрична форма комплексного числа (4) може бути перетворена в показову форму

. (9)

Додавання і віднімання комплексних чисел зручно виконувати у алгебраїчній (1) чи в тригонометричній (4) формах шляхом зведення подібних членів. Але можна виконати ці операції і в показниковій формі, зображаючи кожне комплексне число як вектор (див. рисунок), довжина якого дорівнює модулю, а положення вектора задається аргументом φ, відрахованим від дійсної осі Х в позитивному напряму проти годинникової стрілки. При цьому використовуються правила додавання і віднімання векторів, наприклад, правило паралелограма.

Множення, ділення, піднесення до степеня зручніше виконувати з показниковою формою комплексних чисел, наприклад,

, , .

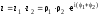Таким чином, за теоремою Ейлера для комплексних чисел:

де е - основа натурального логарифма, .

Тоді можна ввести поняття: КОМПЛЕКСНЕ ЗМІЩЕННЯ :

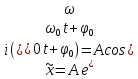) + iAsin().

Фізичне значення має тільки реальна частина комплексного зміщення, тобто істинне зміщення

х = Re () =).

Показникова форма використовується при розрахунках кіл змінного струму. Спочатку всі обчислення ведуться в комплексній формі, а потім відокремлюється дійсна частина.

3. Додавання двох коливань однокової частоти

Одне й те саме тіло може одночасно брати участь у кількох рухах. Наприклад, людина, яка їде в поїзді, здійснює коливання на м'якій лаві, а весь вагон здійснює коливання на власних ресорах. Кожне коливання здійснюється незалежно від інших. Коли кажуть про додавання коливань, то розуміють під цим відшукання результуючого рівняння руху, або рівняння траєкторії.

Розглянемо спочатку додавання двох коливань однокової частоти.

Вихідні рівняння коливань:

x₁ = A₁ cos(),

x₂ = A₂ cos().

Циклічна частота обох коливань однакова, а амплітуди і початкові фази різні. Для того щоб знайти рівняння руху результуючого коливання, зручно скористатися векторною діаграмою (див.рисунок). Уявимо обидва коливання у вигляді обертових з кутовою швидкістю векторів довжиною А₁ і А₂. Один відносно одного вектори нерухомі. Неважко зрозуміти, що різниця фаз коливань у будь-який момент часу буде сталою і дорівнюватиме різниці їхніх початкових фаз:

Коливання, різниця фаз яких залишається сталою з плином часу, називаються КОГЕРЕНТНИМИ КОЛИВАННЯМИ.

Як видно з векторної діаграми, вектор А, що дорівнює геометричній сумі векторів А₁ і А₂, подає результуюче коливання, рівняння якого легко записати:

x = A cos().

Частота результуючого коливання, очевидно, дорівнює частоті вихідних коливань, бо вектор А обертається з тією самою кутовою швидкістю. Амплітуду результуючого коливання дістанемо з теореми косинусів:

Проаналізуємо цей вираз. Якщо різниця фаз вихідних коливань дорівнює нулю, то амплітуда результуючого коливання дорівнює сумі амплітуд:

Якщо коливання здійснюються в протифазі, тобто ( то сумарна амплітуда дорівнює різниці цих амплітуд:

.

Якщо при цьому амплітуди вихідних коливань однакові, то сумарна амплітуда дорівнюватиме нулю, тобто коливання повністю загасять одне одного.

Початкову фазу результуючого коливання також легко обчислити (див. рисунок):

.

4. Додавання двох коливань із близькими частотами

Рівняння вихідних коливань:

Амплітуди обох коливань однакові, початкові фази однакові, а частоти відрізняються на . Причому .

Складемо вихідні рівняння, скориставшись тригонометричними співвідношеннями для суми косинусів двох кутів:

У першому члені ми знехтували величиною порівнянно з . Співмножник змінюється з часом набагато повільніше, ніж , тому здобуте рівняння можна розглядати як рівняння гармонічного коливання частоти 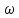, амплітуда якого сама змінюється за гармонічним законом.

Це добре унаочнює рисунок де зображено графік залежності зміщення від часу.

Такі коливання називаються БИТТЯМ. Амплітуда биття

.

Максимальне значення амплітуди биття дорівнює подвоєній амплітуді вихідних коливань . Частота зміни амплітуди биття дорівнює .

Биття - це окремий випадок так званої АМПЛІТУДНОЇ МОДУЛЯЦІЇ. Коливання називають амплітудно - модульованими, якщо амплітуда коливань не є сталою, а сама залежить від часу згідно з довільним законом. Рівняння амплітудно - модульованих коливань можна записати так:

Якщо амплітуда змінюється за періодичним законом, то частота зміни амплітуди називається ЧАСТОТОЮ МОДУЛЯЦІЇ (), а частота самих модульованих коливань - НЕСУЧОЮ ЧАСТОТОЮ ().

5. Додавання взаємно перпендикулярних коливань

Нехай матеріальна точка одночасно бере участь у двох коливаннях однакової частоти, які відбуваються вздовж осей x i y. Рівняння вихідних коливань:

,

Амплітуди коливань різні; - різниця фаз коливань 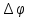визначається різницею початкових фаз. Рівняння руху обох коливань задані і завдання полягає лише в тому, щоб знайти рівняння траєкторії. Для цього потрібно просто вилучити час із рівнянь руху.

Виконавши це, дістанемо:

.

Як відомо, це рівняння еліпса, півосі якого не збігаються з напрямом осей координат. При зміні початкових амплітуд і різниці фаз можливі окремі випадки.

1. Різниця фаз дорівнює нулю: . Рівняння траєкторії набирає вигляду:

.

Траєкторія - відрізок прямої лінії, що проходить через початок координат (див. рис.). Вона нахилена до осі х під кутом тангенс якого дорівнює відношенню амплітуд: .

2. Різниця фаз Рівняння траєкторії набирає вигляду:

Це рівняння еліпса, зведене до координатних осей. Довжина півосей еліпса дорівнює амплітудам вихідних коливань (див. рис. ). Випадки відрізняються напрямом руху матеріальної точки по колу. У першому випадку рух відбувається за годинниковою стрілкою, у другому - проти.

При додаванні коливань, частоти яких різні, траєкторія в загальному випадку не буде сталою. Сталими траєкторії виходять тоді, коли частоти вихідних коливань кратні:

Такі сталі траєкторії називають ФІГУРАМИ ЛІСАЖУ.

На рисунку внизу наведено фігури Лісажу для відношення частот 2/1, 3/2 і 4/3. При цьому різниця фаз .