Добавил:

anna4514793 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Гомельский государственный университет им. Франциска Скорины

Предмет:

Математика

Файл:

топология / Топология 6. Связность. Компактность..doc

Скачиваний:

Добавлен:

24.10.2019

Размер:

1.23 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Контрольные задания

1.1 а) Показать, что если и - связные подмножества пространства и , то - связно.

б) Являются ли множества связными в естественной топологии, топологиях Зарисского, Зоргенфрея, дискретной, антидискретной и топологии стрелки,

1.2 а) Показать, что компонента пространства замкнута в .

1.3 а) Показать, что любые две компоненты пространства или совпадают, или не пересекаются.

1.4 а) Показать, что множество всех компонент пространства его покрывают.

1.5 а) Доказать, что отрезок связен.

1.6 а) Показать, что множества и в естественной топологии на не гомеоморфны.

1.7 а) Показать, что множества и в естественной топологии на не гомеоморфны.

1.8 а) Показать, что множества и в естественной топологии на не гомеоморфны.

1.9 а) Доказать, что множество является вполне несвязным в естественной топологии на .

1.10 а) Доказать, что множество является вполне несвязным в топологии Зоргенфрея на .

1.11 а) Доказать, что множество является вполне несвязным в естественной топологии на .

1.12 а) Доказать, что множество является вполне несвязным в топологии Зоргенфрея на .

1.13 а) Доказать, что пространство линейно связно.

1.14 а) Доказать, что если - собственное непустое подмножество связного топологического пространства, то .

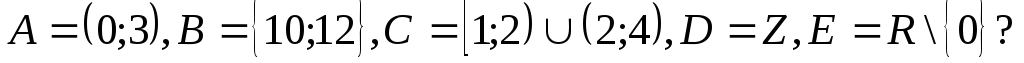
1.15 а) Пусть - связное множество пространства . Доказать связность .

1.16 а) Показать, что если и - связные подмножества пространства и, то - связно.

1.17 а) Показать, что пространство с антидискретной топологией связно.

1.18 а) Показать, что пространство с дискретной топологией связно тогда и только тогда, когда оно содержит не более одной точки.

1.19 а) Доказать, что топологическое пространство несвязно тогда и только тогда, когда существует такое непрерывное отображение , что .

1.20 а) Построить на числовой прямой два связных множества, таких, что их объединение было несвязным.

1.21 а) Построить на числовой прямой два связных множества, таких, что их пересечение было несвязным.

1.22 а) Показать, что открытый шар пространства - связное множество.

1.23 а) Пусть - последовательность связных множеств топологического пространства, для которых . Показать, что - связное множество.

1.24 а) Показать, что подмножество множества рациональных чисел в естественной топологии связно тогда и только тогда, когда оно одноточечно.

1.25 а) Показать, что две компоненты связности либо не пересекаются, либо совпадают.

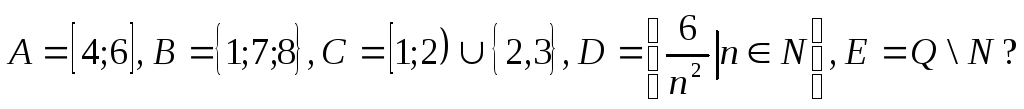
1.26 а) Показать, что пространство связно тогда и только тогда, когда любая пара его точек лежит в некотором связном подмножестве.

1.27 а) Показать, что компоненты связности замкнуты.

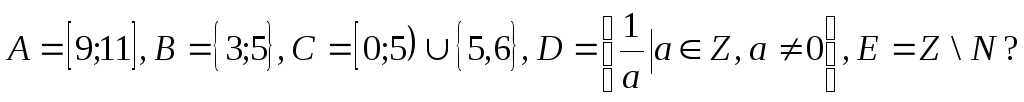
1.28 а) Доказать, что непрерывный образ линейно связного пространства линейно связен.

1.29 а) Показать, что интервал - линейно связен.

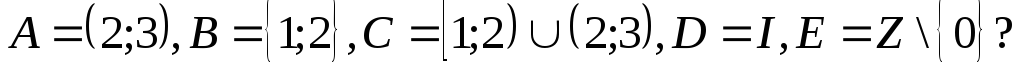
1.30 а) Показать, что выпуклое подмножество евклидова пространства является линейно связным.

2.1 а) Доказать, что компактное подмножество метрического пространства ограничено.

б) Являются ли множества из задания 1.б) компактными в естественной топологии, топологиях Зарисского, Зоргенфрея, дискретной, антидискретной и топологии стрелки.

2.2 а) Доказать, что замкнутое подмножество компактного пространства компактно.

а) Доказать, что компактное подмножество метрического пространства ограничено.

а) Доказать, что компактное хаусдорфово пространство регулярно.

2.5 а) Показать, что метрическое пространство является компактным тогда и только тогда, когда из всякой последовательности его точек можно выделить сходящуюся подпоследовательность.

2.6 а) Показать, что замкнутое подпространство компактного пространства компактно.

2.7 а) Показать, что метрическое пространство является компактным тогда и только тогда, когда всякая его убывающая последовательность непустых замкнутых множеств имеет непустое пересечение.

2.8 а) Показать, что любое компактное хаусдорфово пространство нормально.

2.9 а) Пусть ( с индуцированной из топологией) и . Показать, что не компактно.

2.10 а) Показать, что любое метризуемое компактное пространство сепарабельно.

б) Доказать, что множество всех неподвижных точек непрерывного отображения Хаусдорфова пространства в себя является замкнутым.

2.11 а) Пусть множества и компактны. Показать, что компактно и множество .

2.12 а) Доказать, что прямая не компактна.

2.13 а) Показать, что непрерывный образ компактного пространства компактен.

2.14 а) Сохраняется ли при непрерывном отображении нормальность топологических пространств.

2.15 а) Сохраняется ли при непрерывном отображении нормальность, если - непрерывное сюръективное отображение, переводящее каждое замкну-тое множество в замкнутое.

2.16 а) Доказать, что дискретная топология компактна на множестве тогда и только тогда, когда конечно.

2.17 а) Доказать, что бесконечное множество с дискретной топологией некомпактно.

а) Доказать, что бесконечное множество с дискретной топологией локально компактно.

2.19 а) Пусть - компактное топологическое пространство, и - непересекающиеся замкнутые множества в .Доказать, что существуют такие открытые множества в , содержащие и , которые не пересекаются.

2.20 а) Пусть - компактное пространство и - непрерывное отображение. Показать, что отображение ограничено и достигает на своего наибольшего и наименьшего значений.

2.21 а) Показать, что если подмножество компактно, а хаусдорфово, то - замкнуто.

2.22 а) Показать, что компактное хаусдорфово пространство нормально.

2.23 а) Привести пример компактного множества, замыкание которого некомпактно.

2.24 а) Показать, что компактное множество всегда замкнуто.

2.25 а) Показать, что компактное множество всегда ограничено.

2.26 а) Показать, что множество в естественной топологии на является компактным.

2.27 а) Доказать, что всякое замкнутое подмножество компактного множества является компактным.

2.28 а) Пусть множества и метрического пространства компактны. Доказать, что тогда из того, что следует .

2.29 а) Доказать, что любое непрывное взаимнооднозначное отображение, определенное на компактном множестве является гомеоморфизмом.

2.30 а) Показать, что прообраз компактного множества при непрерывном отображении может не быть компактным.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в папке топология

#
24.10.20191.48 Mб34Топология 1.Множества..doc
#
24.10.20192.1 Mб62Топология 2. Структура.doc
#
24.10.20191.5 Mб39Топология 3. Метр. простр..doc
#
24.10.20191.9 Mб50Топология 4. Непр. отобр..doc
#
24.10.2019920.06 Кб37Топология 5. Счетность. Отделимость..doc
#
24.10.20191.23 Mб57Топология 6. Связность. Компактность..doc
#
24.10.2019281.14 Кб29Топология 7.doc