
ЗАДАНИЕ 2.
ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА.
Основные понятия и определения.
-
Топологическая структура (топология).
Топологической
структурой (или топологией) в множестве
![]() называется
такая совокупность
его подмножеств, что:
называется
такая совокупность
его подмножеств, что:
-
объединение любого семейства множеств, принадлежащих , также принадлежит ;
-
пересечение любого конечного семейства множеств, принадлежащих , также принадлежит ;
-
и
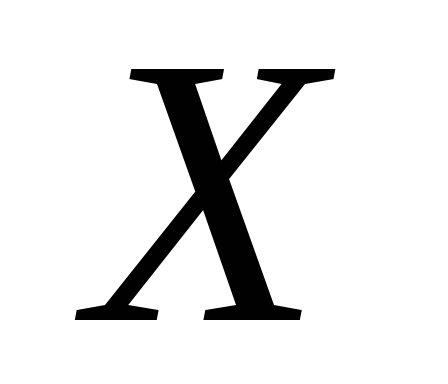 принадлежат .
принадлежат .
Множество
![]() с выделенной топологической структурой
(т.е. пара
с выделенной топологической структурой
(т.е. пара
![]() )
называется топологическим пространством.
Условия 1) - 3) называются аксиомами
топологической структуры.
)
называется топологическим пространством.
Условия 1) - 3) называются аксиомами
топологической структуры.
Если
![]() - топологическое пространство, то
элементы множества
- топологическое пространство, то
элементы множества
![]() называются точками, а элементы
множества -
открытыми множествами.
называются точками, а элементы
множества -
открытыми множествами.
Говорят,
что множество
![]() замкнуто в пространстве
замкнуто в пространстве
![]() ,
если его дополнение в
,
если его дополнение в
![]() открыто (т.е. если
открыто (т.е. если
![]() ).
).
Окрестностью точки топологического пространства называют любое открытое множество, содержащее эту точку.
Если 1
и 2
-топологические структуры в множестве
![]() и 1
2
, то говорят, что структура 2
тоньше, чем 1,
а 1
– грубее, чем 2.
При этом записывают 1
2.
и 1
2
, то говорят, что структура 2
тоньше, чем 1,
а 1
– грубее, чем 2.
При этом записывают 1
2.
Пусть
![]() - топологическое пространство,
- топологическое пространство,
![]() .
Обозначим через
.
Обозначим через
![]() совокупность множеств вида
совокупность множеств вида
![]() ,
где
,
где
![]() .
Совокупность
.
Совокупность
![]() называется относительной топологией
или топологией, индуцированной в
называется относительной топологией
или топологией, индуцированной в
![]() топологией
топологией
![]() ,
а её элементы - множествами, открытыми
в
,
а её элементы - множествами, открытыми
в
![]() .
.
Пусть
![]() - топологическое пространство,
- топологическое пространство,
![]() .
Обозначим через
.
Обозначим через
![]() совокупность множеств вида
совокупность множеств вида
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() есть топологическая структура в
есть топологическая структура в
![]() .
.
Пара
![]() называется подпространством
пространства
называется подпространством
пространства
![]() ,
совокупность
,
совокупность
![]() называется относительной топологией
или топологией, индуцированной в
называется относительной топологией
или топологией, индуцированной в
![]() топологией
топологией
![]() ,
а ее элементы называются множествами,
открытыми в
,
а ее элементы называются множествами,
открытыми в
![]() .
.
Примеры:
1.1 Дискретное
пространство - множество, в котором
топологией является множество всех его
подмножеств
![]() .
.
1.2 Aнтидискретное
пространство - противоположный пример,
в котором топологическая структура
состоит из
![]() и .
и .
1.3 Пусть
![]() есть луч [0; +), а
состоит из ,
есть луч [0; +), а
состоит из ,
![]() и всевозможных лучей
и всевозможных лучей
![]() ,
где
,
где
![]() .
Такое топологическое пространство
называется стрелкой.
.
Такое топологическое пространство
называется стрелкой.
1.4 Пусть
![]() - множество всех вещественных чисел,
- совокупность объединений всевозможных
семейств интервалов (интервалом
назовем множество вида
- множество всех вещественных чисел,
- совокупность объединений всевозможных
семейств интервалов (интервалом
назовем множество вида
![]() ,
где
,
где![]() ).
Такая совокупность является топологической
структурой. Она порождает естественную
топологию на
).
Такая совокупность является топологической
структурой. Она порождает естественную
топологию на
![]() .
Эту топологическую структуру имеют в
виду всегда, когда о множестве
.
Эту топологическую структуру имеют в
виду всегда, когда о множестве
![]() говорят как о топологическом пространстве,
не описывая явно топологию. Это
пространство называется обычно
вещественной прямой.
говорят как о топологическом пространстве,
не описывая явно топологию. Это
пространство называется обычно
вещественной прямой.
-
Рассмотрим множество, состоящее из двух различных точек:
 .
На нем можно задать четыре топологии:
.
На нем можно задать четыре топологии:
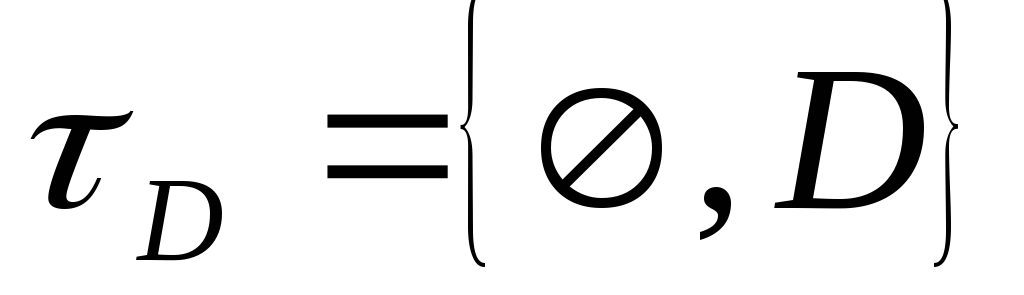 ,
,
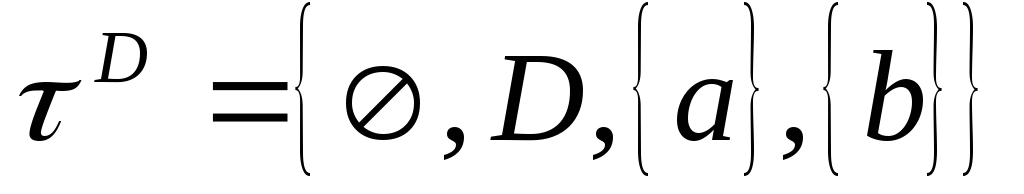 ,
,
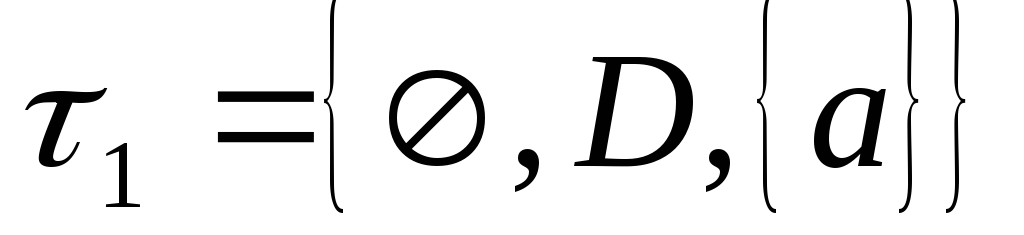 ,
и
,
и
 .
.
1.6 Рассмотрим
топологию
![]() .
Такая топология называется топологией
Зарисского.
.
Такая топология называется топологией
Зарисского.
-
Пусть
 - множество всех действительных чисел.
Рассмотрим совокупность
- множество всех действительных чисел.
Рассмотрим совокупность
 ,
состоящую из ,
,
состоящую из ,
 ,
полуинтервалов вида
,
полуинтервалов вида
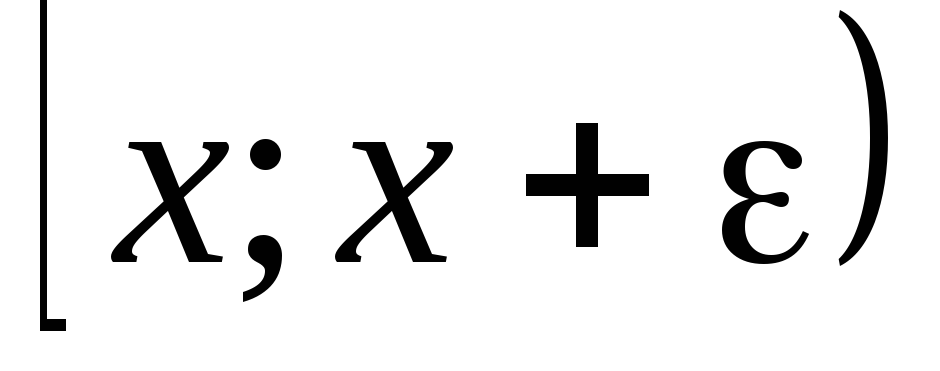 (
(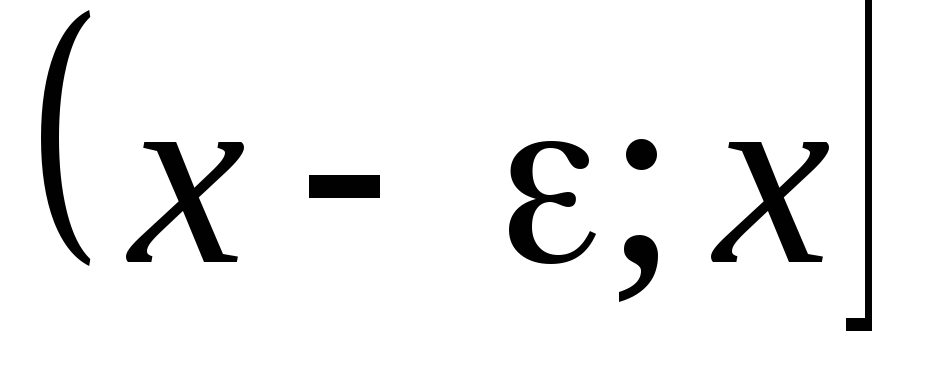 ),
где
),
где
 и их всевозможных объединений. Множество
и их всевозможных объединений. Множество
 образует топологию, которую называют
правой (левой) топологией Зоргенфрея.
образует топологию, которую называют
правой (левой) топологией Зоргенфрея. -
Открытые (замкнутые) множества открытого (замкнутого) подпространства открыты (замкнуты) во всем пространстве.
1.9 Стандартная топология с
![]() (топология,
индуцированная в
(топология,
индуцированная в
![]() )
как в подмножестве
)
как в подмножестве
плоскости, совпадают.
2.0 Единственным открытым множеством
прямой
![]() ,
(открытым и в
,
(открытым и в
![]() )
является .
)
является .
ОСНОВНЫЕ ТЕОРЕМЫ.
Теорема 10. ( Свойства замкнутых множеств):
1) пересечение любого набора замкнутых множеств замкнуто,
2) объединение любого конечного набора замкнутых множеств замкнуто,
-
пустое множество и все пространство (т.е. все множество – носитель топологической структуры) замкнуты.
Теорема 11. Множество замкнуто в подпространстве тогда и только тогда, когда оно индуцируется в нём множеством, замкнутым во всём пространстве.
Следствие 1. Пусть
![]() .
Тогда:
.
Тогда:
-
если
 открыто в
открыто в
 ,
то
,
то
 открыто и в
открыто и в
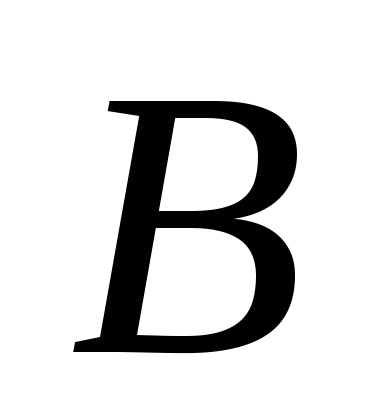 ;
; -
если
 замкнуто в
замкнуто в
 ,
то
,
то
 замкнуто и в
замкнуто и в
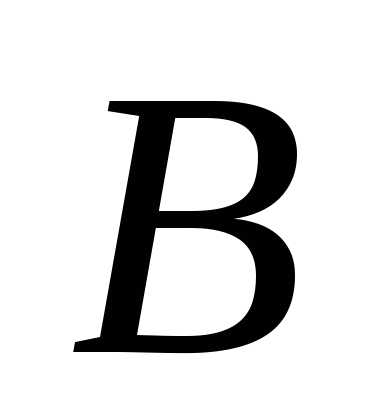 ;
; -
если
 открыто в
открыто в
 ,
а
,
а
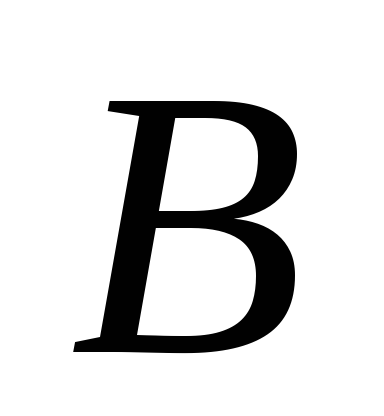 открыто в
открыто в
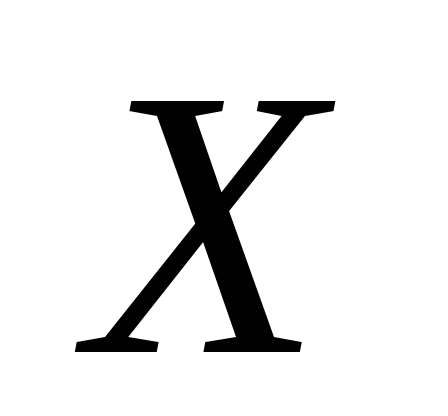 ,
то
,
то
 открыто и в
открыто и в
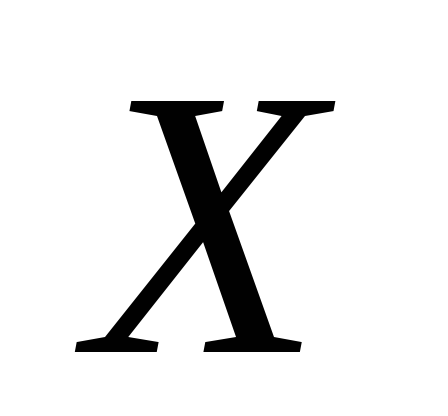 ;
; -
Если
 замкнуто в
замкнуто в
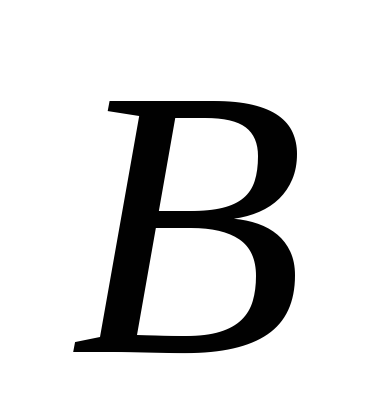 ,
а
,
а
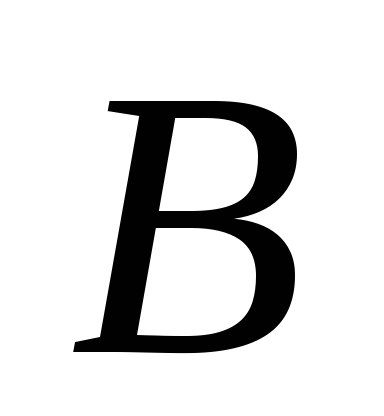 замкнуто в
замкнуто в
 ,
то
,
то
 замкнуто в
замкнуто в
 .
.
Лемма 1.
Бинарное отношение
на множестве всех топологий пространства
![]() есть
отношение частичного порядка.
есть
отношение частичного порядка.
Теорема
12. Пусть
![]() - некоторое семейство топологий множества
- некоторое семейство топологий множества
![]() .
Тогда
.
Тогда
![]() является топологией множества
является топологией множества
![]() и
и
![]() для любой топологии
для любой топологии
![]() множества
множества
![]() .
.
Следствие.
Пусть
![]() -
система подмножеств множества
-
система подмножеств множества
![]() .
Тогда существует наименьшая топология
в
.
Тогда существует наименьшая топология
в
![]() содержащая систему
содержащая систему
![]() .
.
-
База топологии.
Базой топологии называется такая совокупность открытых множеств, что всякое непустое открытое множество представимо в виде объединения множеств этой совокупности. Элементы базы называют элементарными открытыми множествами.
Топология может иметь несколько или даже бесконечное число баз.
Наименьшая
из мощностей всех возможных баз топологии
на
![]() называется весом пространства
называется весом пространства
![]() .
.
Базы, задающие одну и ту же топологическую структуру, называются эквивалентными.
Произвольное
семейство
![]() некоторых окрестностей точки
некоторых окрестностей точки
![]() называется локальной базой в точке
называется локальной базой в точке
![]() ,
если для любой окрестности
,
если для любой окрестности
![]() этой точки найдётся окрестность
этой точки найдётся окрестность
![]() ,
что
,
что
![]() .
.
Объединение некоторых
локальных баз всех точек пространства
![]() называется базой окрестностей или
фундаментальной системой окрестностей
(ФСО) топологии
называется базой окрестностей или
фундаментальной системой окрестностей
(ФСО) топологии
![]() .
.
Для задания топологии
достаточно указать некоторую ФСО
![]() .
В этом случае о топологии
.
В этом случае о топологии
![]() говорят, что она порождена ФСО
говорят, что она порождена ФСО
![]() .
.
ОСНОВНЫЕ ТЕОРЕМЫ.
Теорема
13. Совокупность
![]() открытых множеств является базой
топологии тогда и только тогда,
если для всякого открытого множества
X и всякой точки
открытых множеств является базой
топологии тогда и только тогда,
если для всякого открытого множества
X и всякой точки
![]() существует такое множество
существует такое множество
![]() ,
что
,
что
![]() .
.
Теорема
14. Совокупность
![]() подмножеств множества
подмножеств множества
![]() является базой некоторой топологии в
является базой некоторой топологии в
![]() тогда и только тогда, когда
тогда и только тогда, когда
![]() есть
есть
объединение
множеств из
![]() и пересечение любых двух множеств из
и пересечение любых двух множеств из
![]() ,
,
представляется
в виде объединения множеств из
![]() .
.
Теорема
15. Пусть
![]() -
произвольное множество. Каждой точке
-
произвольное множество. Каждой точке
![]() поставим в соответствие некоторое
семейство
поставим в соответствие некоторое
семейство
![]() подмножеств множества
подмножеств множества
![]() .
Семейство
.
Семейство![]() является ФСО для некоторой топологии
является ФСО для некоторой топологии
![]() тогда и только тогда, когда выполняются
следующие условия (аксиомы ФСО):
тогда и только тогда, когда выполняются
следующие условия (аксиомы ФСО):
1) для любой
точки
![]() существует такое непустое подсемейство
существует такое непустое подсемейство
![]() ,
что для любого
,
что для любого
![]() справедливо
справедливо
![]() ;
;
2) для любых
![]() и
и
![]() найдётся
найдётся
![]() такое, что
такое, что
![]() ;
;
-
для любых
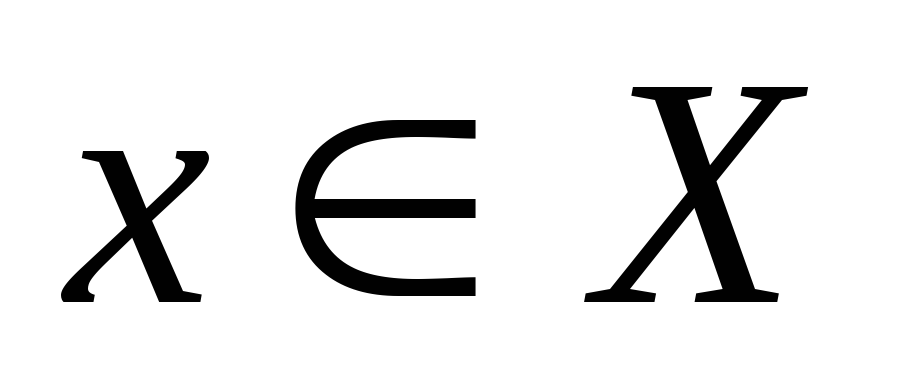 ,
,
 и
и
 найдётся
найдётся
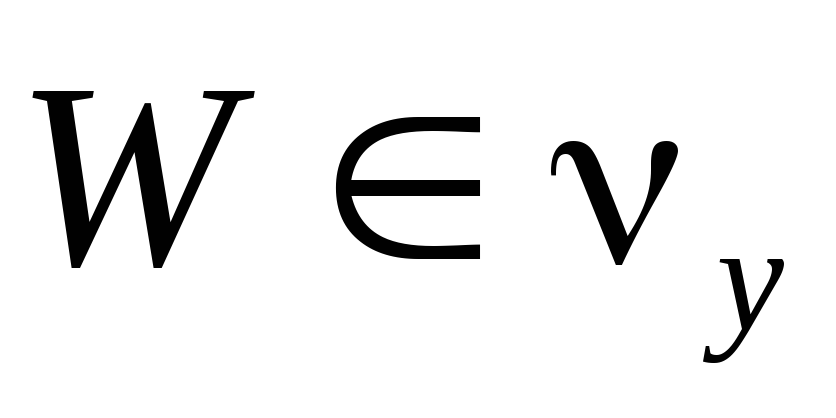 такое, что
такое, что
 .
.
Теорема 16. Пусть
![]() и
и
![]() на множестве
на множестве
![]() порождены некоторыми ФСО
порождены некоторыми ФСО
![]() и
и
![]()
соответственно.
Соотношение 1
2
имеет место тогда и только тогда,
когда для любых
![]() и
и
![]() найдётся окрестность
найдётся окрестность
![]() такая, что
такая, что
![]() .
.
Следствие.
Две ФСО
![]() и
и
![]() на множестве
на множестве
![]() порождают одну и ту же топологию
порождают одну и ту же топологию
![]() ,
когда для любой точки
,
когда для любой точки
![]() и её окрестностей
и её окрестностей
![]() и
и
![]() найдутся
найдутся
![]() и
и
![]() ,
такие, что
,
такие, что
![]() ,
,
![]()
Теорема
17. Любая ФСО
![]() в пространстве
в пространстве
![]() является базой некоторой топологии
является базой некоторой топологии
![]() .
Обратно, любая база топологии
.
Обратно, любая база топологии
![]() является ФСО в пространстве
является ФСО в пространстве
![]() .
.
Теорема
18. Пусть
![]() - топологическое пространство,
- некоторая топология в
- топологическое пространство,
- некоторая топология в
![]() ,
,
![]() - база топологии
- база топологии
![]() ,
,
![]() .
Тогда
.
Тогда
![]() - база, индуцированная топологией
- база, индуцированная топологией
![]() .
.
