-
Геометрия топологического пространства.
Пусть
- топологическое пространство,
.
Окрестностью точки
называется любое открытое множество
,
содержащее точку
.
Пусть подмножество
.
Точка
называется:
-
внутренней точкой множества
,
если она обладает окрестностью,
содержащейся в
; -
внешней точкой множества
,
если она обладает окрестностью, не
пересекающейся с
; -
граничной точкой множества
,
если всякая её окрестность имеет
непустое пересечение как с множеством
так и с его дополнением в
; -
точкой прикосновения множества
,
если всякая её окрестность имеет
непустое пересечение с
.
-
предельной точкой множества
,
если всякая ее окрестность пересекается
с А\{х}. -
изолированной точкой множества
,
если
и существует окрестность точки
,
не пересекающаяся с
. -
предельной точкой множества
,
если любая её окрестность содержит
бесконечно много точек из
.
- множество всех внутренних точек
(наибольшее по включению открытое
множество, содержащееся в
).
- замыкание множества
в топологическом пространстве
или множество всех точек прикосновения
множества
( наименьшее замкнутое множество в
,
содержащее
).
- множество всех граничных точек множества
(граница
)
в топологическом пространстве
(
,
).
Внешностью
множества
(
)
называется наибольшее не пересекающееся
с ним открытое множество. Ясно, что
внешность совпадает с
.
Подмножество
топологического пространства
называется канонически открытым,
если
.
Подмножество
топологического пространства
называется канонически замкнутым,
если
.
ОСНОВНЫЕ ТЕОРЕМЫ.
Теорема 19.
Множество
замкнуто тогда и только тогда, когда
,
т. е. когда
содержит все свои точки прикосновения.
Теорема 20. Для
любого множества
справедливо равенство
Теорема 21.
Множество
открыто тогда и только тогда, когда
Теорема 22. (О свойствах внутренности множества):
-
; -
если
,
то
; -
; -
; -
; -
.
Теорема 23. (О свойствах замыкания):
1)
;
2) если
,
то
;
-
; -
; -
.
Теорема 24. (О свойствах границы):
-
; -
; -
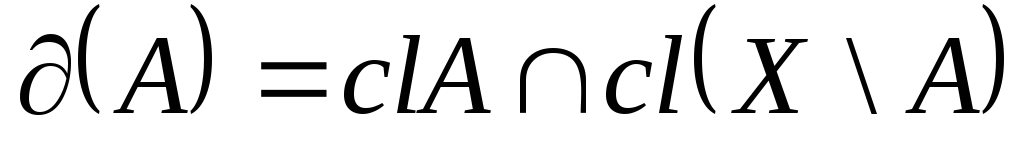Следствие 1.
Для любого
граница
есть замкнутое множество.
Следствие 2.
Для любого
замыкание
,
причём
.
Примеры:
3.1 В
с естественной топологией
,
.
3.2 Граница
множества
всегда совпадает с множеством всех
своих граничных точек.
3.3 Рассмотрим
множества
и
на вещественной прямой
с естественной топологией. Имеем
.
3.4 Для множеств
рациональных чисел и
иррациональных чисел на вещественной
прямой
имеем
.
3.5 В
:
,
.
3.6 Граница
множества
совпадает с множеством граничных точек
множества
.
3.7 Рассмотрим
множества
и
на вещественной прямой
с естественной топологией. Имеем
.
3.8 Для множеств
рациональных чисел и
иррациональных чисел на вещественной
прямой
имеем
.
Контрольные задания
-
а) Пусть
состоит из четырёх элементов
.
Проверить, является ли совокупность
топологией на
,
и, в случае отрицательного ответа,
дополнить её до топологии.
б) Пусть
- некоторое семейство подмножеств в
и
- подмножество в
.
Пусть
.
Показать, что:
= топология; построить две различные
базы
;
построить примеры топологий сильнее и
слабее
.
1.1 а)
.
б)
.
-
а)
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
1.5 а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
1.12 а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
1.16 а)
.
б)
.
-
а)
.
б)
.
-
а)
.
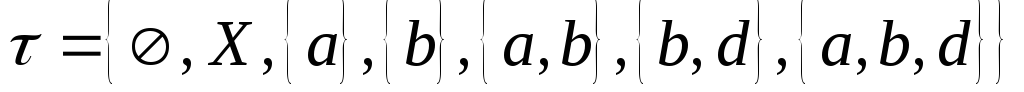б)
.
-
а)
.
б)
.
1.20 а)
.
б)
.
1.21 а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
-
а)
.
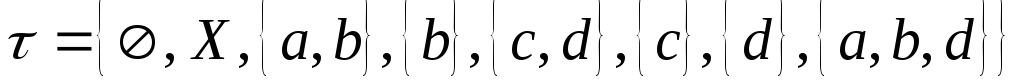б)
.
-
а)
.
б)
.
-
а)
.
б)
.
1.27 а)
.
б)
.
1.28 а)
.
б)
.
-
а)
.
б)
.
-
а)
.
б)
.
2.1 а) Пусть
- топологическое пространство и
-
его некоторое подмножество. Положим
.
Показать, что
- топология на
.
б) Построить ФСО
естественной топологии на
.
-
а) Показать, что объединение двух топологий на
может не быть топологией.
б) Построить ФСО
топологии Зарисского на
.
-
а) Показать, что пересечение двух топологий на
является топологией на
.
б) Построить все
топологии, которые можно задать на
множестве
,
состоящем из четырёх элементов. Найти
их ФСО.
2.4 а) Показать, что всевозможные бесконечные арифметические прогрессии, состоящие из натуральных чисел, образуют базу некоторой топологии в N.
б) Построить 2
примера множеств в естественной топологии
на
,
являющимися одновременно открытыми и
замкнутыми.
2.5 а) Описать топологии, которые индуцируются в множестве натуральных чисел N естественной топологией, топологией Зоргенфрея, топологией Зарисского.
б) Построить три
примера топологий на плоскости
.
Указать примеры ФСО для них.
2.6 а) Пусть
и
-
граница множества
.
Элементарной окрестностью точки
называется множество вида
,
где
,
а элементарной окрестностью точки
множество вида
,
где
.
Показать, что семейство
всех таких элементарных окрестностей
является фундаментальной системой
окрестностей ( Ф С О ) точки
.
б) Построить топологию
на множестве
,
аналогичную топологии Зарисского на
.
Дать геометрическую интерпретацию
открытым и замкнутым множествам
полученного топологического пространства.
2.7 а) Пусть
- естественная топология на
.
Построить два примера топологий на
,
слабее
.
б) Построить ФСО
топологии Зоргенфрея на
.
2.8 а) Пусть
.
Построить две различные топологии на
.
Указать примеры ФСО для них.
б)
Показать,
что множество
замкнуто тогда и только тогда, когда
.
2.9 а) Пусть
- естественная топология на
.
Построить два примера топологий на
,
сильнее
.
Указать ФСО для них.
б) Пусть
состоит из четырёх элементов
Построить на
три различные топологии.
2.10 а) Пусть
- луч, а
состоит из
и всевозможных лучей
,
где
.
Доказать, что
- топология на
.
Указать пример ФСО для неё.
б) Доказать, что
множество
открыто тогда и только тогда, когда оно
содержит некоторую окрестность каждой
своей точки.
2.11 а) Доказать, что
подмножество
топологического пространства замкнуто
тогда и только тогда, когда
.
б) Пусть множество
замкнуто, а множество
- открыто. Доказать, что
-замкнуто, а
- открыто.
2.12 а) Построить на
топологии, индуцированные естественной
топологией на прямой, топологией
Зарисского, топологией Зоргенфрея.
Привести примеры ФСО для них.
б) Доказать, что для любых двух непересекающихся открытых множеств замыкание одного множества не пересекается с другим множеством.
2.13 а) Построить ФСО
топологии на
,
индуцированной на нём естественной
топологией на
.
б) Показать, что объединение конечного числа замкнутых множеств является замкнутым множеством.
2.14 а) Построить ФСО
топологии на
,
индуцированной на нём естественной
топологией.
б) Показать, что
множество
замкнуто тогда и только тогда в
пространстве
,
когда
.
-
а) Описать топологию на множестве
,
индуцированной естественной топологией,
топологиями Зарисского, Зоргенфрея.
Указать примеры ФСО для них.
б) пусть множество
открыто и
.
Доказать, что
.
2.16 а) Пусть
- топологическое пространство.
Положим
.
Показать, что
- топология на
.
б) Построить ФСО
естественной топологии на
.
-
а) Проверить, будет ли топологией на
объединение
дискретной и естественной топологий.
б) Построить ФСО
топологии на
,
индуцированной топологией Зарисского.
-
а) Показать, что пересечение топологии Зарисского и Зоргенфрея на
является топологией на
.
б) Построить все
топологии, которые можно задать на
множестве
,
состоящем из трех элементов. Найти их
ФСО.
2.19 а) Построить топологию, базой которой является множество иррациональных чисел.
б) Построить 2
примера множеств в топологии стрелки
на
,
являющимися одновременно открытыми и
замкнутыми.
2.20 а) Описать топологии,
которые индуцируются в множестве
естественной топологией, топологией
Зоргенфрея, топологией Зарисского.
б) Построить три
примера топологий на пространстве
.
Указать примеры ФСО для них.
2.21 а) Пусть
и
-
граница множества
.
Элементарной окрестностью точки
называется множество вида
,
где
,
а элементарной окрестностью точки
множество вида
,
где
.
Показать, что семейство
всех таких элементарных окрестностей
является фундаментальной системой
окрестностей ( Ф С О ) точки
.
б) Построить топологию
на множестве
,
аналогичную топологии Зарисского на
.
Дать геометрическую интерпретацию
открытым и замкнутым множествам
полученного топологического пространства.
2.22 а) Пусть
- топология Зоргенфрея на
.
Построить два примера топологий на
,
слабее
.
б) Построить ФСО
дискретной топологии на
.
2.23 а) Пусть
.
Построить две различные топологии на
.
Указать примеры ФСО для них.
б)
Показать,
что множество
открыто если множество
пусто.
2.24 а) Пусть
- естественная топология на
.
Построить два примера топологий на
,
сильнее
.
Указать ФСО для них.
б) Пусть
состоит из пяти элементов
Построить на
три различные топологии.
2.25 а) Пусть
- луч, а
состоит из
и всевозможных лучей
,
где
.
Доказать, что
- топология на
.
Указать пример ФСО для неё.
б) Доказать, что
множество
открыто в
тогда
и только тогда, когда его дополнение в
содержит границу.
2.26 а) Доказать, что
подмножество
топологического пространства открыто
тогда и только тогда, когда
.
б) Пусть множество
открыто, а множество
- замкнуто. Доказать, что
- открыто, а
- замкнуто.
2.27 а) Построить на
топологии, индуцированные естественной
топологией на прямой, топологией
Зарисского, топологией Зоргенфрея.
Привести примеры ФСО для них.
б) Доказать, что для любых двух непересекающихся открытого и замкнутого множеств замыкание одного множества не пересекается с замыканием другого множества.
2.28 а) Построить ФСО
топологии на
,
индуцированной на нём топологией
Зарисского на
.
б) Показать, что пересечение конечного числа замкнутых множеств является замкнутым множеством.
2.29 а) Построить ФСО
топологии на
,
индуцированной на нём топологией
стрелки.
б) Показать, что
множество
открыто тогда и только тогда в пространстве
,
когда
.
-
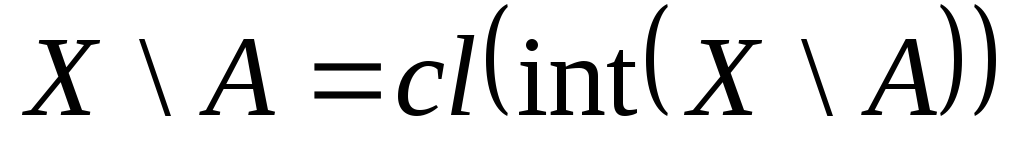а) Описать топологию на множестве
,
индуцированной естественной топологией,
топологиями Зарисского, Зоргенфрея.
Указать примеры ФСО для них.
б) пусть множество
открыто и
.
Доказать, что
.
-
Найти внутренность, замыкание, границу и внешность множеств
,
,
из
в естественной топологии, топологии
Зоргенфрея, дискретной топологии,
антидискретной топологии, топологии
Зарисского, топологии стрелки:
3.01
3.02
3.03
3.04
З.05
3.06
3.07
3.08
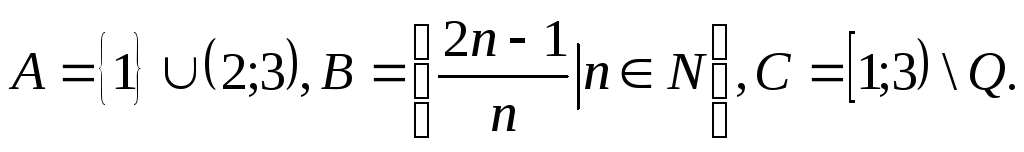
3.09
3.10
3.11
3.12
3.13
3.14
3.15
3.16
3.17
3.18
3.19
3.20
3.21
3.22
3.23
3.24
3.25
3.26
3.27
3.28
3.29
3.30
4.01 Показать, что
.
4.02 Доказать, что
множество
открыто тогда и только тогда, когда
4.03 Доказать, что если
,
то
.
4.04 Показать, что
.
4.05 Доказать, что для
любых подмножеств
и
пространства
справедливо
4.06 Доказать, что для
любых подмножеств
и
пространства
справедливо
4.07 Доказать, что для
любых подмножеств
и
пространства
справедливо
4.08 Доказать, что для
любых подмножеств
и
пространства
справедливо
4.09 Доказать, что для
любого
граница
есть замкнутое множество.
4.10 Доказать, что
множество
замкнуто тогда и только тогда, когда
.
4.11 Доказать, что для
любого
,
.
4.12 Доказать, что для
любого
,.
.
4.13 Доказать, что если
,
то
.
4.14 Доказать, что
,
для любого множества
.
4.15 Доказать, что
,
для любого множества
4.16 Показать, что
.
4.17 Доказать, что
множество
открыто тогда и только тогда, когда
4.18 Доказать, что если
,
то
.
4.19 Показать, что
.
4.20 Пусть
подпространство в топологическом
пространстве
.
Доказать, что множество
замкнуто в
тогда и только тогда, когда
является пересечением некоторого
замкнутого множества из
с
.
4.21 Доказать, что если
открытое множество в
,
то любое открытое множество в
открыто и в
.
4.22 Показать, что пересечение любого семейства замкнутых множеств является замкнутым множеством.
-
Доказать, что объединение конечного семейства замкнутых множеств является замкнутым множеством.
4.24 Доказать, что внутренность замкнутого множества есть канонически открытое множество.
4.25 Доказать, что пересечение двух канонически открытых множеств есть канонически открытое множество.
4.26 Доказать, что объединение двух канонически открытых множеств может не быть канонически открытым множеством.
4.27 Доказать, что
множество
замкнуто тогда и только тогда, когда
его дополнение канонически открыто.
-
Доказать, что для канонически открытых множеств
и
включение
имеет место в том и только в том случае,
если
.
4.29 Доказать, что
,
для любых множеств
и
.
4.30 Доказать, что
,
для любых множеств
и
.