
ЗАДАНИЕ 5.
АКСИОМЫ СЧЁТНОСТИ И ОТДЕЛИМОСТИ.
Основные понятия и определения.
Счётность.
Два множества
называются равномощными, если
существует биекция одного из них на
другое. Множества, равномощные некоторому
подмножеству множества
![]() натуральных
чисел, называются счетными. Иногда
так называют только бесконечные счетные
множества, т.е. только множества,
равномощные всему
натуральных
чисел, называются счетными. Иногда
так называют только бесконечные счетные
множества, т.е. только множества,
равномощные всему
![]() ,
а все конечные множества называют не
более чем счетными.
,
а все конечные множества называют не
более чем счетными.
Множество
![]() называется всюду плотным в
топологическом пространстве
называется всюду плотным в
топологическом пространстве
![]() ,
если
,
если
![]() .
.
Множество
![]() называется нигде не плотным в
топологическом пространстве
называется нигде не плотным в
топологическом пространстве
![]() ,
если
,
если
![]() .
.
Топологическое пространство называется сепарабельным, если оно содержит счётное всюду плотное подмножество.
Топологическое пространство удовлетворяет первой аксиоме счетности, если любая его точка имеет конечную или счетную ФСО.
Говорят, что топологическое пространство удовлетворяет второй аксиоме счетности, если оно имеет счетную или конечную базу топологии.
Пусть
![]() - семейство подмножеств топологического
пространства
- семейство подмножеств топологического
пространства
![]() и
каждое непустое открытое множество
содержит некоторый элемент семейства
и
каждое непустое открытое множество
содержит некоторый элемент семейства
![]() в качестве непустого подмножества, то
говорят, что
в качестве непустого подмножества, то
говорят, что
![]() плотно в
плотно в
![]() .
Плотная в
.
Плотная в
![]() система открытых множеств называется
система открытых множеств называется
![]() -
базой пространства
-
базой пространства
![]() .
.
Пространство называется нульмерным, если множества, одновременно открытые и замкнутые в нем, составляют его базу.
Пусть
![]() - подмножество топологического
пространства
- подмножество топологического
пространства
![]() .
Совокупность пределов всевозможных
последовательностей точек множества
.
Совокупность пределов всевозможных
последовательностей точек множества
![]() называется секвенциальным
замыканием этого множества. Мы
будем обозначать его
называется секвенциальным
замыканием этого множества. Мы
будем обозначать его
![]() .
.
Говорят,
что отображение
![]() секвенциально
непрерывно, если для любой точки
секвенциально
непрерывно, если для любой точки
![]() и для любой последовательности
и для любой последовательности
![]() точек пространства
точек пространства
![]() ,
стремящейся к
,
стремящейся к
![]() ,
последовательность
,
последовательность
![]() стремится к
стремится к
![]() .
.
Точка
![]() называется
изолированной в топологическом
пространстве
называется
изолированной в топологическом
пространстве
![]() ,
если одноточечное множество
,
если одноточечное множество
![]() одновременно открыто и замкнуто.
одновременно открыто и замкнуто.
Топологическое пространство называется нульмерным, если множества, одновременно открытые и замкнутые в нём, составляют его базу.
Примеры.
-
Множества
 и
и
 всюду плотны в пространстве
всюду плотны в пространстве
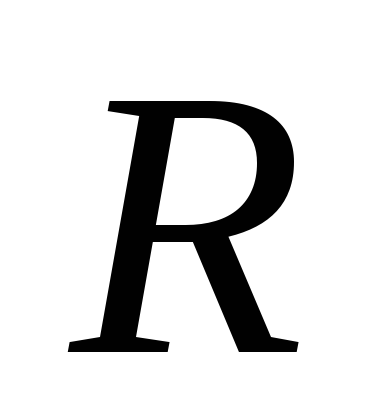 .
Так как множество
.
Так как множество
 счетно, то
счетно, то
 сепарабельно.
сепарабельно. -
Прямая, плоская кривая второго порядка, а также их подмножества являются нигде не плотными множествами на плоскости
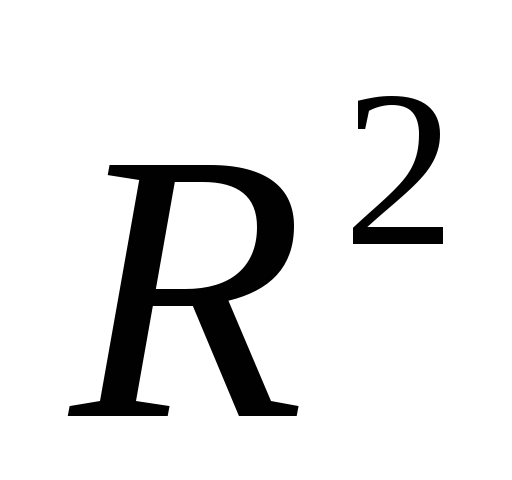
-
Прямая, плоскость, поверхность второго порядка, а также их любые подмножества - нигде не плотные множества в пространстве
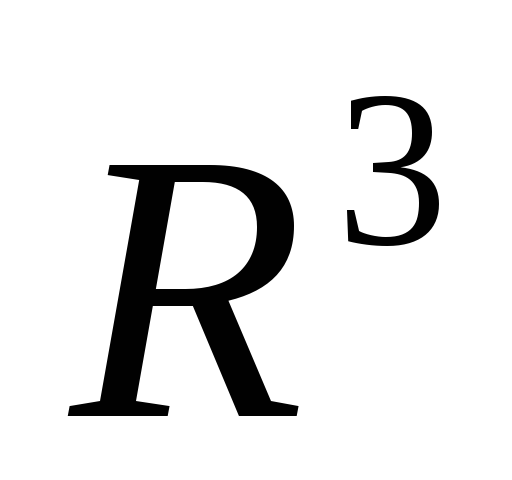 .
. -
Любое метризуемое пространство
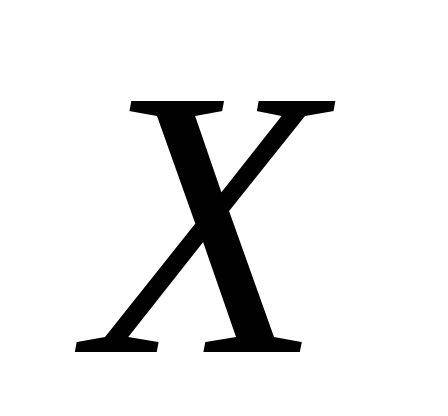 удовлетворяет
первой аксиоме счетности. Действительно,
зафиксировав некоторую метрику
удовлетворяет
первой аксиоме счетности. Действительно,
зафиксировав некоторую метрику
 ,
порождающую топологию, можно каждой
точке
,
порождающую топологию, можно каждой
точке
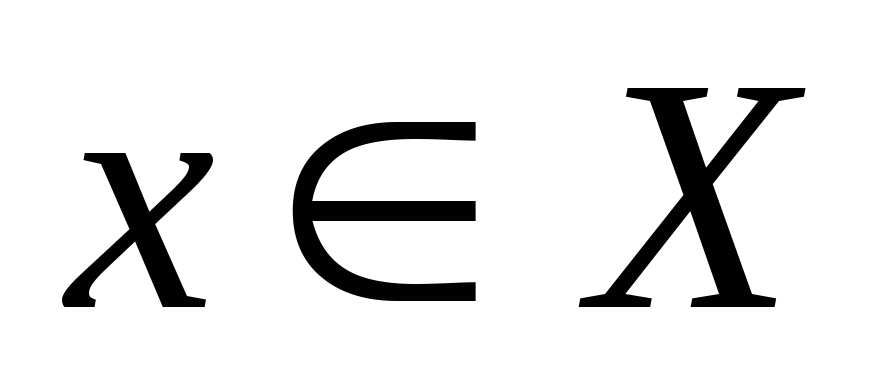 поставить в соответствие локальную
базу в этой точке:
поставить в соответствие локальную
базу в этой точке:
 .
. -
Топологическое пространство, даже метризуемое, может не обладать счетной базой. Действительно, пусть
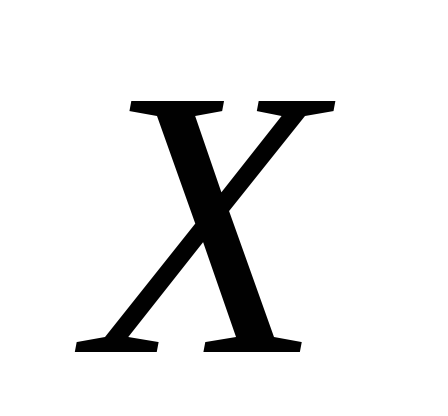 -
дискретное пространство несчетной
мощности (например, в качестве множества
-
дискретное пространство несчетной
мощности (например, в качестве множества
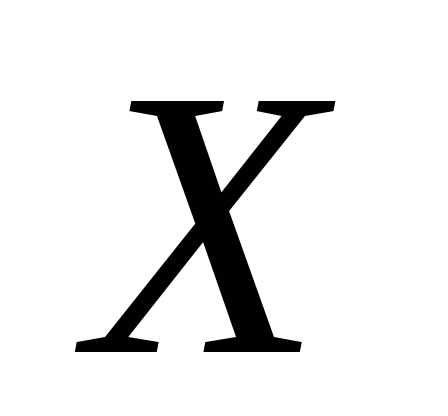 возьмем
возьмем
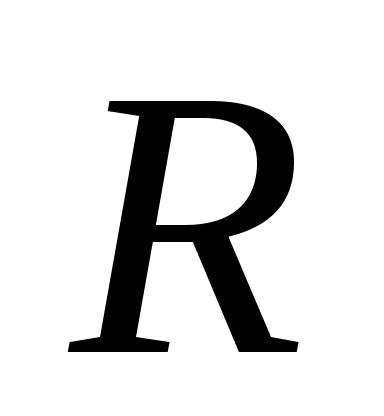 ),
),
 -
произвольная база дискретной топологии
-
произвольная база дискретной топологии
 .
Любое одноточечное множество
.
Любое одноточечное множество
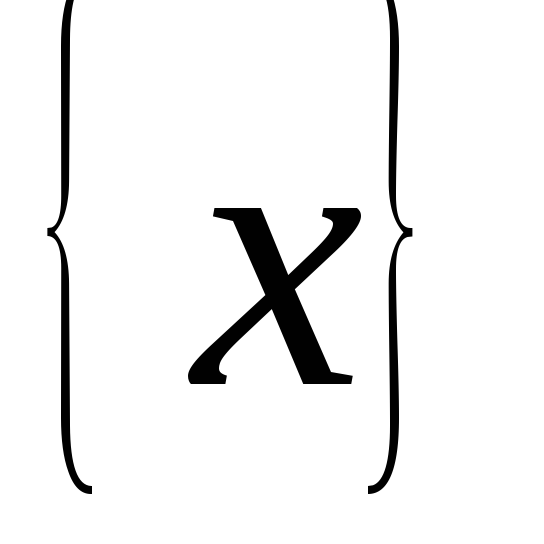 открыто
и, следовательно, представимо в виде
объединения некоторых элементов базы
открыто
и, следовательно, представимо в виде
объединения некоторых элементов базы
 .
Но поскольку множество
.
Но поскольку множество
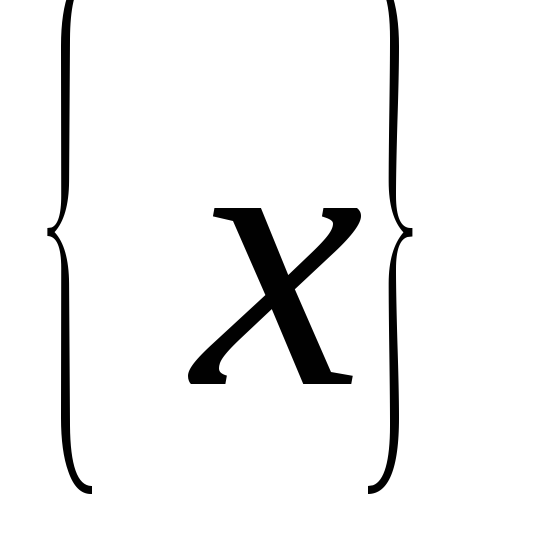 состоит из одной единственной точки,
оно само является элементом базы,
поэтому
состоит из одной единственной точки,
оно само является элементом базы,
поэтому  .
Таким образом, мощность базы
.
Таким образом, мощность базы
 не меньше мощности пространства
не меньше мощности пространства
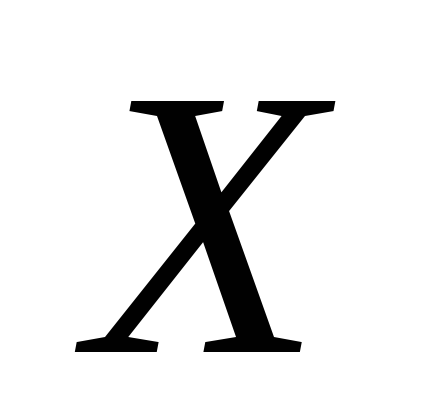 .
.
Основные теоремы
Теорема 40. Всякое метризуемое топологическое пространство есть пространство с первой аксиомой счетности.
Теорема
41. Множество
![]() нигде
не плотно тогда и только тогда, когда в
любом непустом открытом множестве
нигде
не плотно тогда и только тогда, когда в
любом непустом открытом множестве
![]() можно
указать непустое открытое множество
можно
указать непустое открытое множество
![]() ,
что
,
что
![]() .
.
Теорема
42. Множество
![]() нигде
не плотно тогда и только тогда, когда
всюду плотно множество
нигде
не плотно тогда и только тогда, когда
всюду плотно множество
![]() .
.
Теорема
43. Пусть
![]() -
топологическое пространство с первой
аксиомой счетности. Точка
-
топологическое пространство с первой
аксиомой счетности. Точка
![]() будет являться предельной точкой для
будет являться предельной точкой для
![]() тогда и только тогда, когда найдется
последовательность точек в
тогда и только тогда, когда найдется
последовательность точек в
![]() ,
сходящихся к
,
сходящихся к
![]() .
.
Теорема
44. Если пространство
![]() имеет счётную базу, (вторая аксиома
счетности) то оно сепарабельно.
имеет счётную базу, (вторая аксиома
счетности) то оно сепарабельно.
Теорема 45. (Обратная) Метрическое сепарабельное пространство удовлетворяет второй аксиоме счетности.
Таким образом, для метрических пространств сепарабельность равносильна второй аксиоме счетности.
Теорема 46. Непрерывный образ сепарабельного пространства сепарабелен.
Теорема 47. (Линделефа) Из всякого покрытия пространства, удовлетворяющего второй аксиоме счетности, открытыми множествами можно выделить счетный набор множеств, также являющийся покрытием.
Теорема 48. Из второй аксиомы счетности следует первая.
Теорема
49. Если пространство
![]() удовлетворяет первой аксиоме счетности,
то для любого
удовлетворяет первой аксиоме счетности,
то для любого
![]() верно
верно
![]() .
.
Теорема 50. Всякое непрерывное отображение секвенциально непрерывно.
Теорема 51. Прообраз секвенциально замкнутого множества при секвенциально непрерывном отображении секвенциально замкнут.
Теорема
52. Если пространство
![]() удовлетворяет первой аксиоме счетности,
то любое
удовлетворяет первой аксиоме счетности,
то любое
секвенциально
непрерывное отображение
![]() непрерывно.
непрерывно.
Теорема
53. (Брауэра) Пусть
![]() - семейство замкнутых множеств
пространства, обладающего счётной
базой, и пусть для любой убывающей
последовательности
- семейство замкнутых множеств
пространства, обладающего счётной
базой, и пусть для любой убывающей
последовательности
![]() множеств, принадлежащих семейству,
пересечение
множеств, принадлежащих семейству,
пересечение
![]()
![]() тоже принадлежит семейству. Тогда в
этом семействе есть множество, никакое
собственное
тоже принадлежит семейству. Тогда в
этом семействе есть множество, никакое
собственное
подмножество которого не принадлежит семейству.
