14

ЛАБОРАТОРНАЯ РАБОТА 6.

СВЯЗНОСТЬ И КОМПАКТНОСТЬ.

Основные понятия и определения.

Связность.

Топологическое пространство называется связным, если любое его подмножество, открытое и замкнутое одновременно, либо пусто, либо совпадает со всем пространством , т.е. нельзя представить в виде объединения никаких непустых открытых, дизъюнктивных подмножеств.

Подмножество топологического пространства называется связным в , если оно является связным топологическим подпространством с индуцированной топологией пространства .

Разбиением множества называется его покрытие попарно непересекающимися множествами; разбить множество – значит построить его разбиение.

Компонентой связности пространства называется всякое его связное подмножество, не содержащееся ни в каком (строго) большем связном подмножестве пространства .

Пусть - топологическое пространство, . Наибольшее связное подмножество, содержащее точку называется компонентой связности пространства , определенной точкой .

Компоненты связности пространства называются также связными компонентами или просто компонентами.

Топологическое пространство называется вполне несвязным, если любая его компонента состоит из одной точки.

Путем в топологическом пространстве называется непрерывное отображение отрезка в . Началом пути называется точка , концом - точка . Говорят в этом случае, что путь соединяет с .

Постоянное отображение называется постоянным путем и обозначается , где . Если - путь, то обратным ему путем называется путь , определяемый формулой . Хотя обозначение , строго говоря, уже занято (обратным отображением), к недоразумениям эта двусмысленность не приводит, поскольку, когда речь идет о путях, обратные отображения, как правило, не рассматриваются.

Линейно связным множеством называют множество, любые две точки которого можно соединить непрерывной кривой.

Компонентой линейной связности топологического пространства называется любое его линейно связное подмножество, не содержащееся ни в каком строго большем линейно связном множестве.

Подмножество евклидова пространства называется связным посредством ломаных, если любые две точки из можно в соединить конечнозвенной ломаной.

Компактность.

Покрытием пространства называется любое семейство открытых множеств , такое, что .

Покрытия, являющиеся частями данного покрытия называются его подпокрытиями.

Топологическое пространство называется компактным, если из любого его покрытия можно выделить конечное подпокрытие. Множество называется компактным, если оно компактно как подпространство с индуцированной топологией.

Совокупность подмножеств некоторого множества называется центрированной, если пересечение любого конечного набора множеств этой совокупности не пусто.

Топологическое пространство называется локально-компактным, если каждая его точка обладает окрестностью с компактным замыканием.

Топологическое вложение пространства в компактное пространство называется компактификацией пространства , если его образ плотен в . Так же в этой ситуации называется и пространство .

Пусть - хаусдорфово пространство. Пусть - множество, получающееся из добавлением одной точки (которая, разумеется, не принадлежит ). Пусть - совокупность подмножеств множества , состоящая из множеств, открытых в , и из дополнений в компактных подмножеств пространства . Тогда является компактификацией пространства .

Пусть - локально компактное хаусдорфово пространство и - его хаусдорфова компактификация с одноточечным , тогда существует гомеоморфизм , тождественный на . Такое называется одноточечной компактификацией или компактификацией Александрова пространства .

Непрерывное отображение называется собственным, если прообраз любого компактного множества при отображении компактен.

Пусть и - хаусдорфовы пространства. Всякое отображение естественным образом продолжается до отображения , которое определяется формулой

Функция называется локально ограниченной, если для каждой точки существует такая окрестность и такое число , что при .

Пусть - топологическое пространство, - некоторое свойство его подмножеств. Назовем - аддитивным, если объединение любого конечного набора множеств, обладающих свойством , так же обладает этим свойством. Скажем, что локально обладает свойством , если любая его точка имеет окрестность, обладающую этим свойством.

Точка называется точкой накопления множества , если любая ее окрестность содержит бесконечное число точек этого множества.

Примеры.

1. Множество несвязно, так как, зафиксировав любое иррациональное число , множество можно представить в следующем виде: , где ; .

2. Пространство связно для любого . Действительно, любые две точки можно соединить в пространстве однозвенной связной цепочкой, которой является отрезок .

3. Кольцо , где , связно, поскольку любые две точки можно соединить в кольце некоторой ломаной линией.

4. Понятие связности используется при доказательстве негомеоморфности некоторых

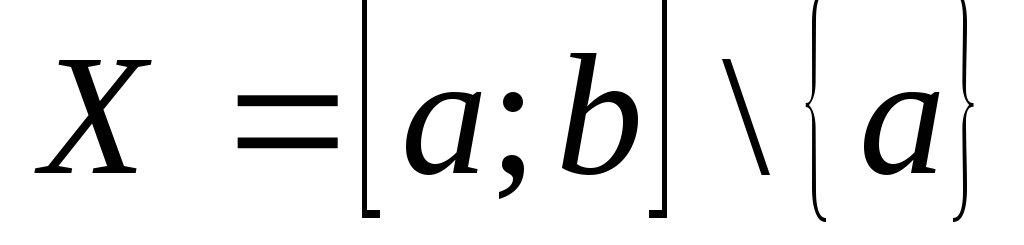топологических пространств. Покажем, например, что отрезок и интервал не гомеоморфны. Предположим противное. Допустим, что существует гомеоморфизм . Выколем точку и соответствующую ей точку . Полученные таким образом множества и 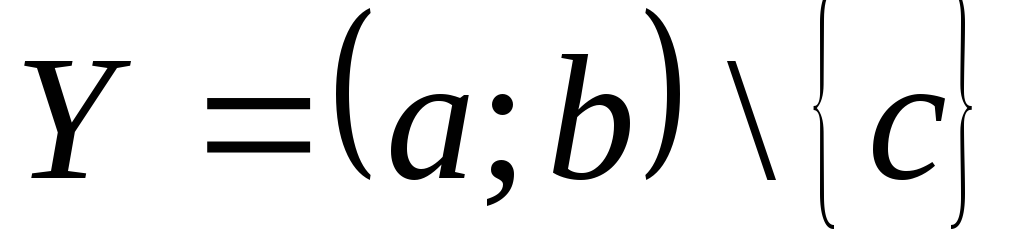тоже гомеоморфны. Но связно, а распадается на две связные компоненты. Получили противоречие.

5. Окружность линейно связна, поскольку ее можно представить в виде образа при непрерывном отображении , .

6. Лист Мебиуса и бутылка Клейна линейно связны, поскольку они представимы в виде образа при непрерывном отображении факторизуемого прямоугольника, который является линейно связным.

7. Отрезок линейно связен.

8. Евклидово пространство любой размерности линейно связно.

9. Сфера размерности линейно связна.

10. Рассмотрим с естественной топологией. Множество

есть пример связного, но не линейно связного топологического пространства.

11. Бесконечное дискретное пространство не компактно. Действительно, из покрытия нельзя выделить конечное подпокрытие.

12. Интервал не компактен. Чтобы убедиться в этом, достаточно рассмотреть

покрытия .

13. Пусть - метрическое пространство с метрикой . Множество называют

ограниченным, если найдется шар , где , такой, что .

В противном случае множество называют неограниченным. Покажем, что никакое неограниченное множество не может быть компактным. Для этого достаточно зафиксировать некоторую точку и рассмотреть семейство шаров . Очевидно, что - покрытие множества (и даже всего пространства ), из которого нельзя выделить конечное подпокрытие.

14. Любое конечное множество компактно.