119

Глава 11. Реакция технических систем на случайное воздействие

Случайными могут быть начальное состояние системы, входное воздействие в виде случайного процесса, оператор системы, структура системы. Ограничимся рассмотрением только второго случая, дополнительно положив, что оператор системы линеен, а входное воздействие стационарно.

11.1. Импульсная переходная (весовая) функция

Так называется реакция системы на единичную импульсную функцию - функцию Дирака

Кроме того

Обозначим A_t - оператор системы и g(t) - импульсную переходную функцию:

Сначала рассмотрим вспомогательное соотношение.

Здесь  - бесконечно малая величина, следовательно, по теореме о среднем

Теперь для реакции y(t) системы на воздействие x(t) получим

(11.1)

Рассмотрим пример. Оператор системы представляет собой обыкновенное дифференциальное уравнение первого порядка

Решение этого уравнения при начальных условиях имеет вид

где

Выполнив необходимые операции, находим импульсную переходную функцию

Если отсчет времени начинать с момента приложения к системе импульса и обозначить  = t -  , то

На рис. 11.1 изображен график этой функции.

Рис. 11.1.

Учтем теперь в формуле (11.1) , как и в примере, что реакция системы не может предшествовать воздействию, и сделаем подстановку  = t - . Теперь получим

(11.2)

Это интеграл по всей возможной предыстории системы.

11.2. Передаточная функция

Передаточной функцией называется отношение реакции системы к воздействию, имеющему вид гармонической функции.

Здесь p комплексный параметр.

Используя (11.2), находим, что реакция

(11.3)

Значит передаточная функция - это изображение по Лапласу импульсной переходной функции. Положим p = i, тогда получим частотную характеристику

Здесь присутствуют амплитудно- и фазочастотная характеристики.

Кроме прямого преобразования (11.3) существует и обратное. Оба преобразования записаны ниже в виде пары преобразований Фурье.

(11.4)

Продолжим ранее начатый пример.

Соответствующая частотная характеристика

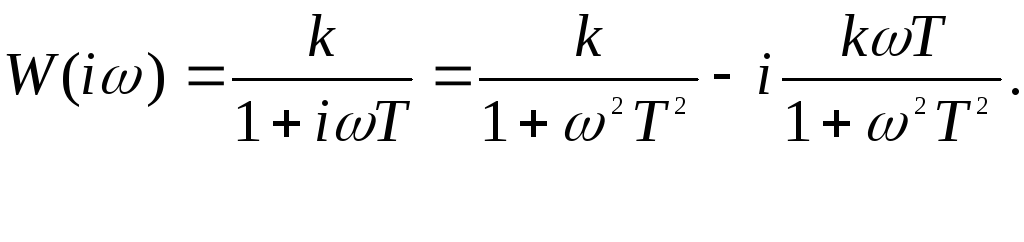
11.3. Корреляционная функция

Сначала определим математическое ожидание реакции системы, учитывая, что оператор системы линеен, а воздействующий на систему случайный процесс стационарен.

Центрирование реакции дает

Следовательно, корреляционная функция реакции системы такова.

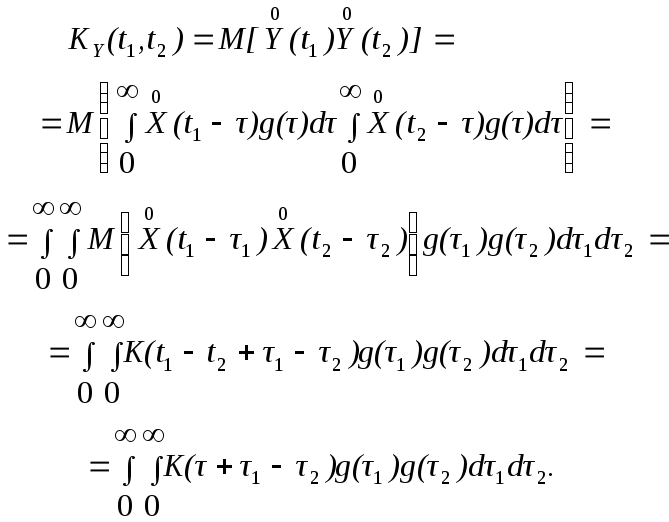
Итак,

11.4. Спектральная плотность реакции системы

Определим спектральную плотность при помощи соотношения

Найдем взаимосвязь между спектральными плотностями воздействия на систему и ее реакции.

Последний интеграл в этом выражении есть частотная характеристика системы, второй - комплексно сопряженное с ней выражение, а первый множитель в подынтегральном выражении - спектральная плотность входного воздействия. Таким образом, получаем следующие результаты.

Продолжим пример.

Квадрат модуля передаточной функции:

Спектр белого шума:

Спектр реакции системы:

Дисперсия реакции системы:

11.5. Горизонтальный полет крылатой ракеты в турбулентной атмосфере

Рассмотрим задачу при следующих допущениях.

1) Невозмущенное движение ракеты – плоское, горизонтальное с постоянной скоростью.

2) Турбулентность атмосферы стационарна, изотропна и описывается случайной функцией с нормальным распределением.

3) Уравнения возмущенного движения допускают линеаризацию.

Линеаризованные уравнения возмущенного продольного движения ракеты имеют вид [11]:

(11. 5)

Уравнения записаны для следующих переменных:

V - приращение скорости полета;

 - приращение угла тангажа;

Θ - приращение угла наклона траектории к горизонту;

δ - приращение угла отклонения рулей высоты;

α - приращение угла атаки;

y - приращение высоты полета;

u- пульсационная составляющая скорости ветра.

Звездочкой отмечена скорость невозмущенного полета.

Первое и пятое уравнения являются уравнениями движения центра масс ракеты в проекциях на касательную и нормаль к траектории. Второе уравнение описывает вращательное движение ракеты вокруг центра масс. Четвертое уравнение - уравнение автопилота. l₁...l₄- его передаточные числа. Третье уравнение - кинематическое. Это связь между углами тангажа, атаки, наклона траектории и дополнительного угла атаки, вызванного турбулентными пульсациями.

Динамические коэффициенты, входящие в уравнения таковы. Все они выражены через параметры невозмущенного движения.

Кроме ранее расшифрованных здесь использованы обозначения:

M- масса ракеты;

M_Z - аэродинамический момент относительно поперечной оси;

I_Z - момент инерции относительно поперечной оси;

P - тяга двигательной установки воздушно-реактивного двигателя ракеты;

g - ускорение свободного падения.

Верхний индекс обозначает производную по соответствующей переменной. Производные равны:

Здесь C_X, C_Y, m_Z - аэродинамические коэффициенты,q- скоростной напор, G_В - расход воздуха в двигателе. Остальные производные считаются равными нулю.

После преобразования по Лапласу уравнения возмущенного движения запишутся в операторной форме в виде системы алгебраических уравнений. Матрица, составленная из коэффициентов при изображениях неизвестных, имеет вид. Коэффициенты комплексные. Их действительные и мнимые части разделены запятыми.

.

Матрица правых частей уравнений

В матрице A p- комплексный параметр преобразования Лапласа. Решение системы уравнений дает следующие передаточные функции:

(11.6)