3.2.4. Анализ результатов испытаний

Завершающим этапом испытаний по полному или дробному факторному плану является статистический анализ полученных данных, который включает: оценку воспроизводимости результатов испытаний; оценку значимости коэффициентов регрессии и уточ­нение вида модели; проверку адекватности модели.

Целью проверки воспроизводимости является установление однородности результатов испытаний, проводимых на различных уровнях . В ходе опытно-конструкторских ра­бот при проведении лабораторных и стендовых испытаний обычно используется освоенная аппаратура, обеспечивающая стабиль­ность условий. Поэтому предварительное заключение относительно воспроизводимости ожидаемых результатов часто может быть сделано до начала испытаний. При необходимости проверки воспроизводимости содержание задачи совпадает с задачей провер­ки гипотезы о стабильности условий испытаний. Пусть результаты испытаний представлены, как показано в табл. 2.8.

Проверке подлежит гипотеза , где – количество строк матрицы планирования. Условием проверки гипо­тезы является наличие параллельных опытов в каждой из строк.

Тогда в каждой строке могут быть вычислены

; , ,

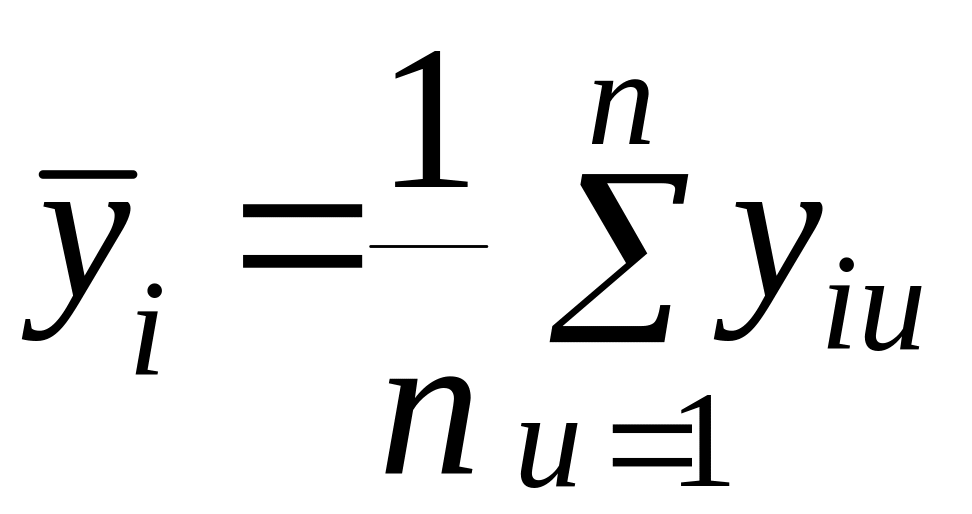где – количество повторных испытаний.

Таблица 2.8

Номер опыта	План испытаний					Результаты испытаний				Вычисляемые оценки
1	+	–	–	. . .	+			. . .
2	+	–	+	. . .	+			. . .
								. . .
	+	–	+	. . .	–			. . .

Для проверки гипотезы можно воспользоваться критериями Кохрена или Бартлетта. Если , расчетное значе­ние статистики критерия Кохрена определяется по формуле (1.49) и гипотеза принимается, если , где , . Если дисперсии однородны (принята гипоте­за ), то дисперсия опыта (или, что то же самое, дисперсия вос­производимости) подсчитывается по зависимости

, (3.2.11)

где знаменатель характеризует число степеней свободы . В общем случае, подсчитывается как среднее взве­шенное значение

. (3.2.12)

Проверка значимости коэффициентов регрес­сии позволяет лучше осмыслить математическое описание про­цесса, а также уточнить вид модели путем отсеивания факторов, слабо влияющих на значение выходного параметра. Проверка зна­чимости каждого из коэффициентов производится независимо, с помощью проверки гипотезы 0 по -критерию. Расчетные значения статистики критерия можно определить по соотношению

. (3.2.13)

Если , то коэффициент является значимым и соответствующий фактор оказывает существенное влияние на величину . Статистическая незначимость может быть вызвана следующими причинами:

• интервал варьирования был выбран слишком малым;

• уровень начального режима по фактору оказался близок к точке частного экстремума ;

• велика ошибка опыта из-за влияния неуправляемых и неконтролируемых факторов;

• данный фактор (совокупность факторов) не оказывают за­метного влияния на величину выходного параметра.

Поскольку план ортогонален и коэффициенты оцениваются не­зависимо друг от друга, оказавшиеся незначимыми коэффициен­ты могут быть отброшены без пересчета остальных.

Проверка адекватности заключается в подтвержде­нии предположения, что полученная математическая модель до­статочно верно описывает характер процесса. Формальное содержание гипотезы состоит в том, что предсказанные уравнением (расчетные) значения выходного параметра отклоняются от опытных на величину, не превышающую некоторый наперед за­данный уровень, и модель пригодна для обоснования инженерных решений. Для проверки гипотезы оценивается дисперсия адекват­ности

, . (3.2.14)

Если дисперсия адекватности не превышает дисперсии опыта , то есть основание полагать, что модель адекватно описывает процесс. Согласно п. 1.3 для проверки гипотезы о диспер­сиях используется -критерий. Статистика критерия

. (3.2.15)

Модель считается адекватной процессу, если , где , . Если ,то для получения адекватного описания необходимо увеличить порядок аппроксимирующего полинома. Очевидно, что проверка адекватности возмож­на лишь в том случае, если , то есть число разных испытаний превосходит количество включаемых в модель факторов.

Если гипотеза адекватности принимается, то модель может использоваться для управления процессом (при доводочных испы­таниях для определения значений факторов, при которых дости­гается экстремальное или заданное значение выходного парамет­ра). Незначимые коэффициенты могут быть отброшены, однако при этом необходима основанная на анализе физической сущ­ности явления уверенность, что эти факторы не влияют на выход­ной параметр. В противном случае следует стремиться продолжить испытания (расширив, если позволяют технические возможности, по незначимым факторам).

Если модель неадекватна, возможны следующие решения: перейти к модели более высокого порядка (когда можно предпо­ложить, что опыты проводились в области, близкой к оптималь­ной); продолжить испытания, уменьшив интервал варьирования, или перенося центр плана в другую точку.

Рассмотрим примеры использования ДФП при организации ис­пытаний технических систем.

1. Планируются испытания двигателя на надежность при эксплуа­тации. В качестве основных эксплуатационных факторов выделе­ны: механические воздействия при транспортировании, воспроизво­димые на вибростенде температура и влажность воздуха , имитируемые попеременным термостатированием и выдержкой в термобарокамере; старение при хранении, достигаемое проведени­ем ускоренных испытаний узлов двигателя ; излучение и прогрев эле­ментов с помощью секционных термобарокамер с использова­нием электронагревательных приборов и холодильной установки, В качестве выходного параметра оценивалась величина давления в блоке цилиндров двигателя . Для испытаний выделялось двигателей. Поскольку для полного учета всех факторов (при числе уровней ) необходимо образца, было принято решение применить ДФП , причем , . Тогда обобщенный определяющий контраст . Получаемая в этом случае математическая

модель принимает вид

Поскольку реализация плана возможна при , остав­шиеся четыре образца использовались для проведения контроль­ной серии испытаний. План испытаний показан в табл. 2.9.

2. Планируются испытания двигателя, проводимые с целью эмпири­ческого определения коэффициента усиления, величина которого в общем виде представляется как , где – изме­нение -того регулируемого выходного параметра двигателя, – изменение регулирующего параметра по -тому каналу регулирования. Исполнительными органами систем регулирования являются регуляторы расхода, регуляторы давления, дроссели. Величина обычно включается в ТЗ на раз­работку.

Таблица 2.9

Номер опыта						Номер опыта
1	–	–	–	–	+	7	–	+	+	–	+
2	+	–	–	+	+	8	+	+	+	+	+
3	–	+	–	+	–	9	+	+	+	+	+
4	+	+	–	–	–	10	0	0	0	0	0
5	–	–	+	+	–	11	–	–	–	–	+
6	+	–	+	–	–	12	–	+	–	+	–

Из практики опытной отработки известно, что расчетные значения обычно не подтверждаются в ходе испытаний. Поэто­му возникает потребность настройки регулирующих органов с по­следующей опытной проверкой. Для обеспечения эффективности организации работ по определению и настройке коэффициентов усиления по каналам регулирования двигателя находят примене­ние полные и дробные факторные планы. Рассмотрим случай, в котором для проведения испытаний реализуется ПФП при числе испытаний (табл. 2.10). В каждом испытании значения фак­торов и ( и ) определяют крайние положения органов в выбранной области изменения этих факторов. Матрица планиро­вания и полученные из опыта результаты представлены в табл. 2.10. В нижней строке таблицы приводятся вычисленные по формуле (3.2.8) значения коэффициентов

Таблица 2.10

Режим	План				Результаты испытаний
1	+	–	–	+	0,7166	0,6769	0,7166	0,5785	0,6721	0,6939
2	+	–	+	–	0,8100	0,8100	0,8700	0,7545	0,8111	0,7893
3	+	+	–	–	0,6615	0,6076	0,5250	0,6071	0,6003	0,6221
4	+	+	+	+	0,6071	0,5533	0,4941	0,5375	0,5480	0,5263
	0,6578	– 0,0837	0,0216	– 0,0478

Рассмотрим порядок статистического анализа результатов ис­пытаний. Для проверки условия воспроизводимости по формуле (3.2.11) определим

; ; ; .

Затем вычислим расчетное значение стати­стики критерия Кохрена:

Из табл. П.2.7---------? при уровне значимости и числе степеней свободы , находим . Поскольку , принимается гипотеза об однородности данных (вос­производимости результатов испытаний). Следовательно, диспер­сия испытаний может быть определена по всем испытаниям со­гласно зависимости (3.2.12):

.

Из (3.2.9) видно, что погрешность оценивания

.

Для проверки значимости коэффициентов и уточнения вида модели вычислим расчетные значения статистики -критерия по формуле (3.2.13):

; ; .

Из таблицы Приложения при и получим . Следовательно, для и имеет место и эти коэффициенты значимо отличаются от нуля. Поскольку коэффициент оказался незначимым. Поэтому фак­тор из дальнейшего рассмотрения исключаем. Уточненная модель принимает вид

Для проверки адекватности модели определим предсказанные этой моделью значения ; ; ; . Согласно зависимости (3.2.14) мера неадекватности модели оценивается дисперсией

.

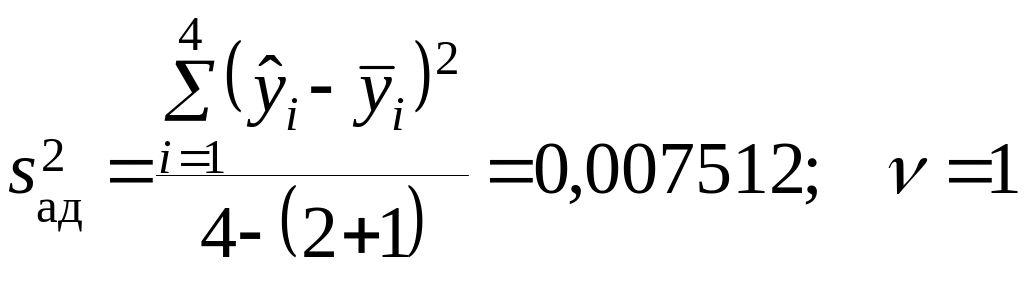Тогда определяемое по (3.2.15) расчетное значение статистики критерия

.

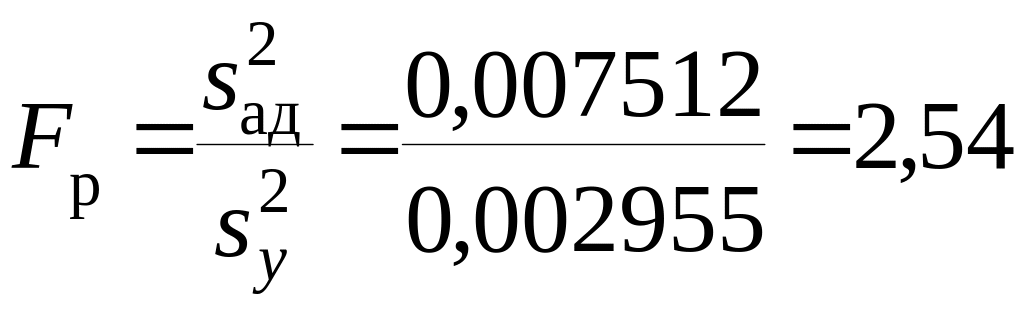Из табл. П.2.6------------? при , , находим , что позволяет принять гипотезу об адекватности модели изучаемому процессу и использовать ее в дальнейшем для настройки двигателя.