
- •1. Вектордың анықтамасы. Тең векторлардың анықтамасы.
- •2. Векторларды қосу амалының анықтамасы. Векторларды қосу амалының қасиеттерін дәлелдеу.
- •3. Векторды санға көбейту амалының анықтамасы. Векторды санға көбейту амалының қасиеттерін дәлелдеу.
- •4. Сызықты тәуелді векторлар жүйесінің анықтамасы. Коллениар және компланар векторлардың сызықтық тәуелділігін көрсету.
- •5. Сызықты тәуелді векторлар жүйесінің қасиеттерін дәлелдеу.
- •6. Сызықтық тәуелсіз векторлар жүйесінің анықтамасы. Мысалдар. Сызықтық тәуелсіз векторлар жүйесінің қасиеттері.
- •11.Кеңістіктегі акж
- •12. Кеңістіктегі акж (декарттық тікбұрышты координаттар жүйесі )(рис. 4.4) (Афиндик)
- •19.Векторлардың аралас көбейтіндісінің анықтамасы және геометриялық мағынасы.
- •20. Векторлардың аралас көбейтіндісінің қасиеттері мен есептеу формулалары:
- •21. Жазықтықтағы түзудің параметрлік,канондық,екі нүкте арқылы өтетін түзудің, кесінділермен берілген түзудің теңдеулерін қорытып шығару
- •28.Жазықтықтың параметрлік және үш нүкте арқылы өтетін теңдеуін қорытып шығару.
- •29.Жазықтықтың жалпы теңдеуін қорытып шығару.
- •30. Екі жазықтықтың өзара орналасуы туралы теореманы дәлелдеу.
- •34. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың есептеу формуласын қорытып шығару.
- •35. Кеңістіктегі екі түзудің өзара орналасуы.
- •36. Кеңістіктегі түзу мен жазықтықтың өзара орналасуы.
- •37. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыштың синусын есептеу формуласын қорытып шығару.
- •38. Кеңістікте нүктеден түзуге дейінгі арақашықтықтың есептеу формуласын қорытып шығару.
- •46, Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
- •47,Эллипс (канондық теңдеуін қорыту, фокалдық радиустарды есептеу, эксцентриситет, параметрлік теңдеу).
- •47,Эллипс
- •48,Гипербола
- •46,Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
- •1 Сурет 1
- •1 Сурет 2
- •52. Екінші ретті сызықтардың типтерге бөлініуі
- •53. Екінші ретті сызықтардың жалпы теңдеуінің инварианттары туралы теорема.
- •Екінші ретті сызықтардың центрі туралы теоремаларды дәлелдеу. Центрі бар және центрі жоқ қисықтар.
- •2. Гиперболалық параболоидтың канондық теңдеуі. Гиперболалық параболоидтың қималары.
- •64. Целиндтлік бет және оның қималары
- •65. Эллипстік параболоидтың канондық теңдеуін қорытып шығару. Эллипстік параболоидтың қималары.
- •67. Гиперболалық параболоидтың түзу сызықты жасаушалары.
- •68. Екінші ретті беттердің жалпы теңдеуі. Екінші ретті беттердің типтерге бөлінуі.
- •69. Екінші ретті беттердің жалпы теңдеуін 17 канондық теңдеуге келтіру.
- •70. Екінші ретті беттердің жалпы теңдеуінің инварианттары
21. Жазықтықтағы түзудің параметрлік,канондық,екі нүкте арқылы өтетін түзудің, кесінділермен берілген түзудің теңдеулерін қорытып шығару
 нүктесі
және a={l,m} бағыттаушы векторы арқылы
өтетін түзудін параметрлік тендеуі
мынадай түрде болады x=
нүктесі
және a={l,m} бағыттаушы векторы арқылы
өтетін түзудін параметрлік тендеуі
мынадай түрде болады x= y=
y=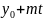
Дәлелдеуі;M(x,y)-жазықтықтың
кез-келген нүктесі. M(x,y) нүктесі берілген
жазықтықта жатады сонда және тек сонда
ғана егер
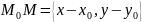 және a={l,m} векторлары коллинеар болса
сонда
және a={l,m} векторлары коллинеар болса
сонда
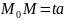
Ал
координаталық түрде x-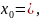 y-
y-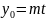 бұдан x=
y=
.
бұдан x=
y=
.
Егер
параметрлік тендеуді
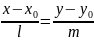 түрінде жазсақ ол канондық тендеу деп
аталады.
түрінде жазсақ ол канондық тендеу деп
аталады.
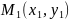 және
және
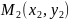 нүктелері берілген екі нүкте арқылы
өтетін түзудің тендеуі төмендегідей
түрде жазылады
нүктелері берілген екі нүкте арқылы
өтетін түзудің тендеуі төмендегідей
түрде жазылады
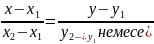
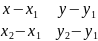
Дәлелдеуі; ;
;
Кесінділермен берілген түзудін тендеуі
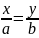
22.Жазықтықтағы
түзудің жалпы түзудің теңдеуін қорытып
шығару:Ax+By+Cz+D=0,A2
+B2
+C2≠0,A≠0
x=(-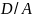 )+u(-
)+u(-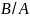 )+v(-
)+v(-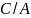 )
y=0+1*u+0*v z=0+0*u+1*v
)
y=0+1*u+0*v z=0+0*u+1*v
(·)(- ,0,0) (·)(- ,0,0) (·)(- ,0,,0)→||π
23.
Жазықтықтағы екі түзудің өзара орналасуы
туралы теореманы дәлелдеу.Теорема:
π1
:
A 1x+B
1y+C
1z+D1=0
π2
:
A 2x+B
2y+C
2z+D2=0
1)
π1
≡ π2↔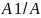 2
=
2
=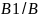 2
=
2
=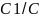 2
=
2
= 2
=λ
2)
π1||
π2↔
2
=
2
=
2
=
2
=λ
2)
π1||
π2↔
2
=
2
=
2
=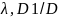 2
≠λ
3)
π1∩
π2↔
2
≠
2
≠
2
≠
λ ДӘлелдеу:жет.лік:
2
=
2
=
2
=
2
=λ
,
π1:
λ
A 2x+
λ
B 2y+
λ
C 2z+D2=0→
λ(A
2x+B
2y+C
2z+D2)=0
→
π1
≡ π2
Қажеттілік:
π1
≡ π2,
π1
||
a1b1
,
π2||a2b2,
a1=(-B1,A1,0),a2=(-B2,A2,0),b1=(-C1,0,A1),b2=(-C2,0,A2),
a1,b1
||
π2→1)A2·
(-B1)
+B2·A1+C2·0=0,
2
=
2
,
2)
A2·
(-C1)
+B2·0+C2·A1=0,
2
=
2
→
2
=
2
=
2
→
π1:
λ
A 2x+
λ
B 2y+
λ
C 2z+D2=0,
π2
:
A 2x+B
2y+C
2z+D2=0
,
π1:
π2→D1=λD2,
2
=λ
2
≠λ
3)
π1∩
π2↔
2
≠
2
≠
2
≠
λ ДӘлелдеу:жет.лік:
2
=
2
=
2
=
2
=λ
,
π1:
λ
A 2x+
λ
B 2y+
λ
C 2z+D2=0→
λ(A
2x+B
2y+C
2z+D2)=0
→
π1
≡ π2
Қажеттілік:
π1
≡ π2,
π1
||
a1b1
,
π2||a2b2,
a1=(-B1,A1,0),a2=(-B2,A2,0),b1=(-C1,0,A1),b2=(-C2,0,A2),
a1,b1
||
π2→1)A2·
(-B1)
+B2·A1+C2·0=0,
2
=
2
,
2)
A2·
(-C1)
+B2·0+C2·A1=0,
2
=
2
→
2
=
2
=
2
→
π1:
λ
A 2x+
λ
B 2y+
λ
C 2z+D2=0,
π2
:
A 2x+B
2y+C
2z+D2=0
,
π1:
π2→D1=λD2,
2
=λ
24.
Жартыжазықтықтар. Түзудің бас
векторы.π:Ax+By+Cz+D=0,(·)M(x,y,z)є
π,(·)M1(x1,y1,z1),(·)M2(x2,y2,z2)
єемес
π –ға,(M1M2,
(·)M)=
λ>0,
M1M2||MM2,
x=
X1+λx2/1+λ,y=
y1+λy2/1+λ,
z=z1+λz2/1+λ,A·(
X1+λx2/1+λ)+B
·(
y1+λy2/1+λ
)+C·(
z1+λz2/1+λ)+D=0,
A x1+B
y1+C
z1+D+λ(A
x2+B
y2+Cz2+D)=0,-λ=(
A x1+B
y1+C
z1+D)/(
A x2+B
y2+Cz2+D)<0→
Ax+By+Cz+D>0, Ax+By+Cz+D<0
Ан.ма: N=(A,B,C) векторы π жазықтағының бас векторы деп аталады
25. Екі тузу арасындағы бұрыш
 b
р1-дін бағыттаушы векторы
а,р2- дін бағыттаушы векторы b
b
р1-дін бағыттаушы векторы
а,р2- дін бағыттаушы векторы b
⎺a(x1,y1) ⎺b(x2,y2) cos α=(⎺a,⎺b)/│a│*│b│=(x1*x2+y1*y2)/


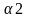
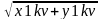 *
*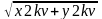
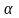 a
sinα=sin(α2-α1)=sinα2*cosα1-sinα1*cosα2=y2/│b│*x1/│a│-
a
sinα=sin(α2-α1)=sinα2*cosα1-sinα1*cosα2=y2/│b│*x1/│a│-
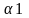 -y1/│a│*x2/│b│=(x1*y2-x2*y1)/
*
-y1/│a│*x2/│b│=(x1*y2-x2*y1)/
*
Tgα=sinα/cosα=(x1*y2-x2*y1)/(x1*x2+y1*y2)l;
А)P1:x=x1+l1*t; y=y1+m1t ⎺a1=(l1,m1)-бағ.векторы
Р2: x=x2+l2*t; y=y2+m2*t; ⎺b2=(l2,m2)-бағ.векторы
Tgα=(l1*m2-l2*m1)/(l1*l2+m1*m2)
Б)р1:A1x+B1y+C1=0 ⎺a1=(-B1;A1)
Р2: A2x+B2y+C2=0 ⎺a2=(-B2;A2)
Tgα=(-B1*A2+B2*A1)/(A1*A2+B1*B2)
B)p1:y=k1*x+b1; a1=(1;k1)
P2: y=k2*x+b2 ; a2(1;k2) tgα=(k2-k1)/(1+k2*k1)
26.; Жазықтықтағіы тузудің нормаль теңдеуін қорытып шығару.

y P ⎺OP⊥L e↑↑⎺OP e-бірлік демек ⎺OP-ның орты│ ⎺OP│=p⟶
l ⎺OP=р*⎺е ; cosα=x/│⎺e│⟶Xe ; ⎺e(cosα;sinα); ⎺ОМ=⎺r
n ⎺OM=⎺OP+⎺PM⟶⎺PM=⎺OM-⎺OP=⎺r- р*⎺е (*)Mтиісті l⟶⎺OP⊥
e M ⎺PM⟶⎺е ⊥ ⎺PM⟶⎺е ⊥(⎺r- р*⎺е )=0;( ⎺r- р*⎺е, ⎺е )=0⟶
O x (⎺r, ⎺е)-p(⎺e,⎺e)=(⎺r, ⎺е)-p=0⟶x*cosα+y*sinα-p=0
Жалпы
теңд:Ax+By+C=0,
M=1/±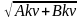 -нормалаушы
көбейткіш,
ж.тенд
*M⟶
-нормалаушы
көбейткіш,
ж.тенд
*M⟶
(Ax+By+C)/ ± =0
Жазықтықтағы екі түзудің параллель және перпендикуляр болу шарттары.
1)р1││р2⟶A1/A2=B1/B2;l1/l2=m1/m2,k1/k2=1; k1=k2
2)p1⊥p2⟶A1*A2+B1*B2=0; l1*l2+m1*m2=0,1+k1*k2=0⟶k2=-1/k1
27.Жазықтықтағы нүктеден түзуге дейінгі арақашықтық
n0 M0 M0(x0,y0) d:Ax+By+C=0 ⟦M0M1⟧⊥d,M1€d және ⎺n0-d түзу
нормальінің
орты болсын.Сонда ⎺M1M0=α⎺n0
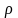 (M0,d)=│α│=
(M0,d)=│α│=

 M1 d
(*) │⎺n0*⎺M1M0│.
⎺n=A⎺i+B⎺j⟶⎺n0=(
A⎺i+B⎺j)/
(1)
M1 d
(*) │⎺n0*⎺M1M0│.
⎺n=A⎺i+B⎺j⟶⎺n0=(
A⎺i+B⎺j)/
(1)
⎺M1M0=(x0-x1)⎺i+(yo-y1)⎺j. (2) (1),(2)⟶ ⎺n0*⎺M1M0=1/
; (A(x0-x1)+B(yo-y1))=(Ax0+By0-(Ax1+By1)/ (3)
M1€d⟶Ax1+By1+C=0⟶-(Ax1+By1)=C (4)
(*),(3),(4)⟶ (M0,d)=│Ax0+By0+C│/
Жазықтықтағы түзудің координаталық осьтерге қатысты орналасуының дербес жағдайлары. Ах+Ву+С=0
1)C=0⟶ Ах+Ву=0 түрінде жазылады.бұған сәйкес түзу координаталардың бас нүктесін басып өтеді
2)B=0⟶Ax+C=0 түрінде жазылады,OY осьне парраллель түзуді анықтайдыc
3)A=0⟶ Ву+C=0 түрінде жазылады,OX осьне парраллель түзуді анықтайды
4)B=0,C=0⟶ X=0 түрінде жазылады. Да, OY осьн анықтайды
5)A=0,C=O ⟶Y=0 түрінде жазылады ДА, OX осьн анықтайды
