
- •1. Вектордың анықтамасы. Тең векторлардың анықтамасы.
- •2. Векторларды қосу амалының анықтамасы. Векторларды қосу амалының қасиеттерін дәлелдеу.
- •3. Векторды санға көбейту амалының анықтамасы. Векторды санға көбейту амалының қасиеттерін дәлелдеу.
- •4. Сызықты тәуелді векторлар жүйесінің анықтамасы. Коллениар және компланар векторлардың сызықтық тәуелділігін көрсету.
- •5. Сызықты тәуелді векторлар жүйесінің қасиеттерін дәлелдеу.
- •6. Сызықтық тәуелсіз векторлар жүйесінің анықтамасы. Мысалдар. Сызықтық тәуелсіз векторлар жүйесінің қасиеттері.
- •11.Кеңістіктегі акж
- •12. Кеңістіктегі акж (декарттық тікбұрышты координаттар жүйесі )(рис. 4.4) (Афиндик)
- •19.Векторлардың аралас көбейтіндісінің анықтамасы және геометриялық мағынасы.
- •20. Векторлардың аралас көбейтіндісінің қасиеттері мен есептеу формулалары:
- •21. Жазықтықтағы түзудің параметрлік,канондық,екі нүкте арқылы өтетін түзудің, кесінділермен берілген түзудің теңдеулерін қорытып шығару
- •28.Жазықтықтың параметрлік және үш нүкте арқылы өтетін теңдеуін қорытып шығару.
- •29.Жазықтықтың жалпы теңдеуін қорытып шығару.
- •30. Екі жазықтықтың өзара орналасуы туралы теореманы дәлелдеу.
- •34. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың есептеу формуласын қорытып шығару.
- •35. Кеңістіктегі екі түзудің өзара орналасуы.
- •36. Кеңістіктегі түзу мен жазықтықтың өзара орналасуы.
- •37. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыштың синусын есептеу формуласын қорытып шығару.
- •38. Кеңістікте нүктеден түзуге дейінгі арақашықтықтың есептеу формуласын қорытып шығару.
- •46, Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
- •47,Эллипс (канондық теңдеуін қорыту, фокалдық радиустарды есептеу, эксцентриситет, параметрлік теңдеу).
- •47,Эллипс
- •48,Гипербола
- •46,Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
- •1 Сурет 1
- •1 Сурет 2
- •52. Екінші ретті сызықтардың типтерге бөлініуі
- •53. Екінші ретті сызықтардың жалпы теңдеуінің инварианттары туралы теорема.
- •Екінші ретті сызықтардың центрі туралы теоремаларды дәлелдеу. Центрі бар және центрі жоқ қисықтар.
- •2. Гиперболалық параболоидтың канондық теңдеуі. Гиперболалық параболоидтың қималары.
- •64. Целиндтлік бет және оның қималары
- •65. Эллипстік параболоидтың канондық теңдеуін қорытып шығару. Эллипстік параболоидтың қималары.
- •67. Гиперболалық параболоидтың түзу сызықты жасаушалары.
- •68. Екінші ретті беттердің жалпы теңдеуі. Екінші ретті беттердің типтерге бөлінуі.
- •69. Екінші ретті беттердің жалпы теңдеуін 17 канондық теңдеуге келтіру.
- •70. Екінші ретті беттердің жалпы теңдеуінің инварианттары
11.Кеңістіктегі акж
Кеңістіктегі АКЖ деп бір жазықтықта жатпайтын,координаттар басы бірдей О(.)-де болатын,реттелген 3 координаттық осьтердің топтастыруын айтамыз.

Y
 -абцисс
осі
-абцисс
осі
 -ордината
осі
-ордината
осі
 -аппликата
осі
-аппликата
осі
О x
z
z R M(.)-ң координаттарын табу үшін,Ол нүктенің проекциясын қарастыру керек,АКЖ-да кез-келген екі координаттық ось арқ. координаттық жазықтық жүргізуге болады.


 XOY,YOZ,ZOX.
XOY,YOZ,ZOX.
M Прох(.)М(||YOZ)= (.)Р


 Проy(.)М(||ZOX)=
(.)Q
Проy(.)М(||ZOX)=
(.)Q
О y Проz(.)М(||XOY)= (.)R
Q
P P(x,00)
X Q(0,y,0)}=˃M(x,y,z)
R(0,0,z)
(x,y,z) кеңістіктегі М (.)-ң Афиндік координаталары д.а.
X=0˂=˃(.)М € YOZ X=0, Y=0˂=˃(.)М € OZ
Y=0˂=˃(.)М € XOZ Y=0, Z=0˂=˃(.)М € OX
Z=0˂=˃(.)М € XOY Z=0, X=0˂=˃(.)М € OY
OY,OZ, OX координаттық осьтерінде Е1,Е2,Е3 бірлік нүктелерін аламыз.
 1,
2,
3
векторлары-
координаттық осьтердің бірлік векторлары
деп аталады.
1,
2,
3
векторлары-
координаттық осьтердің бірлік векторлары
деп аталады.
АКЖ-де 1, 2, 3 ұзындықтары бірдей болуға міндетті емес,,,,,,
12. Кеңістіктегі акж (декарттық тікбұрышты координаттар жүйесі )(рис. 4.4) (Афиндик)

О –координата
басы, Ох –абсцисса
осі, Оy –
ордината
осі, Оz –
аппликата
осі,![]() -
базистік
векторлар. Oxy, Oxz, Oyz –
координаттық
жазықтықтар,
-
базистік
векторлар. Oxy, Oxz, Oyz –
координаттық
жазықтықтар, ![]() -М
нүктесінің
абсциссасы(
-М
нүктесінің
абсциссасы(![]() - M нүктесінің
Ох осіне
түсірілген
Оyz
осіне параллель проекциясы),
- M нүктесінің
Ох осіне
түсірілген
Оyz
осіне параллель проекциясы), ![]() -
M
нүктесінің ординатасы (
-
M
нүктесінің ординатасы (![]() - M
нүктесінің Oy
осіне түсірілген
Oxz
осіне параллель проекциясы),
- M
нүктесінің Oy
осіне түсірілген
Oxz
осіне параллель проекциясы), ![]() -
M
нүктесінің апликатасы (
-
M
нүктесінің апликатасы (![]() -M нүктесінің
Oz осіне
түсірілген
Oxy
осіне параллель проекциясы).
-M нүктесінің
Oz осіне
түсірілген
Oxy
осіне параллель проекциясы).

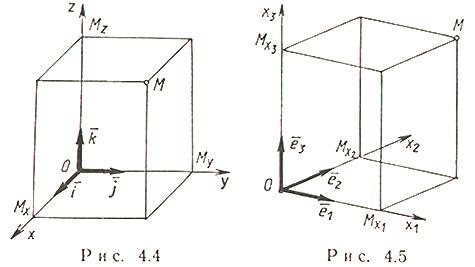
Сонымен
кеңістіктегі ДКЖ деп өзара перпендикуляр
болатын О(.)-де
қиылысатын және
 1|=
2|=
3|-ретелген
үш координаттық осьтердің топтастыруын
айтамыз.
1|=
2|=
3|-ретелген
үш координаттық осьтердің топтастыруын
айтамыз.
1=
2=
3=
13.Кесіндіні берілген қатынаста бөлу. AB кесіндісін жəне M
нүктесін қарастырамыз, онда

M
нүктесінің координаталарын табалық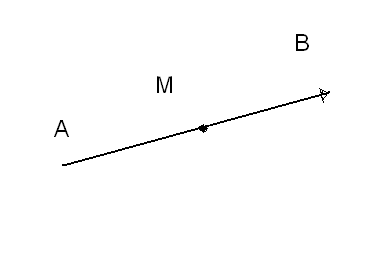
A( ,
,
 ,
,
 )
, B(
)
, B( ,
,
 ,
,
 ), M
(x,
y,
z)
болсын. Онда
), M
(x,
y,
z)
болсын. Онда
 =
( x
−
)(y
–
)(
z
–
),
=
( x
−
)(y
–
)(
z
–
), = (
–
x,
–
y,
−
z)
. AM||
MB,
= (
–
x,
–
y,
−
z)
. AM||
MB,
онда AM = λ ⋅ MB . Немесе
x − = λ ( − x)⇒(1 + λ)x = + λ ⇒
x=
Дəл солай,
y= ,z=
,z= .
.
14. Екі вектордың скаляр көбейтіндісі деп сол векторлардың ұзындықтары мен екеуінің арасындағы бұрышының косинусының көбейтіндісін айтады:
а ![]() b =
|а|
|b|
cosa^
b.
b =
|а|
|b|
cosa^
b.
Анықтама бойынша скаляр көбейтінді скаляр шама болады.
Оның төмендегідей қасиеттері бар:
1) ab=ba
2) Егер a![]() b болса,
онда а
b= 0.
b болса,
онда а
b= 0.
3) Егер а= b болса, онда ab=а2=|а|2, яғни а2=|а|2.
Осыдан:
|а|=|![]() |.
|.
4) а
![]() b =
( ab).
b =
( ab).
5) (a+b) с=ac+ bc.
6) Cos ab= ![]() .
.
Скаляр көбейтіндінің геометриялық мағынасы да бар. Егер а мен
b-нің
арасындағы бұрыш ![]() -ге
тең болса, онда
анықтама
бойынша а
b =
|а|
|b|
cos
=|а|
праb= |b|
прba,
-ге
тең болса, онда
анықтама
бойынша а
b =
|а|
|b|
cos
=|а|
праb= |b|
прba,
себебі
|а|cos = прba, |b|cos = праb.
Осыдан
прba=![]() ,
праb=
,
праb=![]() ,
,
яғни бір вектордың екінші векторға түскен проекциясы екеуінің скаляр көбейтіндісі мен бірінің модулы арқылы өрнектеледі. Егер көбейткіш векторлардың координаталары берілсе: a{X1; Y1; Z1}, b{X2; Y2; Z2}, онда
а b =X1X2 + Y1Y2 + Z1Z2.
Осыдан 3) қасиет бойынша кез келген a{ X; Y; Z } векторының ұзындығы оның координаталары арқылы төмендегі түрде өрнектеледі:
|а|=![]() .
.
Ал 2) шарт бойынша екі вектордың перпендикулярлық шарты
X1X2 + Y1Y2 + Z1Z2 =0
түрінде жазылады. Кез келген вектордың координаталар осьтерімен жасайтын бұрыштарының косинустарын бағыттаушы косинустар дейді. Оларды да, скаляр көбейтіндіні пайдаланып, вектордың координаталары арқылы өрнектеуге болады. Егер a{ X; Y; Z } векторы берілсе, онда
a
i=|а|cos(a^
i)
= |а|cos![]() =X,
=X,
яғни
|а|cos =X, ал |а|= , осыдан
cos
= ![]()
Сол сияқты,
cos![]() =
=![]() ,
,
cos
=![]() ,
,
мұнда , , - берілген а векторының сәйкес абсциссалар, ординаталар, апликаталар осьтерімен жасайтын бұрыштары.
17.Оң үштіктің және сол үштіктің анықтамасы.Векторлардың векторлық көбейтіндісінің анықтамасы және оның геометриялық мағынасы.
 векторы
берілсін.Егер 3коллинеар емес
векторлары оң(сол) қолдың бас бармақ,сұқ
қол, ортан қол саусақтарына сәйкес
орналасса онда
векторын
үштігін оң,сол үштігі д.а.
векторы
берілсін.Егер 3коллинеар емес
векторлары оң(сол) қолдың бас бармақ,сұқ
қол, ортан қол саусақтарына сәйкес
орналасса онда
векторын
үштігін оң,сол үштігі д.а.
Бағыты
сағат тіліне қарама қарсы геометриялық
оң бағыт,сол бағыт сағат тілімен
бағыттас.Кез келген үш векторынан алты
үштік вектор құрауға болады.(
),( ,(
,( кез
келген үштікте екі вектордың орнын
ауыстырсақ үштік атын өзгертеді.Егер
координата жүйе базистік вектор оң
үштік құраса координаталық жүйе оң д.а.
кез
келген үштікте екі вектордың орнын
ауыстырсақ үштік атын өзгертеді.Егер
координата жүйе базистік вектор оң
үштік құраса координаталық жүйе оң д.а.
Егер координата жүйе базистік вектор сол үштік құраса координаталық жүйе сол д.а. Көбіне оң үштікті қолданамыз
Анықтама:О
дік емес
 векторының векторлық көбейтіндісі деп
келесі үш шартты қанағаттандыратын
векторының векторлық көбейтіндісі деп
келесі үш шартты қанағаттандыратын
 векторын
айтамыз және келесі түрде белгіленеді.
векторын
айтамыз және келесі түрде белгіленеді.
 1)
–оң үштік
1)
–оң үштік
 ,
,

Теорема:
 вектордың
көбейтіндісі нөлдік емес,
векторлық көбейтіндісі нөлге тең
болады,сонда және сонда ғана коллинеар
болса
вектордың
көбейтіндісі нөлдік емес,
векторлық көбейтіндісі нөлге тең
болады,сонда және сонда ғана коллинеар
болса
 ,
, ,
,

Дәлелдеу

 ,
,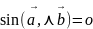
,
 немесе
немесе
Демек. коллинеар векторлар
коллинеар векторлар

Векторлық көбейтіндісі гоеметриялық мағынасы
Қасиеттері:
 =-
=-
2)
3)
4)
