4. Сызықты тәуелді векторлар жүйесінің анықтамасы. Коллениар және компланар векторлардың сызықтық тәуелділігін көрсету.
Анықтама: {а1 а2,,,, аn} векторлар жүйесі және α1, α2,,,,,, αn є R сандары берілген. α1 а1+
+α2 а2+,,,+αn аn- өрнекті а1 а2,,,, аn векторының сызықты комбиациясы деп аталады.
α1, α2,,,,,, αn- сызықты комбинацияның коэфиценттері деп аталады.
Анықтама: В- векторын а1 а2,,,, аn векторы арқылы сызықты өрнектеледі деп атайды, егер табылады α1, α2,,,,,, αn є R, В= α1 а1++α2 а2+,,,+αn аn.
Анықтама: Егер θ-к векторын а1 а2,,,, аn арқылы α1, α2,,,,,, αn коэффицентінің жоқ дегенде біреуі 0-ден өзгеше болатыдай етіп өрнектеуге мүмкін болса, онда {а1 а2,,,, аn} векторлар жүйесі сызықты тәуелді деп аталады.
Теорема: (коллениар болу белгісі) Екі вектор коллениар болады сонда және тек сонда ғана егер табылады жалғыз α саны 1 вектор 2-ші вектор арқылы сызықты өрнектеледі.
Дәлелдеу: (→) а векторы коллениар в векторына болғандықтан олар параллель немесе бір түзудің бойында жатады. а және в векторын бір нүктеге көшірейік.
Векторлады санға көбейту амалының анықтамасы бойынша табылады α: а= αβ.
Табылады α1 ≠ α2 және а= α1в
-
а= α2в
θ= (α1- α2)в → α1= α2 бұл қарама қайшылық.
(←) табылады α : а= α в. Векторды санға көбейту амалының анықтамасы бойынша а коллениар в векторына.
Теораема: ( компланар болу шарты) Үш верктор компланар болады сонда және тек сонда ғана егер олардың ішінде біреуі қалған екеуі арқылы сызықты өрнектелсе.
а, в, с компланар ↔ табылады α, β є R: с= αа +βв.
Дәлелдеуі: (→) а,в,с компланар. а,в, с верторларын бір нүктеге көшіреміз. а, в векторларын сәйкес α, β нақты сандарына көбейтеміз: αа, βв векторлардан құралған паралелограмның с векторы диагоналі болып табылу керек.
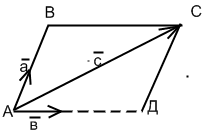с
векторының ұшы арқылы а
векторына параллель түзу және в
векторына параллель түзу жүргіземіз.
а
және в
векторын сол түзуге дейін созамыз. с=
АС+АД.
а
коллениар АВ} компланар болу белгісі
АВ=
αа
в коллениар АД} АД= βв → с= αа +βв.
5. Сызықты тәуелді векторлар жүйесінің қасиеттерін дәлелдеу.
Сызықты тәуелділіктің алгебралық қасиеттері
1. Егер векторлар жүйесінде θ вектор бар болса, онда ол жүйе сыықты тәуелді болады.
Дәлелдеу:
{а1
а2,,,,
аn}
і:
а=θ
1≤ і ≤ n α1
а1+α2
а2+,,+αі-1
аі-1+αі
аі+
αі+1
аі+1,,,
+ α
nаn=
θ
α1= α2=...= αі-1=0, αі=1, αі+1=...= α n=0, 0* а1+0* а2+....+0* аі-1+ 1 аі+...+0*аn=θ.
2. Бір вектордан тұратын жүйе сызықты тәуелді болады сонда және тек сонда ғана егер бұл вектор θ болса {а}- сызықты тәуелді ↔ а=θ.
Дәлелдеу: (→){а}- сызықты тәуелді α*а=θ α≠0, а=θ.
(←)а=θ α*а=θ α≠0 α=1 ↔ {а}- сызықты тәуелді.
3. Егер сызықты тәуелді векторлар жүйесіне бірнеші вектор біріктірсек, онда жаңа жүйеде сызықты тәуелді болады.
Дәлелдеу: (*) {а1 а2,,,, аn}- сызықты тәуелді жүйе.
(**){а1 а2,,аn, аn +1,,, аn+к}- сызықты тәуелді. (*)-сызықты тәуелді болғандықтан α1 а1+α2 а2+,,,+αn аn=θ- те кем дегенде 1 коэффиценті 0-ден өзгеше. Анықтық үшін αn=1, келесі теңдікті құрайық α1 а1+α2 а2+,,,+1* аn+ αі+1 аі+1+,,+αn+k an+k=θ бұл теңдікте 1 коэффицент 0- ден өзгеше, демек (**)- сызықты тәуелді.
4. Векторлар жүйесі сызықты тәуелді болу үшін жүйенің ішіндегі жоқ дегенде 1 вектор қалғандары арқылы сызықты өрнектелуі қажетті және жеткілікті.
Дәлелдеу: (→){а1 а2,,,, аn}- сызықты тәуелді. α1 а1+α2 а2+,,,+αn аn=θ- комбинацияда жоқ дегенде 1 коэффицент 0-ден өзгеше, анықтық үшін αn≠0 онда (*) келесі түрде жазамыз.
аn= (-α1/ αn) а1+,,,+ (-αn-1/ αn) аn-1.
(←) {а1 а2,,,, аn} жүйеде а1 векторы қалғандары арқылы сызықты өрнектелсін
a1= β2 a2+ β3 a3+,,,+ βn an , 1* a1- β2 a2-,,,- βn an=θ демек {а1 а2,,,, аn}- сызықты тәуелді.
Сызықты тәуелділіктің геометриялық қасиеттері
1. 2 вектордан құралған жүйе сызықты тәуелді болады сонда және тек сонда ғана егер олар коллениар болса. Дәлелдеу: α1 ≠0 α а = - βв а= -(β/2)в коллениар болу белгісі бойынша а,в векторлары коллениар болады. (←) а,в коллениар болады егер а=α в.
2. (→) а, в, с- сызықты тәуелді α а +β в+ γ с= θ α ≠0 а= -(β/2)в+ (-γ/2)с =0
(←) а, в, с компланар → табылады α, β с= α а+ βв → 1*с- α а- βв=θ.
3. Кеңістікте кез келген 4 вектор сызықты тәуелді жүйе құрайды.