
- •1. Вектордың анықтамасы. Тең векторлардың анықтамасы.
- •2. Векторларды қосу амалының анықтамасы. Векторларды қосу амалының қасиеттерін дәлелдеу.
- •3. Векторды санға көбейту амалының анықтамасы. Векторды санға көбейту амалының қасиеттерін дәлелдеу.
- •4. Сызықты тәуелді векторлар жүйесінің анықтамасы. Коллениар және компланар векторлардың сызықтық тәуелділігін көрсету.
- •5. Сызықты тәуелді векторлар жүйесінің қасиеттерін дәлелдеу.
- •6. Сызықтық тәуелсіз векторлар жүйесінің анықтамасы. Мысалдар. Сызықтық тәуелсіз векторлар жүйесінің қасиеттері.
- •11.Кеңістіктегі акж
- •12. Кеңістіктегі акж (декарттық тікбұрышты координаттар жүйесі )(рис. 4.4) (Афиндик)
- •19.Векторлардың аралас көбейтіндісінің анықтамасы және геометриялық мағынасы.
- •20. Векторлардың аралас көбейтіндісінің қасиеттері мен есептеу формулалары:
- •21. Жазықтықтағы түзудің параметрлік,канондық,екі нүкте арқылы өтетін түзудің, кесінділермен берілген түзудің теңдеулерін қорытып шығару
- •28.Жазықтықтың параметрлік және үш нүкте арқылы өтетін теңдеуін қорытып шығару.
- •29.Жазықтықтың жалпы теңдеуін қорытып шығару.
- •30. Екі жазықтықтың өзара орналасуы туралы теореманы дәлелдеу.
- •34. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың есептеу формуласын қорытып шығару.
- •35. Кеңістіктегі екі түзудің өзара орналасуы.
- •36. Кеңістіктегі түзу мен жазықтықтың өзара орналасуы.
- •37. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыштың синусын есептеу формуласын қорытып шығару.
- •38. Кеңістікте нүктеден түзуге дейінгі арақашықтықтың есептеу формуласын қорытып шығару.
- •46, Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
- •47,Эллипс (канондық теңдеуін қорыту, фокалдық радиустарды есептеу, эксцентриситет, параметрлік теңдеу).
- •47,Эллипс
- •48,Гипербола
- •46,Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
- •1 Сурет 1
- •1 Сурет 2
- •52. Екінші ретті сызықтардың типтерге бөлініуі
- •53. Екінші ретті сызықтардың жалпы теңдеуінің инварианттары туралы теорема.
- •Екінші ретті сызықтардың центрі туралы теоремаларды дәлелдеу. Центрі бар және центрі жоқ қисықтар.
- •2. Гиперболалық параболоидтың канондық теңдеуі. Гиперболалық параболоидтың қималары.
- •64. Целиндтлік бет және оның қималары
- •65. Эллипстік параболоидтың канондық теңдеуін қорытып шығару. Эллипстік параболоидтың қималары.
- •67. Гиперболалық параболоидтың түзу сызықты жасаушалары.
- •68. Екінші ретті беттердің жалпы теңдеуі. Екінші ретті беттердің типтерге бөлінуі.
- •69. Екінші ретті беттердің жалпы теңдеуін 17 канондық теңдеуге келтіру.
- •70. Екінші ретті беттердің жалпы теңдеуінің инварианттары
52. Екінші ретті сызықтардың типтерге бөлініуі
Егер F( x,y)=αx+βy+γ өрнегінің α мен β кем дегенде біреуі нөлден өзге болса, онда осы өрнеті дәрәжесі бірге тең айнымалылары х,у болатын көпмүше дейміз. 23.1-теоремасы (Жазықтықтағы кез келген түзу екі айнымалылы, дәрежесі бірге тең алгебралық теңдеу арқылы анықталады. Керісінше, екі айнымалылы кез келген дәрежесі бірге тең алгебралық теңдеудің шешімдер жиыны жазықтықтағы түзумен сипатталады.) бойынша, F( x,y)=0 теңдеуінің шешімдер жиыны жазықтықта орналасқан түзумен сипатталады.
Егер G( x,y)=α1х2+α2ху+ α3y2+ β1x+ β2y+γ өрнегінің α1, α2, α3 кем дегенде біреуі нөлге тең емес болса, онда G-ны дәрежесі екіге тең, айнымалылары х,у болатын көпмүше, ал ( x,y) координаталары G(x,y)=0 теңдеуін қанағаттандыратын жазықтықтағы нүктелер жиынын 2-ретті алгебралық сызық деп атайды. Алгебралық сызықтардың 9 түрі бар. Ішінде парабола, эллипс және гипербола секілділер.
Парабола
Бір ОХУ тікбұрышты Декарт координаталар жүйесінде
К1: у2=2рх, р>0, (1),
Теңдеуімен анықталған 2-ретті алгебралық сызық парабола деп аталады. (1) теңдеу параболаның канондық теңдеуі деп аталады. ОХ түзуі параболаның симметрия өсі болады, өйткені:
 β2=2рα
(-β)2=2рα
β2=2рα
(-β)2=2рα
яғни М1(α,β)ͼ К1 М2(α,-β)ͼ К1
ал М1 мен М2 нүктелер ОХ осіне қарағанда симметриалы болады. Параболаның бір симметрия өсі бар, ол ОХ өсі болады да параболаның өсі деп аталады. ОХ, ОУ остері-параболаның канондық остері, р коэффиценті- фокальді параметрі, F(p̸2;0) нүктесі- фокусы, ал х=-(р/2) түзуі- параболаның директрисасы деп аталады.
Эллипс
Бір ОХУ тікбұрышты Декарт координаталар жүйесінде
К2: х2/а2 + у2/b2 =1 a ≥b≥0, (2)
Теңдеуімен анықталған 2-ретті алгебралық сызық эллипс деп аталады. (2) теңдеу эллипстың канондық теңдеуі деп аталады. а=b тең болған жағдайда К3: х2+у2=а2 теңдеуіне түрленеді. Демек шеңбер эллипстің дербес жағдайы болып табылады. Эллипс мүшелері
 —
үлкен
жарты осі;
—
үлкен
жарты осі;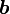 —
кіші
жарты осі;
—
кіші
жарты осі;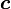 —
фокальдық
радиус (фокустары арасындағы жартылай
қашықтық);
—
фокальдық
радиус (фокустары арасындағы жартылай
қашықтық);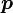 —
фокальдық
параметрі;
—
фокальдық
параметрі; —
перифокустық
қашықтық (эллипстегі нүктеден фокусқа
дейінгі ең жақын қашықтық);
—
перифокустық
қашықтық (эллипстегі нүктеден фокусқа
дейінгі ең жақын қашықтық);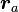 —
апофокустық
қашықтық (эллипстегі нүктеден фокусқа
дейінгі ең ұзын қашықтық);
—
апофокустық
қашықтық (эллипстегі нүктеден фокусқа
дейінгі ең ұзын қашықтық);
![]()
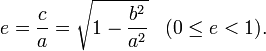
![]()
.
Гипербола
Бір ОХУ тікбұрышты Декарт координаталар жүйесінде
К3: х2/а2 - у2/b2 =1 a>0, b>0, (3)
Теңдеуімен анықталған 2-ретті алгебралық сызық гипербола деп аталады. (3) теңдеу гиперболаның канондық теңдеуі деп аталады. a=b дербес жағдайда К3 гиперболасы тең бүйірлі гипербола деп аталады.
Егер ОХУ координаталар жүйесін полюс айналасында -π/4 бұрышқа бұрсақ, онда бұрылған OUV жүйесінің өстері
 OU:
х+ у=0
, OV:х-у=0
теңдеулерімен анықталады. Ендеше,
М(х,у) нүктесінің жаңа координаталары
OU:
х+ у=0
, OV:х-у=0
теңдеулерімен анықталады. Ендеше,
М(х,у) нүктесінің жаңа координаталары
u=δ(M,OV)=(x-y)/ түбір астындағы 2 u=δ(M,OU)=(x+y)/ түбір астындағы 2
формулалар арқылы табылып, х2/а2 - у2/a2 =(x-y)(x+y) /a2 =2uv/a2 болады. Демек, OUV тікбұрышты Декарт координаталар жүйесінде теңбүйірлі гиперболаның теңдеуі:
К4: uv=a2/2
саны— гиперболаның нақты жарты осі;
саны— гиперболаның жорамал жарты осі;
=түбір астында(a2+b2)- cызықтық эксцентриситеті;
e=c/a= түбір астындағы(1+b2/a2) саны- гиперболаның сандық эксцентритеті;
(-а,0),(а,0)- гипербола төбелері;
F1(c,0), F2(-c,0)-гиперболаның оң және сол фокустары;
D1: x=a/e, D2: x=-a/e түзулері-гиперболаның оң және сол директрисалары;
А1: x/a+y/b=0 ,A2: x/a-y/b=0 түзулері – гиперболаның асимптоталары.
