
- •1. Вектордың анықтамасы. Тең векторлардың анықтамасы.
- •2. Векторларды қосу амалының анықтамасы. Векторларды қосу амалының қасиеттерін дәлелдеу.
- •3. Векторды санға көбейту амалының анықтамасы. Векторды санға көбейту амалының қасиеттерін дәлелдеу.
- •4. Сызықты тәуелді векторлар жүйесінің анықтамасы. Коллениар және компланар векторлардың сызықтық тәуелділігін көрсету.
- •5. Сызықты тәуелді векторлар жүйесінің қасиеттерін дәлелдеу.
- •6. Сызықтық тәуелсіз векторлар жүйесінің анықтамасы. Мысалдар. Сызықтық тәуелсіз векторлар жүйесінің қасиеттері.
- •11.Кеңістіктегі акж
- •12. Кеңістіктегі акж (декарттық тікбұрышты координаттар жүйесі )(рис. 4.4) (Афиндик)
- •19.Векторлардың аралас көбейтіндісінің анықтамасы және геометриялық мағынасы.
- •20. Векторлардың аралас көбейтіндісінің қасиеттері мен есептеу формулалары:
- •21. Жазықтықтағы түзудің параметрлік,канондық,екі нүкте арқылы өтетін түзудің, кесінділермен берілген түзудің теңдеулерін қорытып шығару
- •28.Жазықтықтың параметрлік және үш нүкте арқылы өтетін теңдеуін қорытып шығару.
- •29.Жазықтықтың жалпы теңдеуін қорытып шығару.
- •30. Екі жазықтықтың өзара орналасуы туралы теореманы дәлелдеу.
- •34. Кеңістіктегі нүктеден жазықтыққа дейінгі арақашықтықтың есептеу формуласын қорытып шығару.
- •35. Кеңістіктегі екі түзудің өзара орналасуы.
- •36. Кеңістіктегі түзу мен жазықтықтың өзара орналасуы.
- •37. Кеңістіктегі түзумен жазықтықтың арасындағы бұрыштың синусын есептеу формуласын қорытып шығару.
- •38. Кеңістікте нүктеден түзуге дейінгі арақашықтықтың есептеу формуласын қорытып шығару.
- •46, Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
- •47,Эллипс (канондық теңдеуін қорыту, фокалдық радиустарды есептеу, эксцентриситет, параметрлік теңдеу).
- •47,Эллипс
- •48,Гипербола
- •46,Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
- •1 Сурет 1
- •1 Сурет 2
- •52. Екінші ретті сызықтардың типтерге бөлініуі
- •53. Екінші ретті сызықтардың жалпы теңдеуінің инварианттары туралы теорема.
- •Екінші ретті сызықтардың центрі туралы теоремаларды дәлелдеу. Центрі бар және центрі жоқ қисықтар.
- •2. Гиперболалық параболоидтың канондық теңдеуі. Гиперболалық параболоидтың қималары.
- •64. Целиндтлік бет және оның қималары
- •65. Эллипстік параболоидтың канондық теңдеуін қорытып шығару. Эллипстік параболоидтың қималары.
- •67. Гиперболалық параболоидтың түзу сызықты жасаушалары.
- •68. Екінші ретті беттердің жалпы теңдеуі. Екінші ретті беттердің типтерге бөлінуі.
- •69. Екінші ретті беттердің жалпы теңдеуін 17 канондық теңдеуге келтіру.
- •70. Екінші ретті беттердің жалпы теңдеуінің инварианттары
46,Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.
В(і,j) i=c11e+c12j
B`(і,j) j=c21e+c22j
α<900
(i i)=c11(i i)+c12(i j)
(i j)=c11(i j)+c12(j j)
cosα=c11 │i││j│cos(∏/2-α)=c12 sinα=c12
(j i) =c21(i i)+c22(j i)
(j j)=c21(i j)+c22 (j j)
cos(∏/2+α)=c21 c22=cosα
c=│cosα sinα│
│-sinα cosα │
c= cos 2α+sin2α=1>0
a=B↑↑B`
R=(0,i,j) R`=(0,I,j)
x=x0+cosαx`-sinαy`
y=y0+sinαx`+cosαy`

1 Сурет 1
4
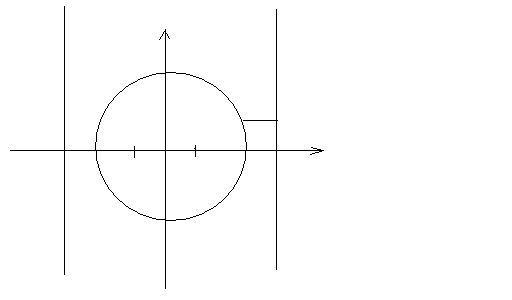 9.Эллипстің
және гиперболаның директрисаларының
қасиеттерін дәлелдеу 1)Эллипс
9.Эллипстің
және гиперболаның директрисаларының
қасиеттерін дәлелдеу 1)Эллипс
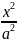 +
+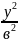 =1
х=
=1
х=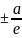 е
е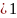 (1 сурет
1)
(1 сурет
1)
2
) Гипербола
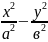 =1
х=
е
(
1 сурет 2)
=1
х=
е
(
1 сурет 2)
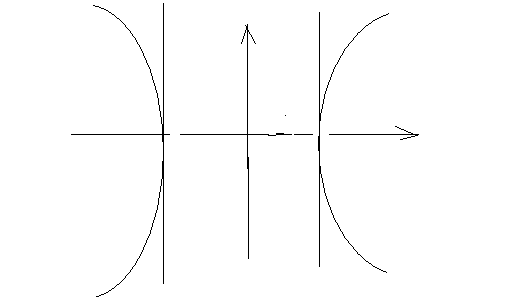
1 Сурет 2
Th 1.Эллипстің (гиперболаның) кез келген нүктесінен сәйкес фокусына дейінгі арақашықтығының сол нүктемен сәйкес келетін директрисасына дейінгі арақашықтығына дейінгі қатынасы эллипстің (гиперболаның) экстреситетіне тең болады.
Д.у
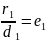
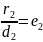
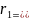 a −
a −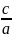 x
x
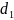 =
=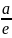 -x
-x
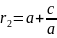 x
x
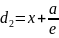
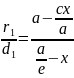 =
=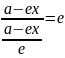
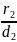 =
=
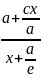 =
=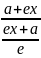 = e
= e
Th 2
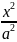 +
+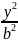 =1
−
=1 берілсін.Егер
жазықтықтағы қандай да бір нүктеден
эллипс
(гиперболаның)
сәйкес фокусына дейінгі арақашықтығына
дейінгі арақатынасы эллипс (гипербола)
экстреситетіне тең.тең болса,онда ол
нүкте эллипсқа тең болады.
=1
−
=1 берілсін.Егер
жазықтықтағы қандай да бір нүктеден
эллипс
(гиперболаның)
сәйкес фокусына дейінгі арақашықтығына
дейінгі арақатынасы эллипс (гипербола)
экстреситетіне тең.тең болса,онда ол
нүкте эллипсқа тең болады.
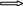 Д.у
Д.у
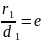
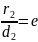
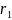 =
=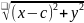
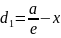 у
у
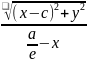 =e
=e
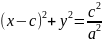
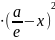
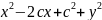 =
=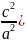 -2
-2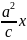 +
+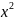 )
-2cx+
)
-2cx+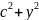 =
=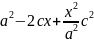
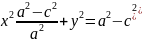 1)a
1)a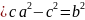 2)a
2)a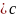
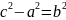
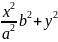 =
=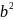 +
=1
(эллипс)
+
=1
(эллипс)
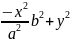 =
=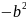
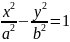 (гипербола)
(гипербола)
50.Параболаның параметрлік теңдеуін қорыту
(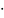 )
F, ДД`- түзу
)
F, ДД`- түзу
(
)
F тиісті
емес ДД`
тиісті
емес ДД`
Анықтама.Ғ нүктесіне дейінгі және ДД`түзуіне дейінгі арақашықтықтары тең болатын жазықтықтағы нүктелер жиынын парабола д.а.
D
(F, ДД`)=P ДД`: x= -
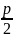 FM=
FM=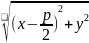
d(M,
ДД`)=
+ x 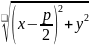 =
=
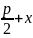
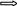 -px+
-px+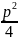 +
+
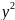 =
+px
+
=
+px
+
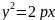
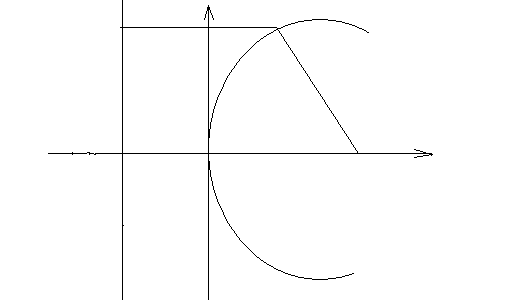 (1)
параболаның параметрлік теңдеуі
(1)
параболаның параметрлік теңдеуі
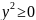 p
p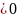 x
x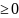
1->
y=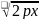 ,
x+
,
x+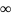 y+
y+
y=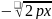 x+
y-
x+
y-
(1)
теңдеуде
у дәрежесі жұп болғандықтан ох осі
симметриялы параболаға О(0,0)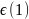
51.Екінші ретті сызықтардың жалпы теңдеуі. Екінші ретті сызықтардың үш түрге бөлінуі.
(1)
F(x,y) =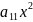 +2
+2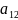 xy+
xy+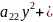 2
2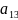 x+2
x+2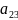 y+
y+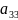
F(x,y) =0 +2 xy+ 2 x+2 y+ =0 жалпы теңдеу
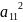 +
+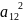 +
+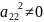
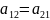 =
=
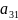
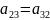
1)ТКЖ
α
бұрышына
бұрамыз.
x=x`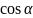 -y`
-y`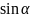
y=x`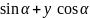
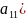 +2
(x`
-y`
)+x`
)+
+2
(x`
-y`
)+x`
)+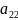 (
(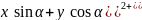 2
(x`
-y`
2
(x`
-y`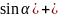 2
2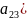 x`
x`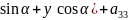 =0
=0
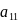 =
=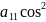 α+2
α+2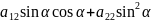
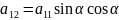 +
+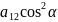 –
–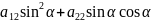
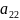 =
=
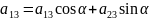
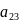 =
=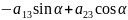
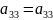 Ықшамдау
үшін
Ықшамдау
үшін
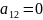 α іздейміз.
α іздейміз.
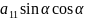 +
+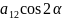 +
+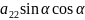 =0
=0
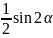 (
(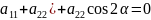
(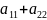 )=
-
)=
-
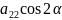
Ctg
2α= −
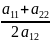 (1)->(2)
(1)->(2)
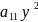 +
+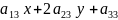 =0
=0
(2)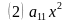 +
+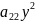 +2
+2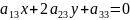
2) x=x`+ y=y`+ (2)` теңдеуге көшеміз
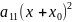 +
+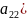 +2
+2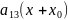 +2
+2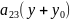 +
=0
+
=0
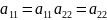
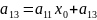
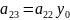 +
+
+
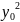 +2
+2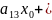 2
2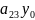 +
+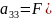 ,
,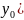
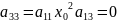
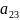 =0
=0
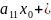
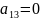
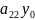 +
+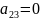
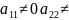 0
0
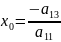 =
--
=
--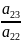
M(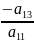 , --
, --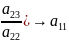 +
+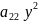 +
+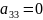
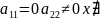 =
--
=
--
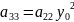 +2
+2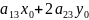 +
+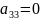
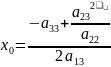
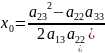
(2)`->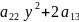 x`=0
x`=0
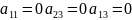
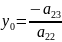 0
0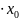 +0=0
-кез
келген сан
+0=0
-кез
келген сан
(2)`->
`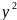 +
+
Теңдеу Екінші ретті сызықтардың жалпы теңдеуі. Жазықтықтағы бұрышқа бұру және координаталар басын көшіру түрлендірулері арқылы келесі 3 түрге келтіріледі.
+
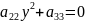
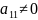
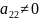
+2
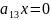
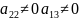
3)
