38. Кеңістікте нүктеден түзуге дейінгі арақашықтықтың есептеу формуласын қорытып шығару.

а: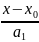 = =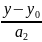 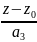түзуі мен осы түзуден тыс жатқан Т(x_1, y₁,z₁) нүктесі берілсін .

1. Т нүктесі арқылы а түзуіне перпендикуляр α жазықтығын жүргізейік. α жазықтығының а түзуімен қиылысу нүктесін табайық. Ол F нүктесі болсын. Т нүктесінен а түзуіне дейінгі арақашықтық ТF кесіндісінің ұзындығы ретіндее табылады.

2. а түзуінен Т нүктесіне дейінгі қашықтықты , а және ТМ векторлары бойынша жасалған параллелограмның биіктігі ретінде табуға болады. Мұндағы М – а түзуінің бастаапқы нүктесі, ал а векторы – осы түзудің бағыттаушы векторы

h=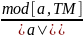

46, Жазықтықта тікбұрышты координаталар жүйесінде бір базистен екінші базиске көшу формулаларын қорытып шығару.

47,Эллипс (канондық теңдеуін қорыту, фокалдық радиустарды есептеу, эксцентриситет, параметрлік теңдеу).

48 Гипербола (канондық теңдеуін қорыту, фокалдық радиустарды есептеу, эксцентриситет, параметрлік теңдеу, асимптоталар).

47,Эллипс

Ғ1, Ғ2 – жазықтықта берілген [Ғ1Ғ2] =2С (арасындағы арақашықтық)

2а>2c( а санын қарастырамыз)

Анықтама: Ғ1, Ғ2 нүктелеріне дейінгі арақашықтықтарының қосындысы өзгермейтін сан болатын жазықтықтағы нүктелер жиынын эллипс деп атаймыз.

r1+ r2=2а

М(х,у)

r2 r1

Ғ2(-с,0) Ғ1(с,0)

r1+ r2=2а (1)

r1,r2-фокалдық радиустар

Ғ1, Ғ2-фокустары

r1=√(х-с)2+у2 r2=√(х+с)2+у2

1. => √(х-с)2+у2+ √(х+с)2+у2 =2а

√(х-с)2+у2=2а-√(х+с)2+у2

(х-с)2+у2=4а2-4а√(х+с)2+у2 + (х+с)2+у2

х2-2сх+с2+у2= 4а2-4а√(х+с)2+у2+х2+2сх+с2+у2

а√ (х+с)2+у2=сх+а2

а2(х+с)2+а2у2=с2х2+2а2сх+а4

а2х2+2а2сх+с2а2+а2у2=с2х2+2а2сх+а4

(а2-с2)х2+а2у2=а2( а2-с2)

а>с, а2-с2>0 => а2-с2=в2

в2х2+а2у2=а2в2 / а2в2

х2/а2+у2/в2=1 (2) эллипстің канондық теңдеуі

2. =>х2/а2≤1 , у2/в2≤1 => │х│≤а │у│≤в

(.)М(х ,у)∊ℰ(эллипс)=>М1(-х,у), М2(-х,-у), М3(х,-у) ∊ℰ=>ОХ ,ОУ - ℰ симметриялы осьтері

(.)О(0,0)- симметрия центрі

фокалдық радиустарды есептейік

r1=√(х-с)2+у2 =(2) √х2-2сх+с2+(1-х2/а2)в2=√ х2-2сх+с2+в2-в2х2/а2= √х2(1-в2/а2)-2сх+с2+в2= │а2-с2=в2,с2+в2=а2, а2-в2=с2│=√х2с2/а2-2сх+а2=√(а-сх/а)2=│а-сх/а│=[с<а,│х│≤а]=а-сх/а

r2=а+сх/а дәл алдыңғы секілді өрнектейміз

Анықтама: е=с/а саны эллипстің эксцентриситеті

Д.а. с<а=>е<1

с2==а2-в2 =>е=√а2-в2/а=√1-в2/а2 в-конст

е↑<=>эллипс созылады, а↑өседі

е↓<=>эллипс сығылады а↓ кішірейеді

келесі теңдеуді қарастырайық(3) {х=аcost, y=bsint (эллипстің параметрлік теңдеуі)

t∊[0,2∏] cost=x/a sint=y/b

sin2t+cos2t=1=> x2/a2+y2/b2=1

48,Гипербола

Ғ₁,Ғ₂ [Ғ₁Ғ₂] =2С 2а<2c

Анықтама: Ғ₁,Ғ₂ нүктелеріне дейінгі арақашықтықтарының айырмасының модулі, өзгермейтін сан болатын жазықтықтағы нүктелер жиынын гипербола деп атаймыз.

│r_1-r_2│=2а(1)

r₁=√(х-с)²+у² r₂=√(х+с)²+у² (1)=>│√(х-с)²+у² - √(х+с)²+у² │=2а

√(х-с)²+у² - √(х+с)²+у²=±2а

√(х-с)²+у² =±2а+√(х+с)²+у²

х²-2сх+с²+у²=4а²±4а√(х+с)²+у² +х²+2сх+с²+у²

±а√(х+с)²+у²=а²+сх

а²х²+2а²х+а²с²+а²у²=а⁴+2а²сх+с²х²

(с²-а²)х²-а²у²=а²(с²-а²)

с>а=> с²-а²=в², в²х²-а²у²=а²в²=>/ а²в²

х²/а²-у²/в²=1(2) гиперболаның канондық теңдеуі

1. =>у²=(х²/а²-1)в²=> х²/а²-1≥0 х²/а²≥1 │х│≥а у∊(-∞;∞)

r_1, r_2, r_1, r₂

оң оң сол сол

оң

r₁₌=√(х-с)²+у² =√(х-с)²+(х²/а²-1)в²=√х²-2сх+с²+в²х²/а²-в²=√х²(а²+в²)/а²-2сх+с²-в²=│с²-а²=в²│=√с²х²/а²-2сх+а²=√(с²х/а-а)²=│сх/а-а│=│х≥а, с/а>1│=сх/а-а

r_1, = а-сх/а _, r_2, = сх/а+а _, r₂= - сх/а-а

сол оң сол

е=с/а , с>а=>е>1 е=√а²+в²/а²=√1+в²/а²

а=конст. 1. в→0<=> е→1 бұл жағдайда гипербола бұтақтары ох қарай сығылады және фокустары төбелеріне қарай жақындайды.

2. в→∞ в↑<=> е↑ бұл жа бұл жағдайда гипербола бұтақтары кеңейеді және фокустары төбесінен алыстайды.

у=±в√х²/а²-1 , у>0, у=вх/а

lim(У-у)= lim(вх/а-в√х²-а²/а)=в/а lim(х-√х²-а²)=в/а lim(х-√х²-а²) (х+√х²-а²)/ (х+√х²-а²)=в/а lim(х²-х²+а²)/

х→∞ х→∞ х→∞ х→∞ х→∞

(х+√х²-а²)=0

у₁==вх/а у₂=-вх/а асимптота

сһt=е^t+е^-t/2 sht= е^t-е^-t/2 сһ²t - sh²t=1

х=а сһt, у=в sht параметрлік теңдеуі

х/а= сһt у/в= sht х²/а²-у²/в²=1

ескерту1: а=в х²/а²-у²/а²=1 х²-у²=а²(1)

ескерту2: х²/а²-у²/в²=1 -х²/а²+у²/в²=1(2)