Решение

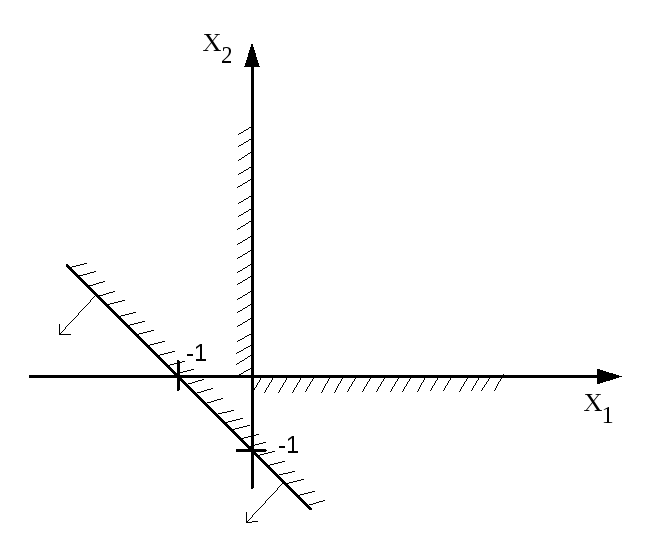
Построим область допустимых решений задачи. Из рис.7 видно, что нет точек одновременно удовлетворяющих всем ограничениям, т.е. область допустимых решений пуста. Таким образом задача не имеет решения.

(а)

Рис.7 Пример области допустимых решений ЗЛП.

Пример 3 Решить геометрическим способом ЗЛП

z=x₁+x₂  max

x₁-x₂  1 (a)

x₁  0, x₂  0

Решение

Построим область допустимых решений задачи. Из рис.8 видно, что эта область неограниченная. Целевая функция zна этой области допустимых решений не ограничена сверху, так при сдвиге вправо целевая функция возрастает, а сдвигать вправо модно до бесконечности. Следовательно, не существует точки, в которой функцияzдостигает максимума, т.е. задача не имеет решения.

Н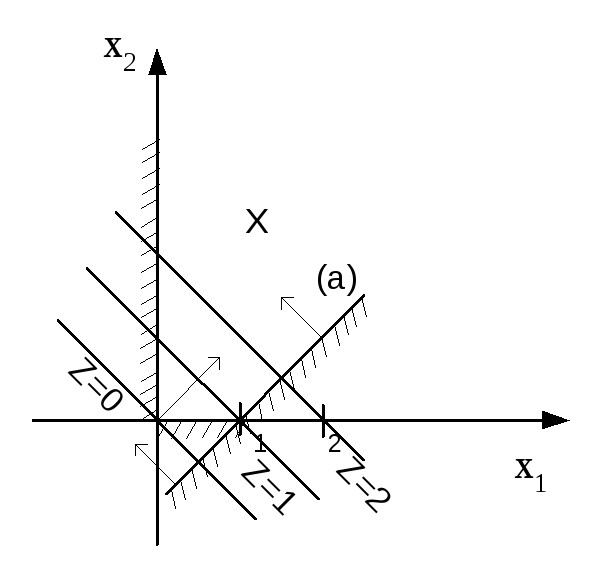еограниченность области допустимых решений в сочетании с неограниченностью целевой функции и приводит к тому, что задача не имеет решения. Неограниченность только области допустимых решений не является препятствием для существования решения. Так задача

z=x₁+x₂  min

x₁-x₂  1

x₁  0, x₂  0

Рис.8 Пример области допустимых решений ЗЛП имеет ту же область

допустимых решений, что и в примере 4 (рис.8). Однако целевая функция z задачи минимизации на той же области уже является ограниченной снизу (z0 для любых допустимых решений) и имеет минимум равный z=0 в точке x₁^*=0, x₂^*=0.

3. Геометрическая интерпретация ЗЛП в канонической форме.

Геометрическую интерпретацию ЗЛП в канонической форме рассмотрим в частном случае, когда число переменных n на два больше, чем число независимых уравнений m, которым они должны удовлетворять: n-m=2. Тогда две из n переменных, скажем x₁ и x₂, можно выбрать в качестве свободных, а остальные m сделать базисными и выразить из через свободные. Предположим, что это сделано. Получим m=n-2 уравнений вида:

x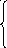₃ = ₃₁x₁ + ₃₂x₂ + ₃

x₄ = ₄₁x₁ + ₄₂x₂ + ₄ (4)



x_n = _n1x₁ + _n2x₂ + _n

Дадим ЗЛП геометрическую интерпретацию. Переменные x₁ , x₂ ,…, x_n должны удовлетворять условию неотрицательности, т.е.:

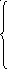x₃ = ₃₁x₁ + ₃₂x₂ + ₃  0

x₄ = ₄₁x₁ + ₄₂x₂ + ₄  0 (5)



x_n = _n1x₁ + _n2x₂ + _n  0

x₁ 0, x₂ 0

Построим область допустимых решений, удовлетворяющих указанным выше условиям.

Б

ОДР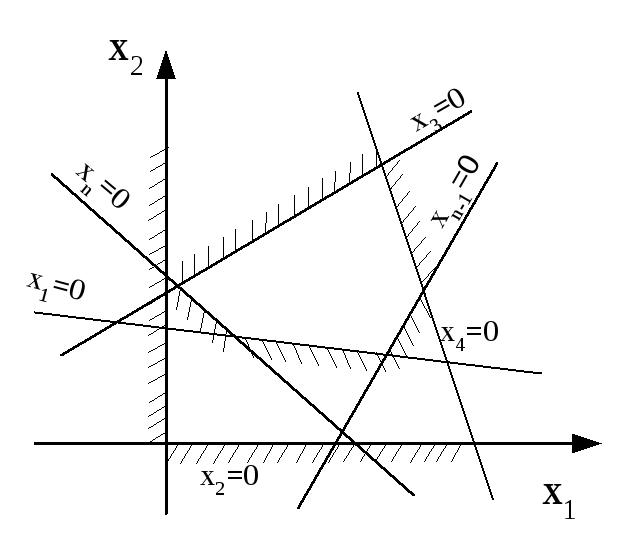

ез штриховки обозначена “допустимая сторона”, где соответствующая переменная больше нуля.

Если ОДР не пуста, то возникает вопрос о нахождении из числа допустимых оптимального решения, т.е. такого, которое обращает, например, в максимум целевую линейную функцию

z= c₁x₁ + c₂x₂+ …+ c_nx_n (6)

Рис.9 Область допустимых решений (ОДР)

Чтобы решить поставленную задачу, выразим целевую функцию через свободные переменные x₁ и x₂. Для этого подставим выражения для переменных x₃, x₄, …, x_n из (4) в целевую функцию (6) и после приведения подобных членов получим

z = ₀ + ₁x₁ + ₂x₂ (7)

где ₀ – свободный член, которого в первоначальном виде y функции z не было, но при переходе к переменным x₁, x₂ он мог появиться. Теперь, используя геометрическую интерпретацию ОДР и целевую функцию (7), выраженную через две переменные (x₁, x₂), мы можем геометрически найти решение задачи (x₁^*, x₂^*). Зная значение свободных переменных x₁^*, x₂^* можно найти, подставляя их в (4), и значения базисных переменных и значение целевой функции.

Пример

Используя геометрическую интерпретацию решить ЗЛП в канонической форме:

z = -16x₁ – x₂ + x₃ + 5x₄ + 5x₅  max

при ограничениях

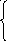2x₁ + x₂ + x₃ = 110

-2x₁ + 3x₂ + x₄ = 6

2x₁ + 4x₂ – x₅ = 8

x₁, x₂, x₃, x₄, x₅  0