
Практика по методам оптимизации
.docПрактические занятия №1,2 (4 час.)
Тема: Общая задача линейного программирования.
Рассматриваемые вопросы:
-
введение понятия общей задачи линейного программирования, стандартной и канонической ее формы;
-
рассмотрение вопроса построения математической модели для решения поставленной задачи;
-
приведение примеров прикладных задач линейного программирования.
-
Общая форма задачи линейного программирования .
В общем случае задача линейного программирования (ЗЛП) формулируется следующим образом: найти величины х1,…, хn , доставляющие минимум (максимум) линейной целевой функции
f![]() (x)
= c1x1
+ c2x2
+…+ cnxn
(x)
= c1x1
+ c2x2
+…+ cnxn
и удовлетворяющие ограничениям, которые могут быть только равенствами и неравенствами вида
a i1x1
+…+ainxn
bi ,
i = i,k ,
i1x1
+…+ainxn
bi ,
i = i,k ,
a i1x1
+…+ainxn
bi ,
i = i,k ,
i1x1
+…+ainxn
bi ,
i = i,k ,
a i1x1
+…+ainxn
bi ,
i = i,k .
i1x1
+…+ainxn
bi ,
i = i,k .
Cреди ограничений часто встречаются условия не отрицательности всех или части переменных
xj 0, j=1, 2, … ,S.
Хотя эти условия являются частным случаем представленных выше условий общего вида, на практике их обычно выделяют в особую группу.
В![]() более компактной записи общая задача
линейного программирования имеет вид:
более компактной записи общая задача
линейного программирования имеет вид:
п![]()
![]() ри
ограничениях
ри
ограничениях
г![]()
![]()
![]() де
aij,
bi, cj
– заданные постоянные величины.
де
aij,
bi, cj
– заданные постоянные величины.
2. Стандартная и каноническая формы задачи линейного программирования.
Различаются еще две основные формы задач линейного программирования в зависимости от наличия ограничений разного типа:
с![]() тандартная
форма ЗЛП
тандартная
форма ЗЛП
п![]()
![]() ри
ограничениях
ри
ограничениях
к![]()
![]() аноническая
форма ЗЛП
аноническая
форма ЗЛП
п![]() ри
ограничениях
ри
ограничениях
С![]()
![]() тандартная
форма ЗЛП интересна тем, что большое
число прикладных задач естественным
образом сводится к этому виду моделей.
тандартная
форма ЗЛП интересна тем, что большое
число прикладных задач естественным
образом сводится к этому виду моделей.
Каноническая форма ЗЛП важна ввиду того, что основные вычислительные методы решения ЗЛП разработаны именно для этой формы.
Указанные выше три формы ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть приведена к любой из двух остальных. Следовательно, любую ЗЛП можно привести к каноническому виду. Поэтому умение решать задачу в канонической форме позволяет решать задачу и в любой другой форме.
Некоторые из приемов, переводящих ЗЛП из одной формы в другую, перечислены ниже.
П![]() ереход
от задачи минимизации к задаче
максимизации. Для этого нужно изменить
знак критериальной функции, т.е. задача
ереход
от задачи минимизации к задаче
максимизации. Для этого нужно изменить
знак критериальной функции, т.е. задача
э![]() квивалентна
задача на поиск максимума
квивалентна
задача на поиск максимума
![]()
Переход к эквивалентной системе неравенств. Меняя знаки свободного члена и коэффициенты в ограничении – неравенства, можно поменять знак этого неравенства на обратный. Например, ограничения
ai1x1 +ai2x2+…+ainxn bi
можно заменить следующим:
(-ai1) x1 +(-ai2)+…+(-ain)xn (-bi)
Переход от ограничения - неравенства к равенству. Любое ограничение в форме неравенства введением дополнительной неотрицательной переменной может превратиться в ограничение – равенство. Так, к примеру, условие
ai1x1 +ai2x2+…+ainxn bi
эквивалентно двум ограничениям
ai1x1 +ai2x2+…+ainxn+xn+1= bi , xn+10.
Переменные типа xn+1 называют фиктивными или дополнительными.
Представление ограничения – равенства парой неравенств. Ограничение
ai1x1 +ai2x2+…+ainxn = bi
можно представить парой ограничений
ai1x1 +ai2x2+…+ainxn bi
(-ai1) x1 +(-ai2)+…+(-ain)xn (-bi)
Переход к неотрицательным переменным. Если на знак переменной xj не наложено ограничений, можно заменить ее разностью двух неотрицательных переменных
xj = x'j – x"j , x'j 0, x"j 0.
Переход от переменных, ограниченных снизу к неотрицательным переменным.
Пусть переменная ограничена снизу:
xj с
Заменив ее по формуле
xj = x'j +с
перейдем к задаче, в которой фигурирует неотрицательная переменная
x'j 0.
3.Примеры построения математических моделей линейного программирования.
Построение математической модели предполагает ответы на три вопроса.
1)Для определения каких переменных (неизвестных) необходимо построить модель?
2)В чём состоит цель решения задачи?
3)Какими ограничениями должны быть связаны переменные, чтобы выполнить условия, характерные для поставленной задачи?
Ответы на поставленные вопросы должны содержаться в словесном описании проблемы. Если эти ответы найдены, то цель задачи и ограничения представляются в виде математических функций переменных, значения которых требуется найти.
Рассмотрим несколько примеров построения математических моделей линейного программирования.
З

 адача
производственного планирования.
Некоторому заводу требуется определить
план производства и видов продукции.
Число видов ресурсов равно m.
При этом известно количество каждого
ресурса в: i=1,m.
Технологические возможности производства
определяются значениями чисел a
i j, i=1,m,
j=1,n,
показывающих, какое количество i-го
ресурса необходимо для выпуска одной
единицы j-го продукта.
Технология производства считается
линейной, т.е. предполагается, что все
затраты ресурсов растут прямо
пропорционально объёму выпуска.
адача
производственного планирования.
Некоторому заводу требуется определить
план производства и видов продукции.
Число видов ресурсов равно m.
При этом известно количество каждого
ресурса в: i=1,m.
Технологические возможности производства
определяются значениями чисел a
i j, i=1,m,
j=1,n,
показывающих, какое количество i-го
ресурса необходимо для выпуска одной
единицы j-го продукта.
Технология производства считается
линейной, т.е. предполагается, что все
затраты ресурсов растут прямо
пропорционально объёму выпуска.
З аданы
цены c j,
j=1,n, на
каждый вид продукта. Требуется определить
план производства, максимизирующий
стоимость выпущенной продукции.
аданы
цены c j,
j=1,n, на
каждый вид продукта. Требуется определить
план производства, максимизирующий
стоимость выпущенной продукции.
В описании задачи содержатся ответы на поставленные выше три вопроса.
План производства – вектор x={x1, x2, .. xn}, показывающий, какое количество каждого продукта будет произведено. Это – переменные задачи.
Ц![]() ель
решения задачи (или целевая функция) –
максимальная стоимость выпускаемой
продукции:
ель
решения задачи (или целевая функция) –
максимальная стоимость выпускаемой
продукции:
И![]() з
условия ограниченности ресурсов, с
одной стороны, и суммарных затрат
ресурсов для выполнения плана производства,
с другой стороны, строится система
ограничений математической модели:
з
условия ограниченности ресурсов, с
одной стороны, и суммарных затрат
ресурсов для выполнения плана производства,
с другой стороны, строится система
ограничений математической модели:
П![]() остроенная
математическая модель является ЗЛП в
стандартной форме.
остроенная
математическая модель является ЗЛП в
стандартной форме.
Задача о рационе. Предположим, что нужно выбрать суточный рацион питания, имея в распоряжении n продуктов, содержащих m питательных веществ.
Пусть v i j – количество i-го питательного вещества в единице j-го продукта, в i – суточная потребность организма в i-ом питательном веществе, с j – цена единицы j-го продукта. При этом требуется, чтобы цена суточного рациона питания была минимальной.
Суточный рацион питания – вектор x={x1, x2, ..xn}, где через xi обозначено суточное потребление i-го продукта.
Ц![]() ель
решения задачи – минимальная стоимость
суточного рациона питания:
ель
решения задачи – минимальная стоимость
суточного рациона питания:
И![]() з
условия полного удовлетворения
потребности организма в питательных
веществах строится система ограничений:
з
условия полного удовлетворения
потребности организма в питательных
веществах строится система ограничений:
П![]() отребление
j-го продукта должно быть,
разумеется, неотрицательно:
отребление
j-го продукта должно быть,
разумеется, неотрицательно:
Математическая модель представляет собой частный случай общей задачи линейного программирования (k=o, l=m, S=n).
Транспортная задача. Транспортная задача является одной из самых распространённых ЗЛП специального вида. Предположим, что имеется m складов, где хранится некоторый продукт в количествах a1, .., am, и n пункт в реализации этого продукта, потребности которых равны b1, .. bn. Требуется найти наиболее экономичный способ перевозки продукта со складов к потребителям, если затраты на перевозку единицы продукта с i-го склада в j-ый пункт потребления равны cij.
Пусть xij количество продукта, перевозимое с i-го склада в j-ый пункт потребления.
Т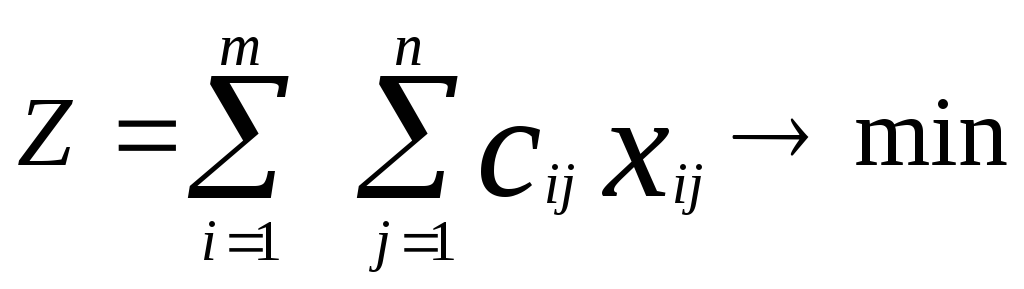 огда
целевая функция транспортных расходов,
которую требуется минимизировать,
выглядит так:
огда
целевая функция транспортных расходов,
которую требуется минимизировать,
выглядит так:
О![]()
![]() граничения
имеют вид
граничения
имеют вид
П![]() ервое
неравенство означает, что количество
продукта, вывезенного со склада, не
должно превышать запаса, второе – что
потребности каждого пункта должны быть
удовлетворены. Третье условие обеспечивает
неотрицательность планируемых объёмов
перевозок.
ервое
неравенство означает, что количество
продукта, вывезенного со склада, не
должно превышать запаса, второе – что
потребности каждого пункта должны быть
удовлетворены. Третье условие обеспечивает
неотрицательность планируемых объёмов
перевозок.
Особенностью полученной общей ЗЛП является двойная индексация переменных.
Задача о распределении ресурсов. Имеются какие-то ресурсы(сырьё, рабочая сила, оборудование):
R1, R2, .. Rm
в количествах соответственно
b1, b2, .. bm.
С помощью этих ресурсов могут производиться товары:
T1, T2, .. Tn
Для производства одной единицы товара Tj необходимо aij единиц ресурса Ri стоит dj руб. Каждая единица товара Tj может быть реализована по цене Cj.
По каждому виду товара количество произведённых единиц ограничевается спросом: известно, что рынок не может поглотить более, чем kj единиц товара Tj.
Обозначим план производства товаров через вектор x={x1, x2, .. xn}, где xj –планируемое количество товара Tj.
Т![]() огда
условия спроса налагают на них ограничения:
огда
условия спроса налагают на них ограничения:
Р![]() есурсов
должно хватить, отсюда возникают
ограничения:
есурсов
должно хватить, отсюда возникают
ограничения:
Выразим прибыль z в зависимости от переменных x1, .. xn
Себестоимость sj единицы товара Tj равна
Ч![]()
![]() истая
прибыль qj,
полученная от реализации одной единицы
товара Tj,
равна разнице между её продажной ценой
cj и
себестоимостью sj:
истая
прибыль qj,
полученная от реализации одной единицы
товара Tj,
равна разнице между её продажной ценой
cj и
себестоимостью sj:
По этой формуле получим чистые прибыли на единицу для всех товаров: q1, q2, .. qn.
О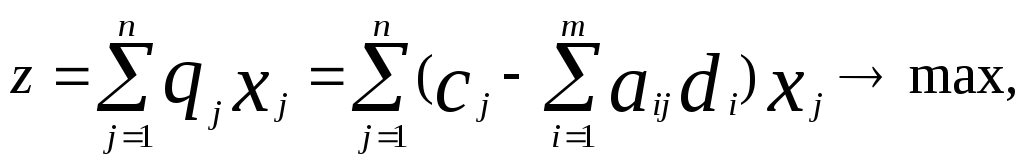 бщая
чистая прибыль от реализации всех
товаров будет
бщая
чистая прибыль от реализации всех
товаров будет
которую требуется максимизировать.
Задача о производстве сложного оборудования. Планируется производство сложного оборудования, каждый комплект которого состоит из n элементов: э1, э2, .. эn.
Заказы на производство этих элементов могут быть размещены на m разных предприятиях: П1, П2, .. Пm.
В
 течение заданного времени T
на предприятии П: можно изготовить aij
элементов типа Эj
(i=1,m ; j=1,n),
т. е. на каждом предприятии П: можно
изготовлять любые элементы Эj.
течение заданного времени T
на предприятии П: можно изготовить aij
элементов типа Эj
(i=1,m ; j=1,n),
т. е. на каждом предприятии П: можно
изготовлять любые элементы Эj.
Сдаче подлежат только полные комплекты оборудования, состоящие из набора всех элементов Э1, Э2, … Эn.
Требуется распределить заказы по предприятиям так, чтобы число полных комплектов оборудования, изготовленных за время T, было максимально.
Планируя производство оборудования, мы должны для каждого предприятия Пi указать, какую часть имеющегося в его распоряжении времени оно должно отдать на производство элементов Эj. Обозначим через xij долю времени T, которую предприятие Пj будет уделять производству элементов Эj(если этот элемент на данном предприятии не производится, то xij=0).
М![]() ы
должны соблюдать следующие ограничительные
условия: количество времени, которое
каждое предприятие затрачивает на
производство всех элементов, не должно
превышать общего запаса времени T
(а "доля" – единицы):
ы
должны соблюдать следующие ограничительные
условия: количество времени, которое
каждое предприятие затрачивает на
производство всех элементов, не должно
превышать общего запаса времени T
(а "доля" – единицы):
К![]() роме
того накладывается естественное условие
неотрицательности переменных:
роме
того накладывается естественное условие
неотрицательности переменных:
О![]() пределим
количество полных комплектов оборудования,
которое за время T поставят
все предприятия вместе.
пределим
количество полных комплектов оборудования,
которое за время T поставят
все предприятия вместе.
О![]() бщее
количество элементов Эj,
которое произведут все предприятия,
будет равно
бщее
количество элементов Эj,
которое произведут все предприятия,
будет равно
Т
 аким
образом при плане распределения заказов
xij
(i=1,m ; j=1,n)
будет произведено:
аким
образом при плане распределения заказов
xij
(i=1,m ; j=1,n)
будет произведено:
-N1 экземпляров элемента Э1,
-N2 экземпляров элемента Э2,
…..
-Nn экземпляров элемента Эn.
О![]() чевидно,
что полных комплектов оборудования, в
этом случае, будет произведено
чевидно,
что полных комплектов оборудования, в
этом случае, будет произведено
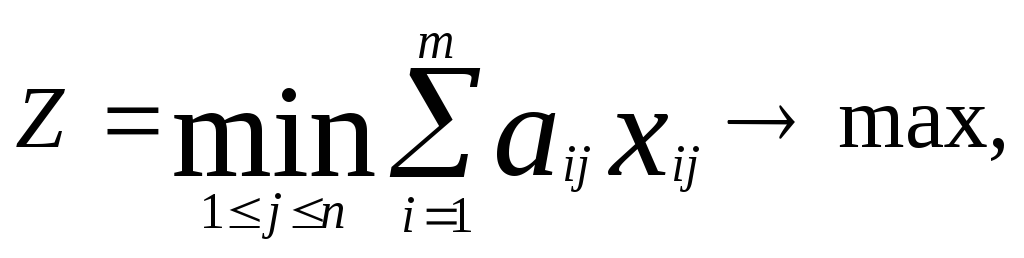 или,
учитывая формулу для Nj,
получаем целевую функцию:
или,
учитывая формулу для Nj,
получаем целевую функцию:
которую требуется максимизировать.
Отличие этой задачи от всех ранее рассмотренных состоит в том, что здесь максимизируемая функция
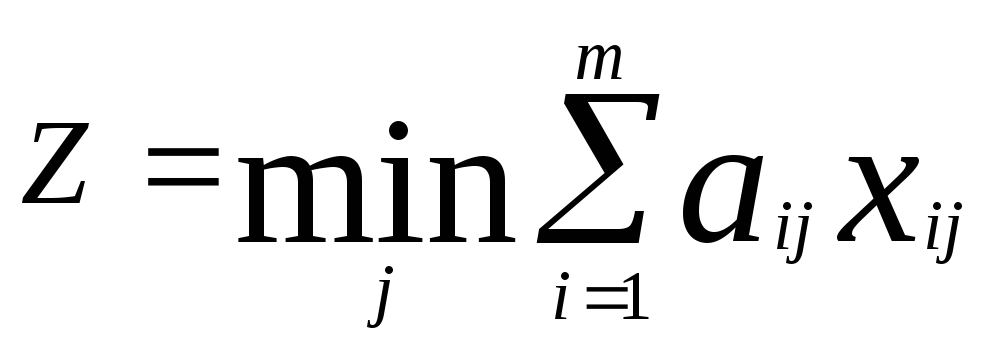
не является линей функцией переменных xij и, таким образом, задача не является задачей линейного программирования. Однако её легко свести к ЗЛП следующим образом.
В![]() ведём
дополнительную переменную y:
ведём
дополнительную переменную y:
Т![]() ак
как величина y является
минимальной из всех величин
ак
как величина y является
минимальной из всех величин
![]() то
можно написать ряд неравенств, связывающую
переменную y с другими
переменными,
то
можно написать ряд неравенств, связывающую
переменную y с другими
переменными,
Т![]() огда
целевую функцию можно представить в
виде
огда
целевую функцию можно представить в
виде
к
 оторую
требуется максимизировать. Но теперь
целевая функция Z=0*x11+…+0*xmn+1*y
является линейной функцией относительно
переменных xij
(i=1,m ; j=1,n)
и y, т. е. математическая
модель стала обычной ЗЛП.
оторую
требуется максимизировать. Но теперь
целевая функция Z=0*x11+…+0*xmn+1*y
является линейной функцией относительно
переменных xij
(i=1,m ; j=1,n)
и y, т. е. математическая
модель стала обычной ЗЛП.
Задачи такого типа, где требуется обратить в максимум минимальное значение какой-то величины(или, наоборот, в минимум – максимальное), довольно часто встречаются на практике и называются "задачами на минимакс". Рассмотренным выше приёмом (введением дополнительной переменной, которая в первоначальной постановке задачи не фигурировала) этот класс задач сводится к обычной ЗЛП.
