9

Практическое занятие № 3 (2 часа)

Тема: Геометрическая интерпретация задач линейного программирования

Рассматриваемые вопросы:

• Знакомство с геометрической интерпретацией задач ЛП в стандартной форме;

• Решение задач ЛП в стандартной форме при n=2 геометрическим способом;

• Геометрическая интерпретация задач ЛП в канонической форме при

n - m=2 и её геометрическое решение.

1. Геометрическая интерпретация ЗЛП в стандартной форме

Область доступных решений ЗЛП в стандартной форме образуется перечислением m множеств. Каждое из них определяется соответствующим неравенством

a_i1x₁+…+ a_inx_n  b_i , i=(1)

и представляет собой полупространство, лежащее по одну сторону от гиперплоскости

a_i1x₁+…+ a_inx_n = b_i , i=(2)

Пересечение указанных полупространств является многогранником, который и будет областью допустимых решений задачи и обозначается как X.

Линии уровня минимизируемой функции

z = с₁x₁+…+c_nx_n = const (3)

образуют семейство параллельных плоскостей. Вектор нормали к этим плоскостям

c = {c₁, c₂, …, c_n}^T

определяет направления возрастания нулевой функции z, а противоположный вектор –с определяет направление убывания функции z.

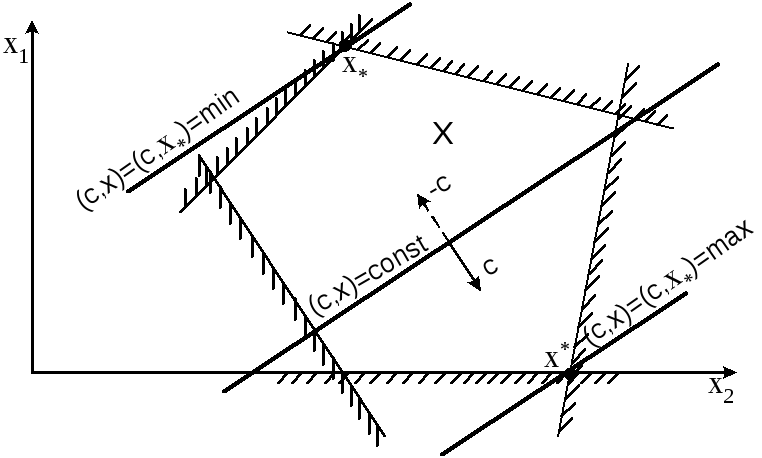Рис1. Геометрическая интерпретация ЗЛП в стандартной форме

Выберем из семейства (3) любую плоскость, пересекающую многогранник допустимых решений X, и будем смещать ее в направлении с, если решается задача максимизации целевой функции z, и в направлении -с , если решается задача минимизации. Будем смещать эту плоскость до такого предельного положения, когда многогранник Xокажется весь по одну сторону от неё и хотя бы одна их точек X все еще будет принадлежать нашей плоскости. Эти точки, или точка, лежащие на плоскости и будут решением задачи минимизации целевой функции z, и x^* решением, соответственно, задачи максимизации функции z (рис. 1).

Заметим, что множество точек, удовлетворяющих неравенству (1), т.е. множество допустимых решений X, может быть пустым, ограниченным и неограниченным. В первом случае задача не имеет решения.

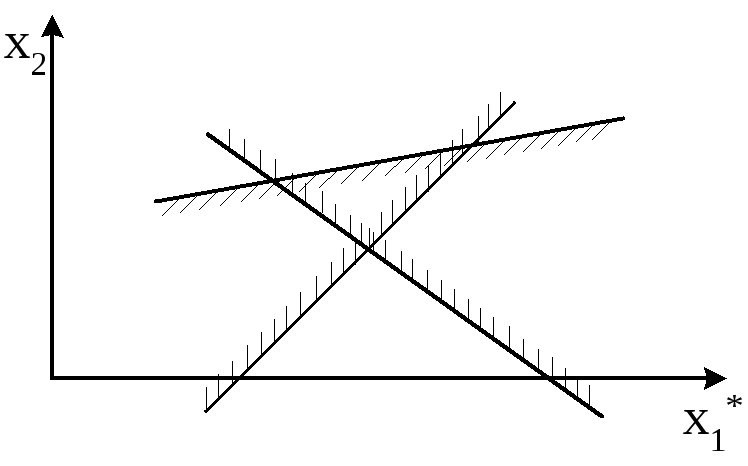
Рис.2 Пример пустой области допустимых решений (X)

Решения X*

Во втором случае ЗЛП заведомо разрешима и имеет либо единственное решение (рис.1), совпадающее с одной из вершин допустимого многогранника X, либо бесконечное множество решений (рис.3) – ребро или грань многогранника, параллельные плоскостям семейства (3).

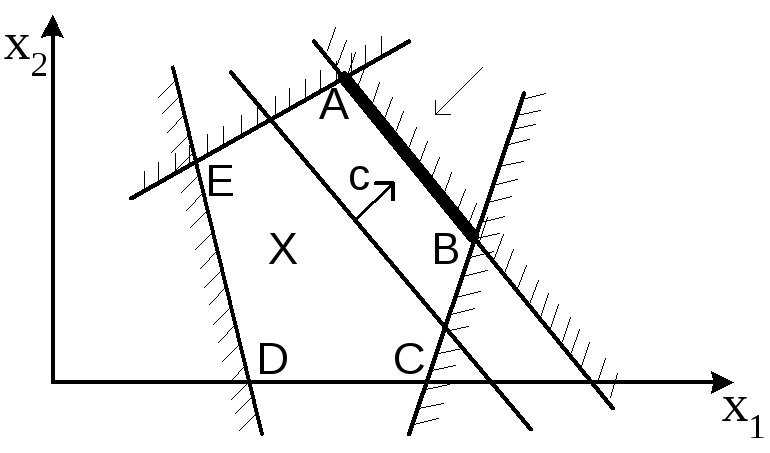
Рис.3 Пример ЗЛП, имеющий бесконечное множество решений (ребро АВ многогранника допустимых решений ABCDE)

Если допустимое множество решений ЗЛП неограниченно, ответ на вопрос о существовании ее решения для задачи максимизации зависит от того, ограничена сверху на этом множестве целевая функция zили нет. Если ограничена, задача разрешима, причем возможны те же ситуации, что и во втором из рассмотренных выше случаев. Если нет – решение отсутствует (рис.4). Для задачи минимизации, в случае неограниченного множества допустимых решенийX, ответ на вопрос о существовании решения ЗЛП

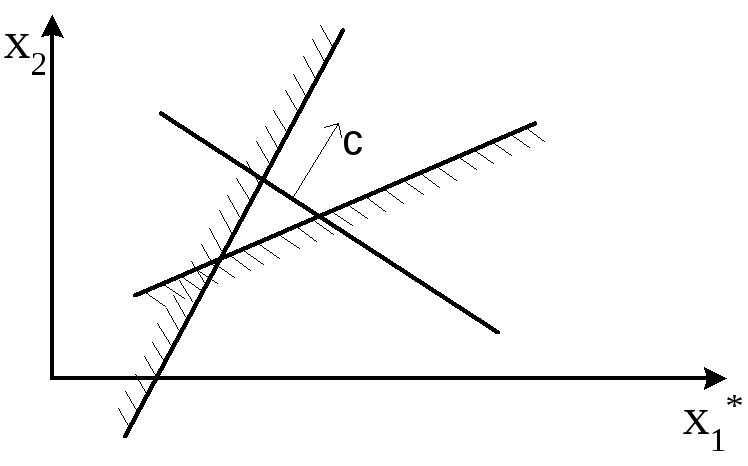
Рис.4 Пример ЗЛП, имеющей неограниченное множество допустимых решений.

зависит от того, ограничена снизу на множестве Xцелевая функцияzили нет. Возникающие ситуации те же что и у задач максимизации.

2. Геометрическое решение ЗЛП в стандартной форме.

Если задача линейного программирования в стандартной форме содержит всего лишь две переменные x₁ и x₂ (т.е. n=2), то ее можно решить следующим способом, основанным на ее геометрической интерпретации.

Каждое неравенство системы ограничений и условие неотрицательности представляют собой полуплоскость. Пересечение полуплоскостей образует выпуклое многоугольное множество (многогранник допустимых решений).

Целевая функция графически изображается множеством параллельных прямых, называемых линиями уровня, каждой из которых соответствует конкретное значение z.

Для решения задачи линия уровня сдвигается в пределах области допустимых решений (многогранника допустимых решений) в направлении вектора-градиента grad z=f(x) = до самой крайней точки области для задачи максимизации , и в направлении антиградиента

• grad z=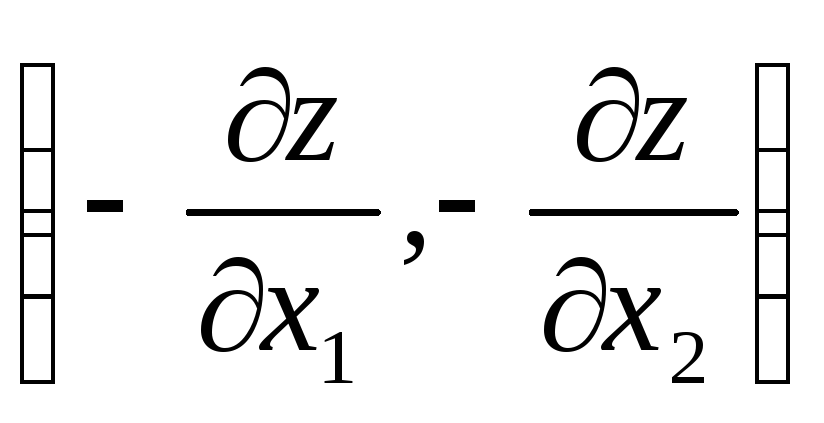для задачи минимизации. Координаты этой

точки и определяют решение ЗЛП (оптимальный план задачи).

Пример 1 Решить геометрическим способом злп:

Z = 6x₁+2x₂  max

4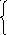x₁+5x₂  61 (a)

-3x₁+4x₂  24 (б)

5x₁-3x₂  30 (в)

x₁ 0, x₂ 0

Решение

Построим область допустимых решений ЗЛП, представляющую собой множество точек, удовлетворяющих ограничениям задачи. Область допустимых решений – ограниченный многоугольник, выделенный внешней

(б)

(в)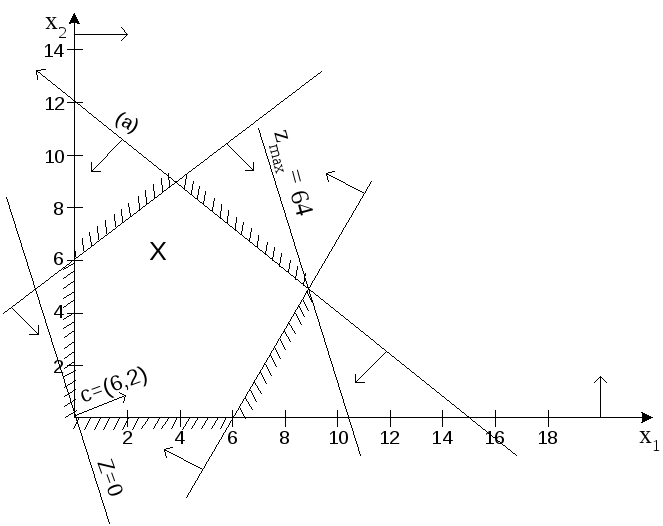

Рис.5 Пример геометрического решения ЗЛП в стандартной форме при n=2.

штриховкой.

Вектор-градиент целевой функции grad z=c={6,2} определяет направление ее возрастания. Из рисунка видно, что целевая функция z принимает максимальное значение в точке пересечения прямых, задаваемых неравенствами (а) и (б):

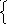4x₁+5x₂ = 61

5x₁-3x₂ = 30

Решив эту системы уравнений, получим x₁^*=9, x₂^*=5. Максимальное значение функции z_max=64.

Пример 2 Решить геометрическим способом ЗЛП:

Z = 8x₁+10x₂  max

x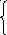₁+2x₂  220 (a)

2x₁+x₂  260 (б)

4x₁+5x₂  640 (в)

x₁ 0, x₂ 0

Решение

Построим область допустимых решений задачи.

(б)

(в)

Р

ис.6 Пример геометрического решения ЗЛП.

Эта область предоставляет собой выпуклый многоугольник ОМ₁М₂М₃М₄. Определим координаты вершин многоугольника, как точки пересечения соответствующих прямых. Координаты вершины М₁ из решения системы

x₁+2x₂=220

x₁=0

Решив эту систему, получим М₁={0;110}. Координаты вершины М₂={60;80}

получим из системы

x₁+2x₂=220

4x₁+5x₂=640

Координаты вершины М₃={110;40} получим из системы

2x₁+x₂=260

4x₁+5x₂=640

Координаты вершины М₄={130;0} получим из системы

2x₁+x₂=260

x₂=0

Из геометрической интерпретации ЗЛП видно, что, если задача имеет решение, то оно достигается в одной из вершин многоугольника допустимых решений. Поэтому для того, чтобы найти решение достаточно перебрать все вершины многоугольника допустимых решений. Вычислим значения целевой функции во всех вершинах этого многоугольника:

z₀ = f(M₀) = 0,

z₁ = f(M₁) = 1100,

z₂ = f(M₂) = 1280,

z₃ = f(M₃) = 1280,

z₄ = f(M₄) = 1040.

Отсюда видно, что целевая функция z достигает максимального значения в двух вершинах М₂ и М₃ , т.е. в своем крайнем положении линия уровня

z = 8x₁+10x₂=const=1280 содержит вершины М₂, М₃ и, следовательно, все ребро (М₂ , М₃). Таким образом, решений бесконечно много – все точки ребра (М₂ , М₃). При этом максимальное значение целевой функции z равно 1280.

Пример 3 Решить геометрическим способом ЗЛП

z=x₁+x₂  max

x₁+x₂  -1 (a)

x₁  0, x₂  0