В этом случае сигнал s(t) может быть представлен в виде:

(5.1)

Соотношение (5.1) представляет собой обобщенный ряд Фурье, где коэффициенты, - функции, называемые базисными функциями, должны быть непрерывны в области определения , и удовлетворять условию ортогональности.

(5.2)

в (5.2) 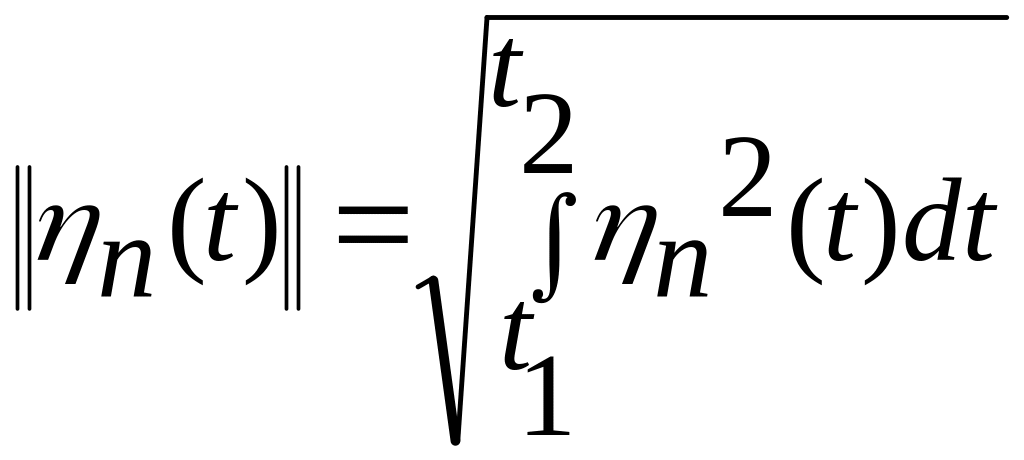-норма функции ;

 некоторое постоянное число.

Если , базисную функцию называют ортонормированной.

Найдем коэффициент , для чего представим (5.1) следующим образом: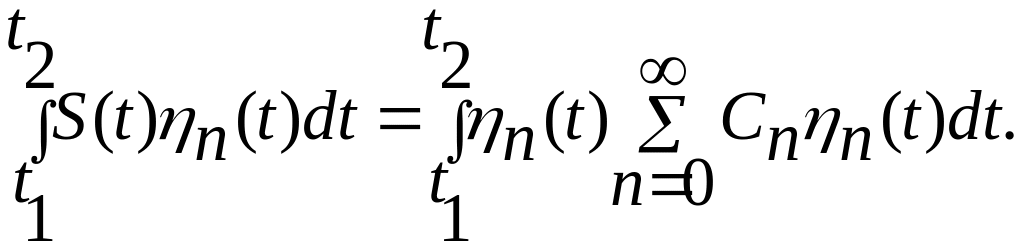 (5.3)

т.к. все члены суммы в правой части вида при равны нулю, (5.3) будет иметь вид:

,

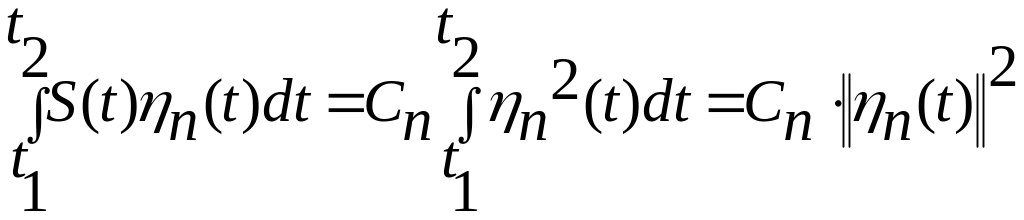откуда 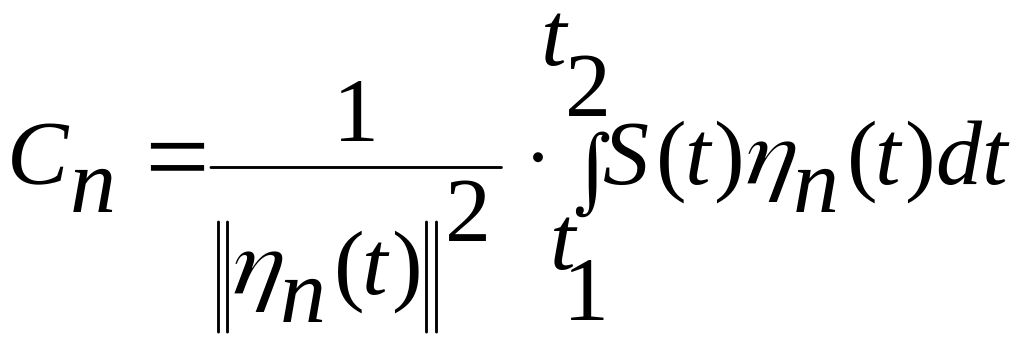- коэффициент обобщенного ряда Фурье.

При усечении числа членов ряда (5.1) до N имеет место погрешность представления сигнала S(t) в виде ряда и можно показать, что:

(5.4)

Это неравенство Бесселя.

Если -величина комплексная, то

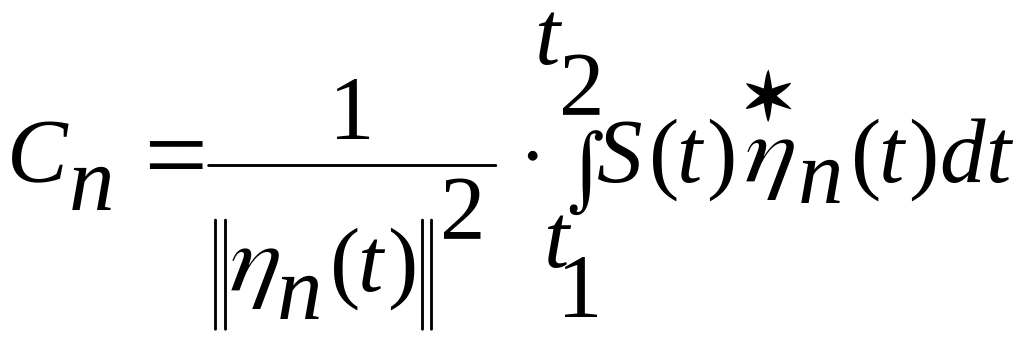(5.5)

* - знак сопряженной величины и .

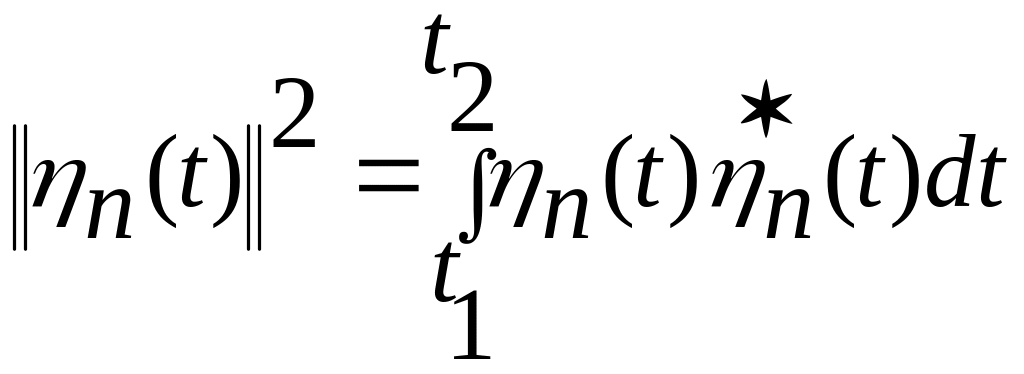Рассмотрим энергетические соотношения при разложении сигнала в обобщенный ряд Фурье.

Энергия электрического сигнала , заключенная в интервале , выражается соотношением:

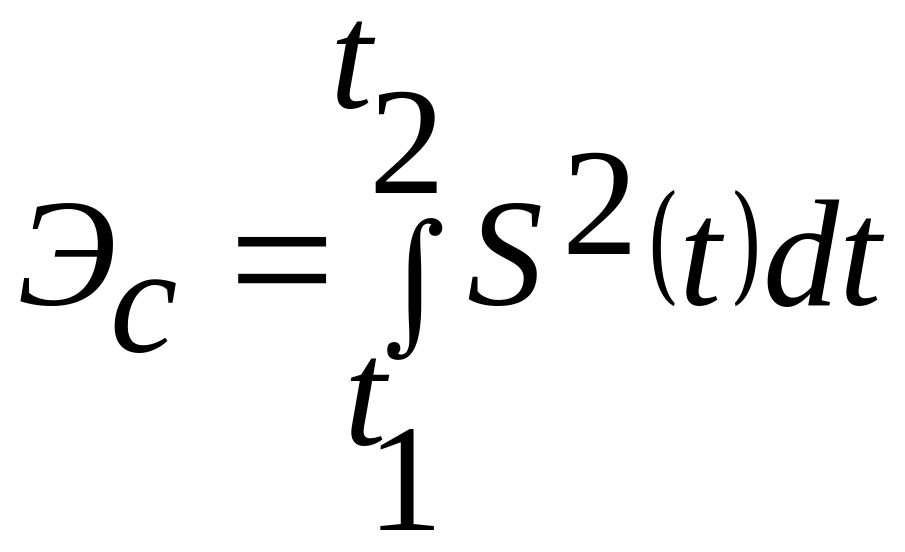(5.6)

-энергия, выделяемая на сопротивление в 1 Ом за время .

Соответственно ; мощность сигнала.

Устремляя в соотношении (5.4) , можем сделать ошибку усечения ряда в пределе сколь угодно малом и получим равенство:

(5.7)

Это равенство Парсеваля.

Если то (5.8)

Соотношение (5.8) свидетельствует о том, что полная энергия сигнала в интервале при разложении его в обобщен­ный ряд Фурье равна .

В качестве базисных функций, как было показано выше, может быть использована любая ортогональная система функции. Таких функций известно множество, однако, в технике связи и автоматики использу­ются гармонические функции, а также ряд специальных функций: Лагерра, Лежандра, Уолша, Бесселя и др.

Выбор базисной функции произ­водится из соображений:

1. Минимизации числа членов ряда N при достижении заданной точности представления сигнала обобщенным рядом Фурье. 2. Простотой аппаратурной реализации генерирования базисной функции.

5.2. Разложение сигнала в базисе гармонических функций

5.2.1. Экспоненциальный ряд Фурье

Пусть сигнал определен на интервале 0t и является периодическим:

n=0, 1, 2, 3…

В качестве базисной функции возьмем экспоненциальную функции вида ,где .

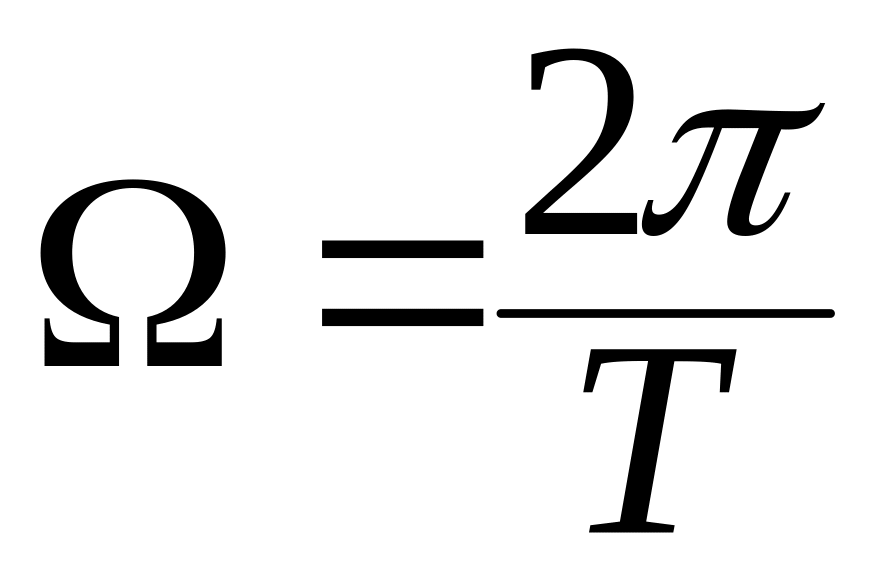Запишем ряд Фурье (5.1) в виде: (5.9)

Это экспоненциальный ряд Фурье.

Для вычисления необходимо найти , а также следует убедиться в том, что данная базисная функция удовлетворяет условию ортогональности.

Легко показать также, что при .

В самом деле:

Отметим еще раз, что Tпериод колебания. Учитывая сказанное, получим выражение для в виде:

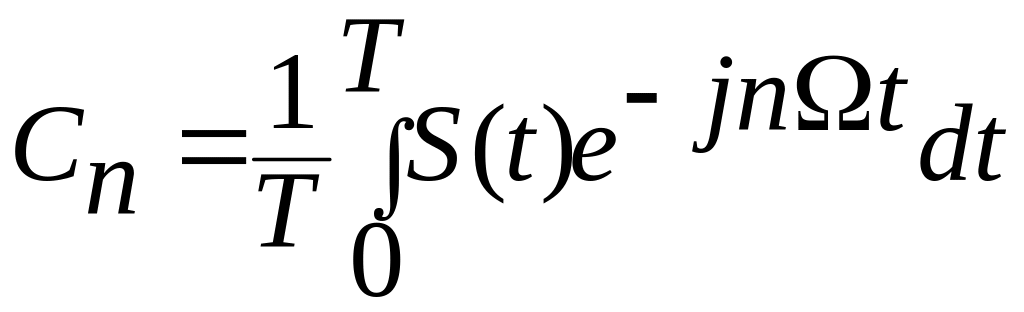(5.10)

5.2.2. Тригонометрический ряд Фурье

В инженерной практике чаще используется тригонометрическая

фор­ма ряда Фурье.

Из (5.10) следует, что величина в общем слу­чае комплексная и может быть представлена в виде:

; ;

Запишем (5.9) в виде:

Суммируя по обе стороны 0-ые члены с одинаковыми индексами и учи­тывая, что , имеем

(5.11)

(5.11)- тригонометрическая форма ряда Фурье.

Представив

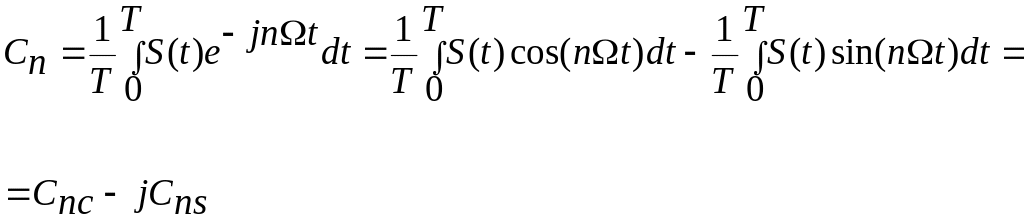
и обозначив

получим следующую модификацию тригонометрического ряда:

. (5.12)

Заметим, что

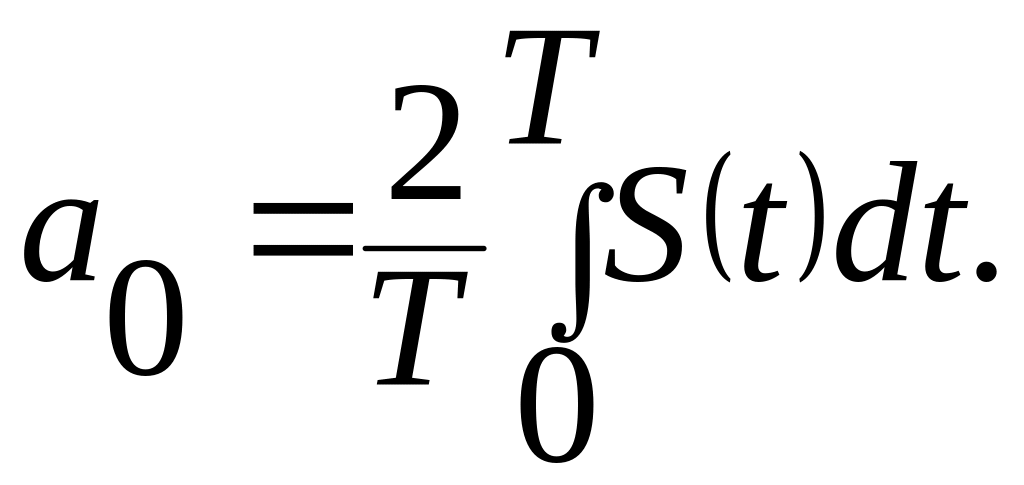
Разложение сигнала в ряд (5.9) и (5.12) представляет сигнал в виде вектора в многомерном пространстве, где члены ряда есть про­екции вектора на координатные оси x, y, z,… Координатные оси - орты и есть базисные функции.

В данном случае или .

ПРИМЕР 5.1

Разложить сигнал (рис.5.1),представляющий собой периодическую последовательность прямоугольных импульсов, в экспоненциальный ряд Фурье. Длительность импульса , амплитуда U, период T.

Рис. 5.1

Вычислим коэффициенты ряда:

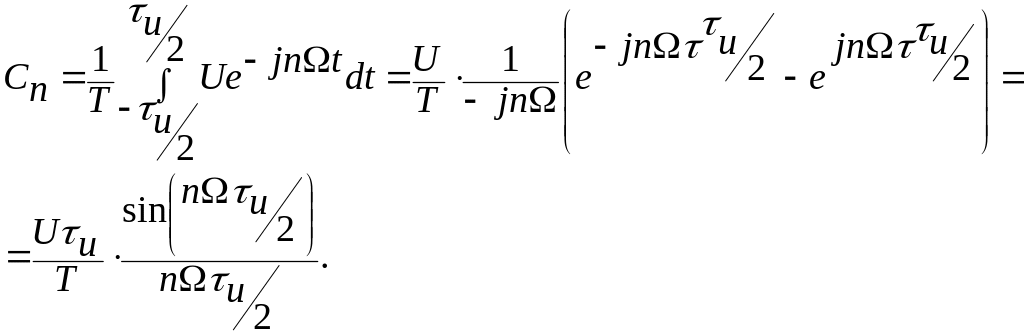
sinc x 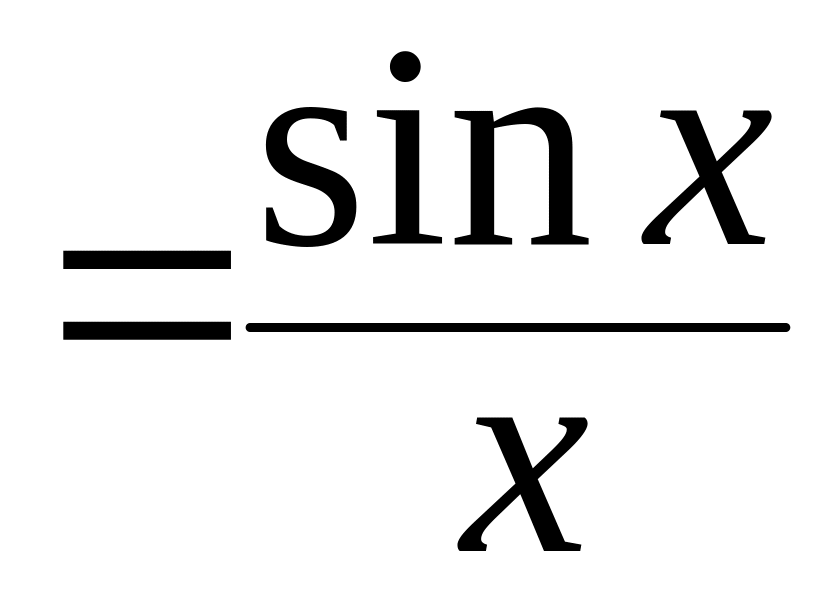-интегральный синус ;

.

Подставив , получим: .

Учитывая, что sinc x функция четная: sinc x=sinc(-x) запишем экспоненциальный ряд Фурье в виде: .

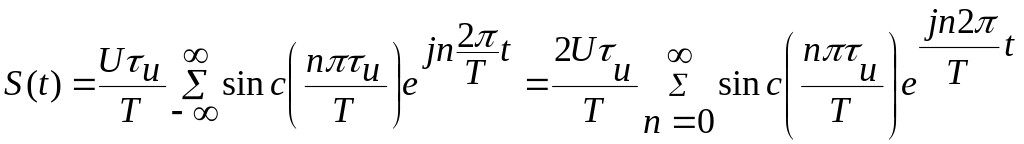5.3. Спектр периодического сигнала

Множество называется комплексным спектром периодического сигнала.

Множество составляет амплитудный спектр.

Множество составляет фазовый спектр.

Рассмотрим картину спектра периодической последовательности прямоугольных импульсов (см. пример 5.1).

При этом в качестве спектральных составляющих будем брать коэффициенты тригонометрического ряда Фурье, где модуль удваивается.

Рис. 5.2

Отметим, что коэффициент существует только в точках кратных

Рис.5.2 изображает амплитудный спектр заданного сигнала. Пунктирная линия является огибающей амплитудного спектра и равна 0 в точках, где 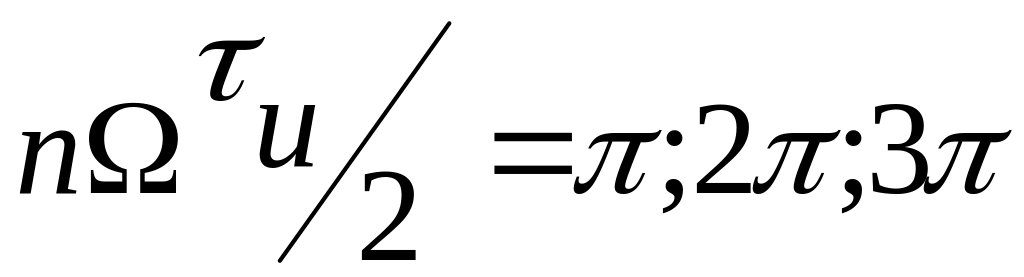и т.д.,отсюда:

…

Частотный интервал заключает в себя первую полуволну огибающей спектра (первый лепесток), - вторую полуволну и т.д.

Фазовый спектр данного сигнала изображен на рис.5.3.

Рис. 5.3

На рис. 5.3 видно, что изменяется ступенчато с интервалом , что связано с периодическим изменением знака .

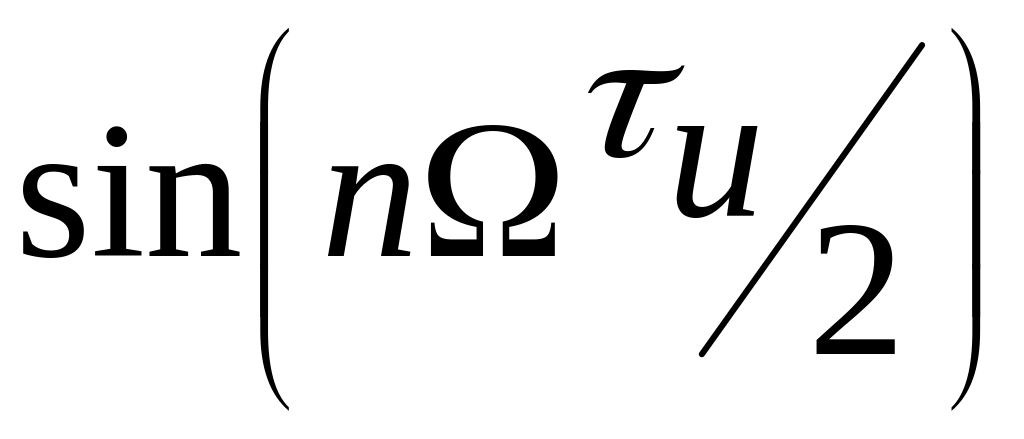ПРИМЕР 5.2

Разложить в тригонометрический ряд Фурье сигнал , представляющий собой знакопеременную периодическую последовательность прямоугольных импульсов  меандр (рис.5.4).Амплитуда сигнала U, период Т.

В соответствии с (5.11):

;

Рис. 5.4

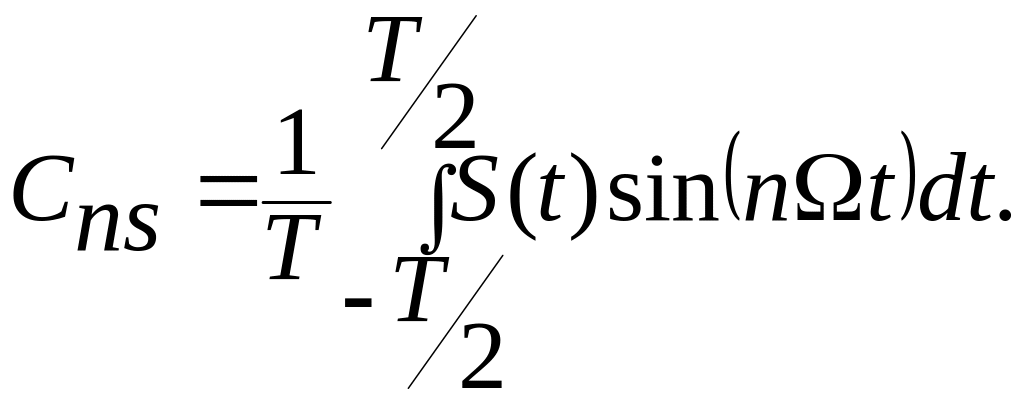
Согласно выбранному началу отсчета функция нечетная и

соответственно равны 0.

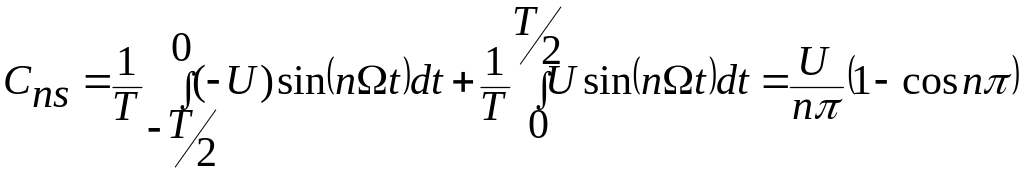
Таким образом, .

(см.п.5.2.2)

Запишем в виде:

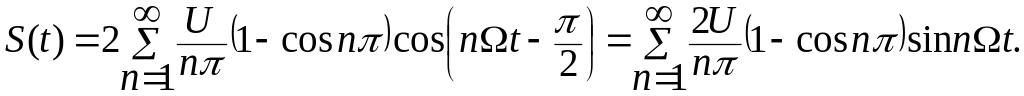
Построим спектральную диаграмму до n=7.

Спектральная диаграмма данного сигнала изображена на рис.5.5.

Рис. 5.5

Легко видеть, что и ряд Фурье имеет вид:

.

Рассмотренный пример позволяет дать прозрачную физическую трак­товку понятию спектра периодического сигнала.

Коэффициенты являются амплитудами мгновенных значений то­ков или напряжений частот ,а -их начальными фазами.

В самом деле:

и т.д.

Суммируя члены ряда Фурье, можно восстановить временную форму сигна­ла.

На примере периодической последовательности равноотстоящих импульсов (Рис.5.1) рассмотрим точность представления сигнала в зависимости от числа членов ряда (Рис.5.6, а, б, в, г, д, е, ж).

Амплитуда импульса U= 1 Вольт

Длительность = 0,1 миллисекунда

Период T= 0,2 миллисекунды

N-число членов ряда.

N =1

а)

N=3

б)

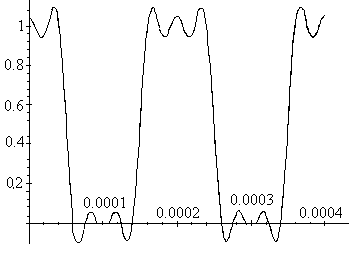
N=5

в)

N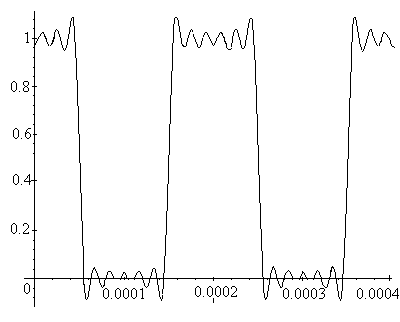 =11

г)

N=21

д)

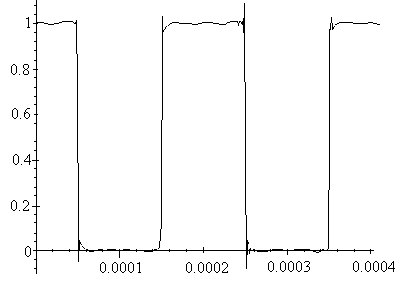
N=101

е)

N =1001

ж)

Рис. 5.6

Разложение в ряд Фурье периодических сигналов позволяет решить, по меньшей мере, две практически важные задачи:

1.Определение с достаточной для инженерной практики точностью ширины спектра сигнала.

Хотя ряд Фурье бесконечен, можно брать конечное число членов ряда, оговорив заранее ошибку "усечения" ряда.

В соответствии с равенством Парсеваля,

(5.13) Используя принятый в практике критерий, что ошибка "усечения" ряда не должка быть больше 0,1 и на основе (5.13) запишем:

. (5.14)

и, таким образом, верхняя ширина спектра сигнала .

2. Синтез сигнала заданной формы.

Задан спектр сигнала в обобщенном базисе .

Необ­ходимо аппаратурным путем синтезировать данный сигнал, т.е. восста­новить его временную форму .

Принцип действия синтезатора сигнала в обобщенном базисе поясняется на рис.5.7.

Рис. 5.7

Как уже упоминалось выше, необходимое число членов ряда для достижения заданной точности совпадения и зависит от вида базисной функции .

5.4. Спектр непериодического сигнала

Предельным случаем периодического сигнала является одиночный

с игнал: импульс, "пачка" импульсов и т.д. (рис.5.8,а,б,в).

Рис. 5.8

Для вычисления спектра непериодического сигнала предположим, что сигнал периодический с (рис. 5.9),

Рис. 5.9

и используем это предположение для получения аналитического вы­ражения спектра данного сигнала.

Запишем для экспоненциальный ряд Фурье:

(5.15)

где

(5.16)

Учитывая (5.15), (5.16) и полагая, что при

а - текущая частота, преобразуем сумму бесконечно малых величин в интеграл.

Запишем: 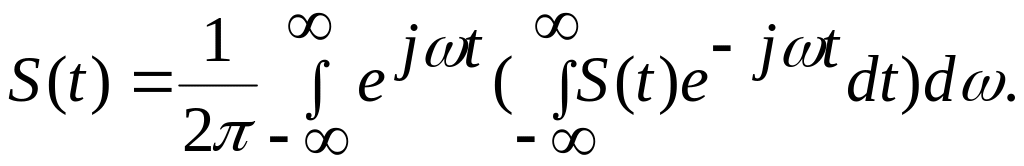(5.17)

Введем обозначение:

(5.17а)

Тогда (5.17) примет вид:

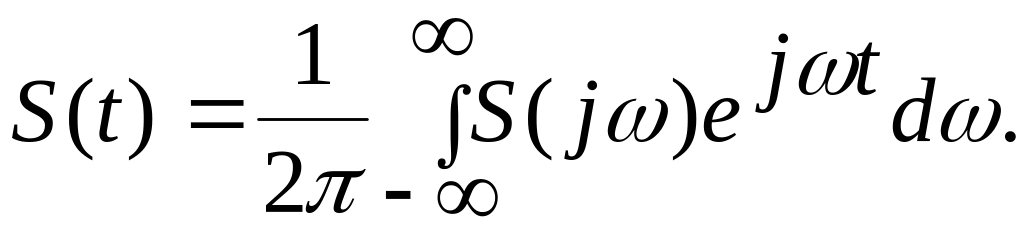(5.18)

Выражения (5.17а) и (5.18) представляют собой соответственно формулы прямого и обратного преобразования Фурье. В литературе для указанных преобразований приняты следующие условные

обозначения:

,

- является непрерывной функцией частоты и представляет собой спектральную плотность сигнала.

В дальнейшем спектральную плотность будем называть спектром.

В общем случае величина - комплексная и может быть представлена в виде:

,

где

- спектральная плотность амплитуд-ампли­тудный спектр;

- спектральная плотность фаз - фазовый спектр.

ПРИМЕР 5.3

Вычислить спектр одиночного прямоугольного импульса(рис.5.10).

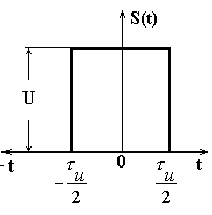
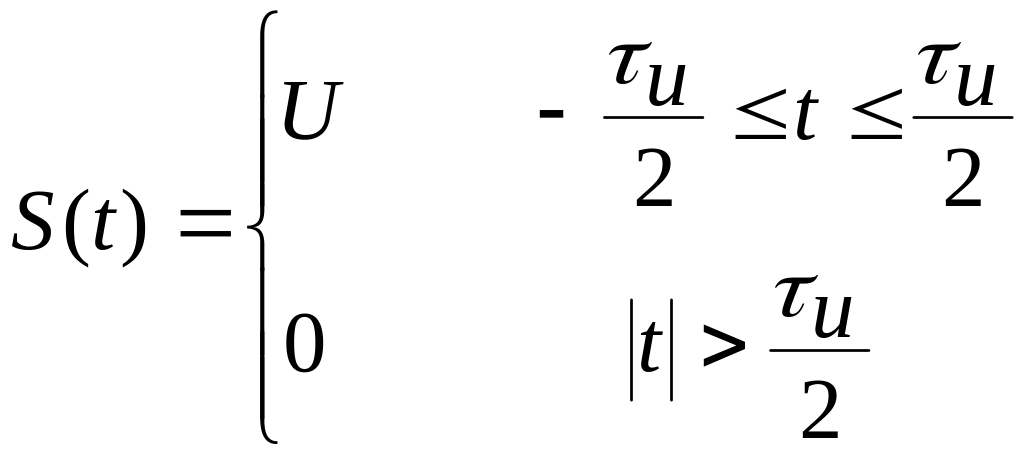
Рис. 5.10

А мплитудный и фазовый спектры изображены на рис.5.11,а,б.

Рис. 5.11

Основные свойства спектра непериодического сигнала.

1.Спектр непериодического сигнала сплошной - непрерывная функ­ция .

2.Размерность спектра непериодического сигнала: [размерность сигнала ].

Таким образом, спектр непериодического сигнала можно трактовать, как плотность амплитуд мгновенных значений тока или напряжения на единицу частоты.

3.Кривая спектра непериодического сигнала совпадает с огибаю­щей спектра периодического сигнала такой же формы с учетом мас­штабного коэффициент.

Сравнительная характеристика спектров периодического и неперио­дического сигналов.

Периодический сигнал

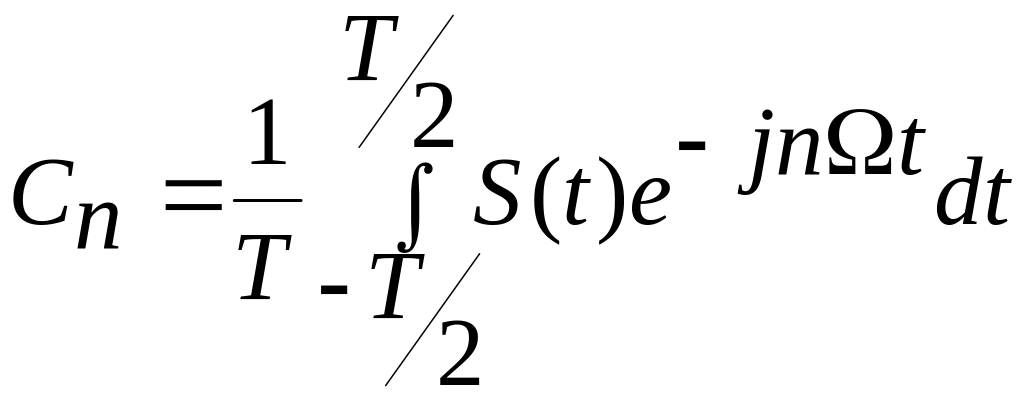
-дискретная функция .

Непериодический сигнал

; -непрерывная функция .

Огибающие и совпадают (с точностью до масштабного коэффициента) (рис.5.12,а,б).

Рис.5.12

Физический смысл:

- амплитуда мгновенного значения колебания тока или напряжения частоты .

- плотность амплитуд тока или напряжения на единицу частоты.

5.5. Основные теоремы о спектрах

5.5.1. Теорема линейности

Спектр суммы сигналов равен сумме спектров слагаемых сигналов.

Доказательство:

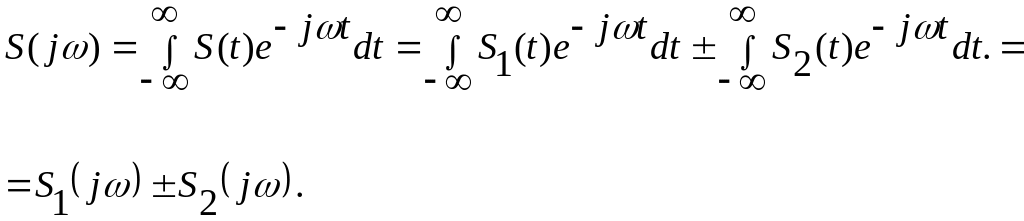
Следствие: если ,то .

Иногда данное следствие называют теоремой пропорциональности.

5.5.2. Теорема запаздывания

Спектр сигнала, запаздывающего на фиксированное время

(рис. 5.13), равен спектру исходного сигнала, умноженного на .

Рис. 5.13

Доказательство:

Производим замену переменных интегрирования:

Представляя и в показательной форме и выделяя модуль и фазу, получим:

Отсюда следует важный вывод, что при передаче сигнала по неискажающей (идеальной линии) имеет место только запаздывание сигна­ла, определяемое временем его распространения вдоль линии , при этом модуль спектра сигнала остается без изменения, а фазовый сдвиг изменяется на величину , т.е. прямо пропорционально

5.5.3. Теорема сжатия (изменения масштаба)

При изменении длительности сигнала в раз модуль и аргумент комплексного спектра изменяются обратно пропорционально .

Пусть (при - имеет место сжатие сигна­ла,

при - расширение сигнала), тогда .

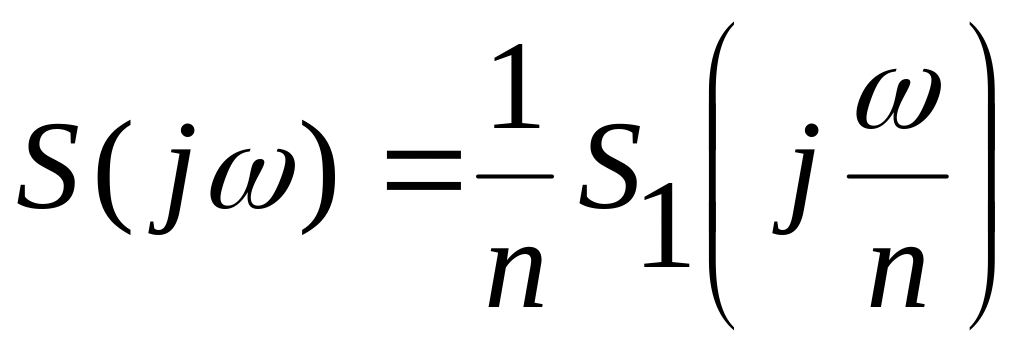Доказательство:

Произведя замену переменных

,

получим:

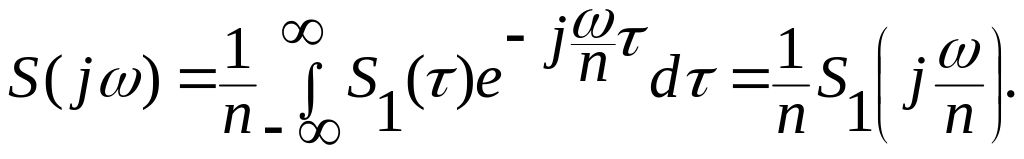
Из данной теоремы следует практически важный вывод: при сжатии сигнала спектр его расширяется прямо пропорционально коэффициенту сжатия, а модуль уменьшается в раз.

5.6.4. Теорема о спектре произведения двух сигналов (теорема свертки)

Спектр произведения двух сигналов равен свертке этих сигналов.

Пусть

тогда (5.19)

Правая часть выражения (5.19) называется интегралом свертки функций и и имеет специальное обозначение:

.

Доказательство:

(5.20)

Представим в виде:

и положим

Тогда соотношение (5.20) примет вид:

Учитывая, что

Запишем в виде:

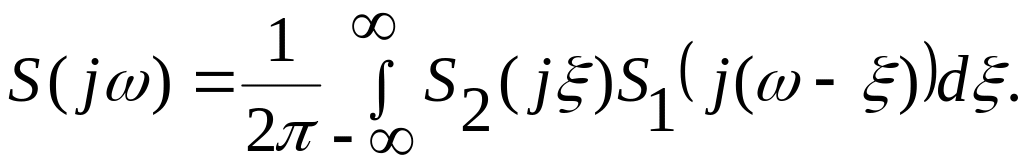(5.21)

Соотношение (5.21) и представляет собой свертку спектров сигналов и .

Аналогично можно показать, что, если то

т.е. произведению спектров двух сигналов соответствует свертка их временных функций.

Из теоремы свертки следует очень важный вывод:

положив в (5.21) и заменяя на , получим

(5.22)

Если , то

- полная энергия сигнала.

Tогда, учитывая (5.22), можно записать:

Так как функция четная относительно ,

то - равенство Парсеваля.

5.5.5 Теорема дифференцирования

(Доказательства теорем п.п. 5.5.5 и 5.5.6 см.,например,в [4]).

Если при , т.е. имеет затухающий с течением времени сигнал,

то при .

5.5.6. Теорема интегрирования

Если , то

5.6. Спектры некоторых типовых сигналов

5.6.1. Спектр единичной функции включения

.

Интеграл в правой части не определен, так как функция в бесконечности не определена.

Применим следующий искусственный прием: представим заданный сигнал в виде ;

- некоторая фиксированная постоянная, которую затем устре­мим к нулю.

И так, для единичного скачка при (см. рис. 5.14), однако, для функция снова не определена.

Рис. 5.14

Определим в точке .

Представим в виде:

(5.23)

Первое слагаемое (5.23) равно 0 при и, одновременно, при обращается в , но мы можем вычислить площадь функции, которая при всех значениях - постоянная величина.

В самом деле:

.

Для фиксации площади в точке умножим полученный резуль­тат на

Таким образом, окончательно:

.

Данное выражение характеризует спектральную плотность сигнала во всей области частот: .

5.6.2. Спектр единичного импульса

,(*)

*- см.фильтрующее свойство - функции.

На рис. 5.15 изображен график спектра

Рис. 5.15

Итак, модуль спектра единичного импульса равен единице в пре­делах и энергия спектра в соответствии с равенством Парсеваля равна , что еще раз свидетельствует о том, что единичный импульс является математической идеализацией и техниче­ски реализован быть не может.

Смещенный на единичный импульс.

, (*)

*-см. теорему запаздывания.

Используя обратное преобразование Фурье (5.18), получим весь­ма полезное соотношение:

. (5.24)

В самом деле:

5.6.3 Спектр сигнала, умноженного на экспоненту

.

5.6.4. Спектр экспоненциального сигнала

Как было показано в п.п.5.6.2,

,

произведя в (5.24) замену , получим

. (5.25)

Выражение (5.25) используется для определения спектра гармонического сигнала.

5.6.5. Спектр гармонического сигнала

Напоминаем, что

Рис.5.16

Можно показать также, что, если , то .

Итак, спектр гармонического колебания дискретный и содержит две составляющие: -(см.рис. 5.16).

Рассмотренные выше спектры типовых сигналов позволяют решать задачи, связанные с вычислением спектров сложных сигналов.

ПРИМЕР 5.4

Вычислить спектр тонального телеграфного импульса (рис. 5.17).

Рис. 5.17

- огибающая гармонического колебания - прямоугольный им­пульс с амплитудой и длительностью (на рис.5.17 огиба­ющая изображена пунктирной линией).

Вычислим спектр огибающей:

,

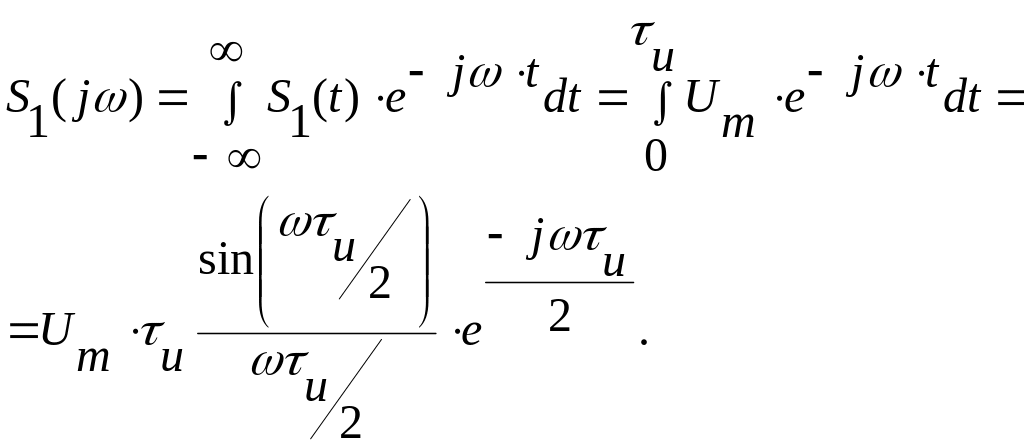
Используя результаты п.5.6.3, можем непосредственно записать:

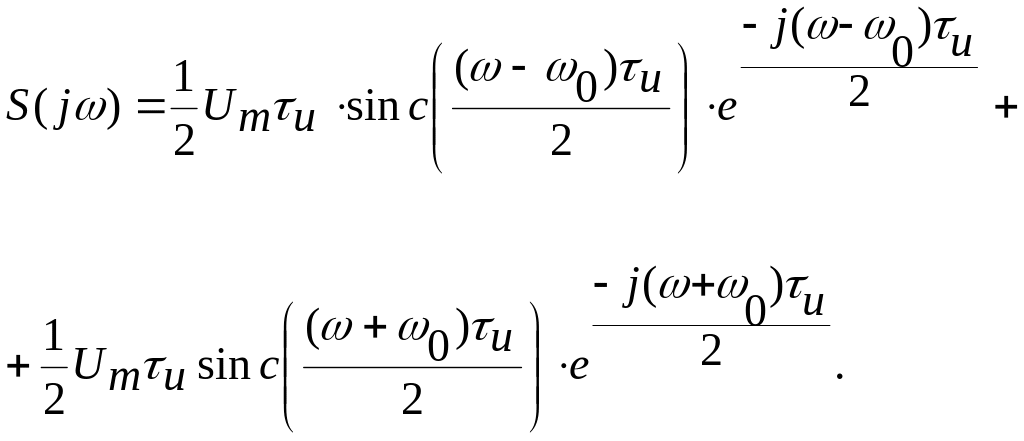
М одуль спектра сигнала изображен на рис.5.18.

Рис. 5.18

Из рис.5.18 видно, что умножение сигнала на гармоническое

колебание с частотой переносит его спектр на частоту вдоль оси , при этом и зеркальное отображение спектра исходного сигнала или часть его (в зависимости от величины ) оказывают­ся в области положительных частот, т.е. спектр может быть в 2 ра­за шире при .

ПРИМЕР 5.5

Вычислим спектр амплитудно-модулированного АМ колебания при мо­дуляции монохроматическим сигналом с частотой .

М - коэффициент модуляции; - модулирующая частота, -несущая частота. Разложим на составляющие:

Используя результаты п.5.6.5, запишем спектр заданного сигна­ла в виде:

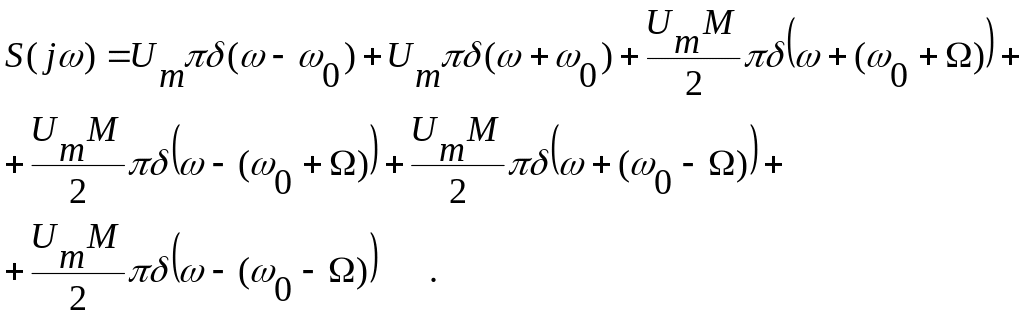
М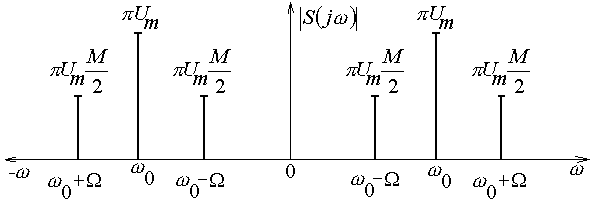 одуль спектра АМ колебания изображен на рис.5.19.

Рис. 5.19

"Зеркальная" часть спектра в области отрицательной частоты фи­зического смысла не имеет, но ее необходимо учитывать при перехо­де к временной форме, используя обратное преобразование Фурье.

ПРИМЕР 5.6

Вычислить спектр пакета равноотстоящих импульсов (рис. 5.20).

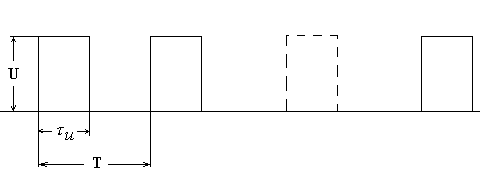
Рис. 5.20

- амплитуда импульсов, - длительность, - межимпульсный интервал, - число импульсов в пакете.

Спектр данного сигнала получим, используя известное выражение для спектра одиночного прямоугольного импульса, теоремы запазды­вания и сложения.

Обозначив спектр одиночного прямоугольного импульса ,получим:

(5.26)

Легко видеть, разлагая по формуле Эйлера на и , что на частотах , где К = 0,1... все слагаемые в скобках (5.26) равны единице и

На частотах выражение в скобках обращается в нуль. Во всех остальных точках имеет место геометрическая сумма слагаемых.

График модуля спектра при изображен на рис.5.21.

Рис. 5.21

На рис.5.21 пунктирной линией нанесена огибающая спектра оди­ночного импульса.

При увеличении пики спектральной функции увеличиваются и сужаются, и при очень большом сплошной спектр вырождается в дискретный, что логично, так как уже будет почти периодиче­ским сигналом (см. рис.5.22).

Рис.5.22

5.7. Частотный (спектральный) метод анализа линейных цепей

Реализация частотного метода базируется на представлении сигна­ла в виде его спектральной функции и использует частотную функцию цепи.

Суть спектрального метода заключается в следующем: спектральная функция отклика равна произведению спектральной функции воздействия на частотную функцию цепи :

(5.27)

Доказательство:

в соответствии с представлением электрической цепи, как динамической системы, отклик и воздействие связаны диф­ференциальным уравнением:

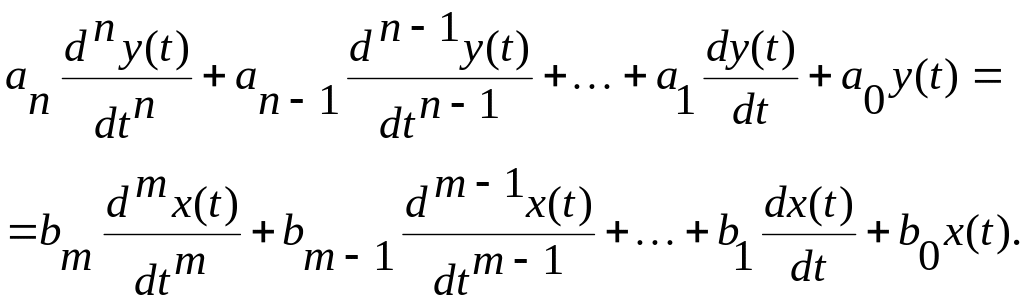(5.28)

- отклик; - воздействие; коэффициенты отражают параметры и конфигурацию цепи.

Применив к правой и левой части (5.28) операцию прямого преобразования Фурье и учитывая тео­ремы сложения и дифференцировании, получим:

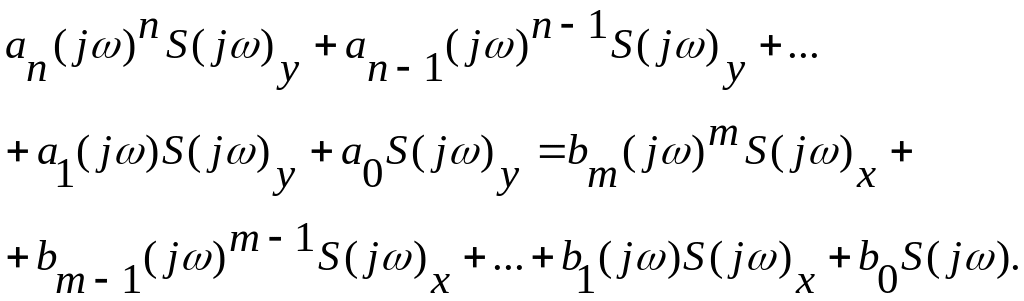(5.29)

Преобразуем (5.29)

(5.30)

обозначим сомножитель:

и окончательно запишем (5.30) в виде:

(5.31)

Соотношение (5.31) является формулой частотного (спектрального) метода анализа отклика линейной цепи на заданное воздействие. Вре­менная форма отклика может быть получена с помощью обратного пре­образования Фурье:

(5.32)

ПРИМЕР 5.7

Определить отклик цепи (рис.5.23) на заданный сигнал:

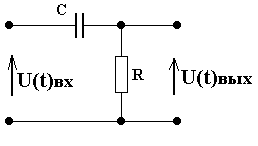
Рис. 5.23

1.Вычислим

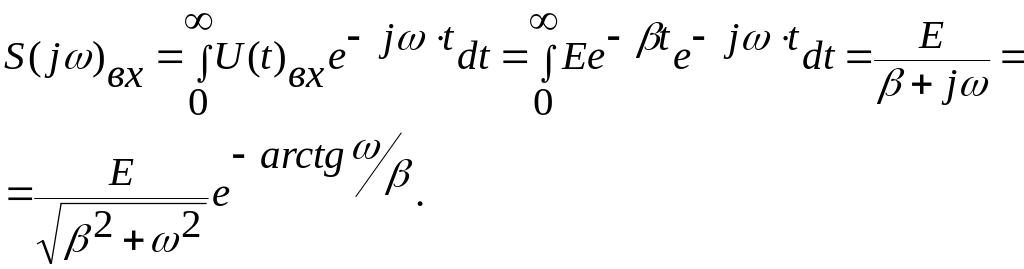
2. Вычислим частотную функцию цепи:

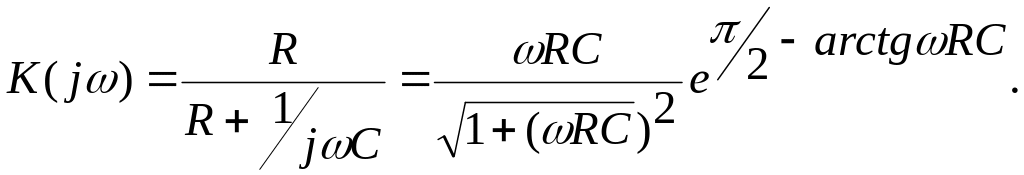
3. Вычислим

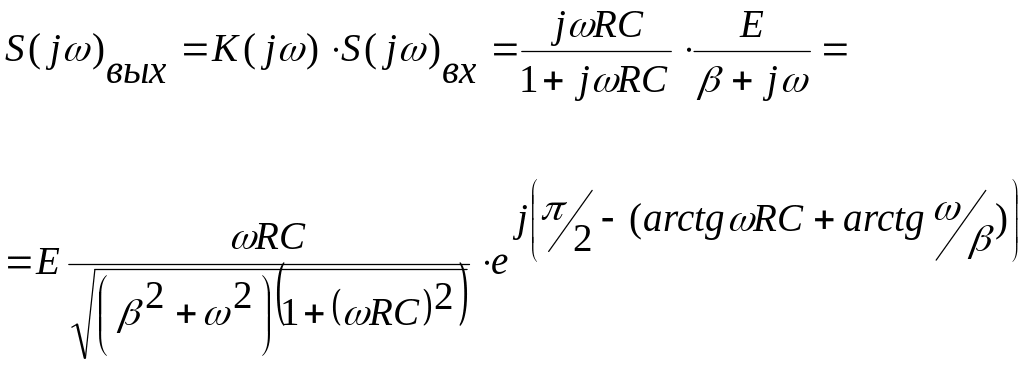
Как уже упоминалось выше, дает возможность отве­тить на ряд вопросов, важных с технической точки зрения: ширина полосы выходного сигнала, степень искажения и др.

Однако можно определить и временную форму отклика:

Вычисление полученного интеграла модно упростить, используя связь между преобразованием Фурье и преобразованием Лапласа.

Заменим на , тогда:

,

для перехода к оригиналу используются, например, таблицы преобра­зования Лапласа, формула разложения или теорема вычетов.

Приведем полученное изображение к табличному виду, в результа­те получим:

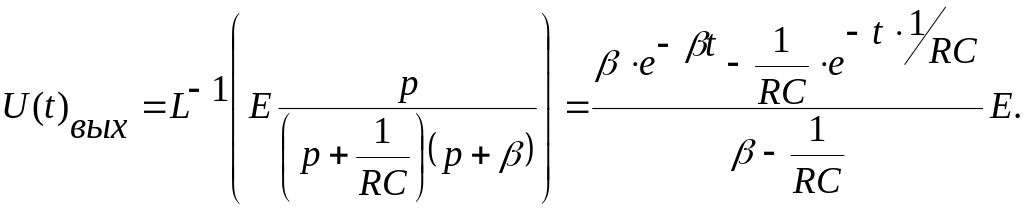
Путем несложных алгебраических преобразований данное выражение приводим к следующему виду:

Активная длительность импульса и эффективная ширина спектра сигнала.

Активная длительность заданного импульса определяется как интервал времени, в котором сосредоточена основная часть энергии сигнала (90-95%), т.е. активная длительность может быть опреде­лена соотношением:

Эффективная ширина спектра сигнала определяется ,как интервал частот, в котором сосредоточена основная часть энергии сигнала (90-95%) и в соответствии с теоремой Парсеваля опре­деляется соотношением:

.

(предполагается, что ; -нижняя частота спектра).

Для сигналов, энергия которых сконцентрирована в ограниченном интервале частот - прямоугольный, колокольный импульсы и др., вводит­ся постоянная ,где - принятая ширина полосы сигнала; - активная длительность импульса.

Для технически реализуемых импульсов колеблется в интервале 0,5 ~ 1, что может служить критерием при оценке ширины полосы при заданной длительности импульса, однако в ряде специальных случаев, например в измерительной технике, ког­да нужно воспроизвести форму сигнала с высокой точностью, бе­рется больше единицы.

5.8. Условие неискаженной передачи сигналов в линейной цепи

Сигнал передается линейной цепью без искажений, если не изме­няется его временная , а следовательно, и частотная формы.

Неизбежными являются только запаздывания сигнала при прохождении через линейный четырехполюсник, например длинную линию, и измене­ние его уровня за счет затухания или усиления.

Таким образом, линейная цепь является неискажающей, если

(5.33)

где - некоторый постоянный коэффициент; - время задержки сигнала в цепи.

Рассмотрим требования к АЧХ и ФЧХ цепи, при которых выполняется условие (5.33).

Используем метод спектральной функции:

(5.34)

Для выполнения условия (5.33) в соответствии с теоремой запазды­вания должно соблюдаться равенство:

= (5.35)

Подставляя в левую часть (5.34) выражение (5.35), получим:

отсюда

(5.36)

Итак, для неискаженной передачи сигнала АЧХ (модуль цепи должен быть равен 1, а ФЧХ (фаза ) должна изменяться пропорционально и равна ).

В самом деле, указанные выше требования технически невыполни­мы в широком диапазоне частот, да в этом и нет необходимости, так как ширину полосы сигнала можно ограничить верхней частотой или интервалом частот: , где и -соответственно верхняя и нижняя частоты спектра сигнала.

Кроме того, как было упомянуто выше, в цепи может иметь место затухание или ослабление сигнала, которые не искажают форму сиг­нала, но изменяют его уровень. 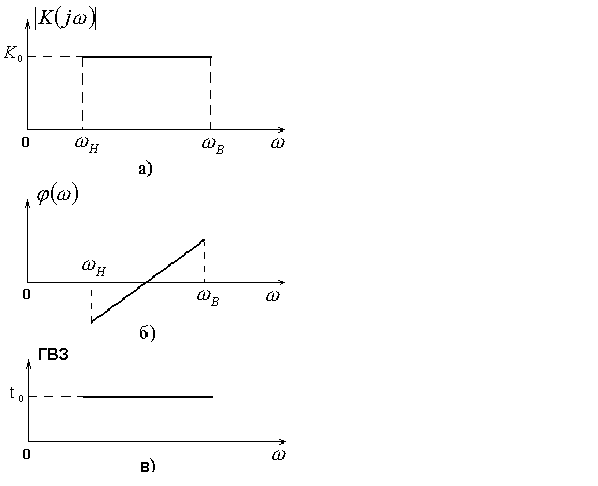Учитывая вышеизложенное, сформули­руем требования к следующим образом: для неискаженной передачи сигнала с полосой, ограниченной в интервале ( ), модуль в заданном интервале частот должен быть равен по­стоянной величине , а фазовая характеристика должна изменяться пропорционально частоте соответственно групповое время запаздывания т.е. времени запаздывания. (рис.5.24,а,б,в)

Рис.5.24

5.9. Связь между временными и частотными функциями цепи

Как было указано выше, временные свойства линейных цепей, характеризующие переходные процессы в них, описываются временными функциями , частотные свойства цепи описываются ее частотной функцией .

Установим связь между частотными и временными функциями линейных цепей на следующем примере:

Подадим на вход линейной цепи (рис.5.25),заданной частотной функцией , единичный импульс и найдем отклик спектральным методом.

Рис.5.25

и соответственно

Учитывая, что по определению, отклик линейной цепи на воздейст­вие единичного импульса равен импульсной функции цепи, можем за­писать, что

а следовательно,

Итак, импульсная и частотная функции цепей однозначно связаны между собой формулами прямого и обратного преобразования Фурье:

; (5.37)

. (5.38)

Установим связь между частотной и переходной функциями цели.

Учитывая, что и используя прямое преобразование Фурье, получаем

(5.39)

ПРИМЕР 5.8

Импульсная функция цепи:

Определим частотную функцию цепи:

.

Применив к обратное преобразование Фурье, запишем:

Для вычисления данного интеграла заменим на и, исполь­зуя связь между преобразованиями Фурье и Лапласа, будем рассматри­вать подынтегральное выражение 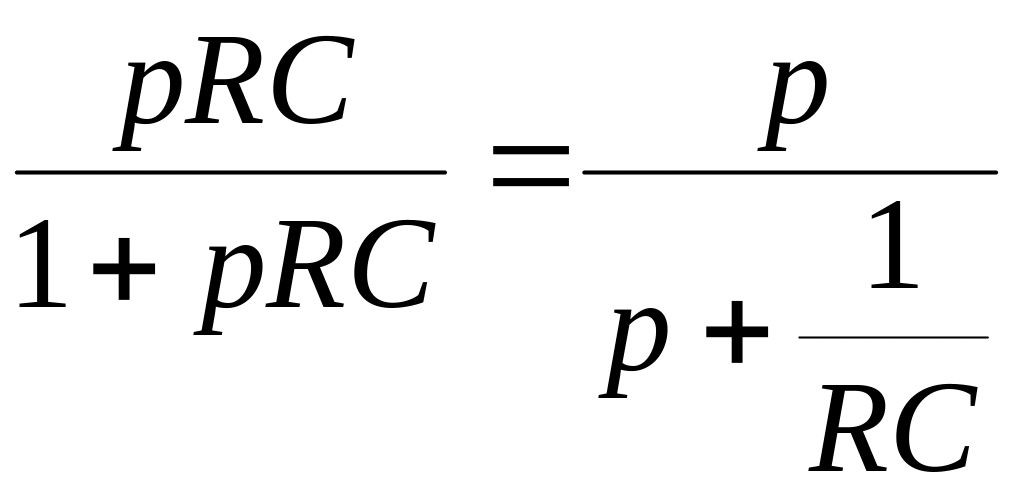как изображение по Лапласу и, переходя к оригиналу, получим: