- •Van der Waals Equation
- •Thermodynamics
- •Internal Energy and the First Law of Thermodynamics
- •Infinitesimal Changes of State
- •19.7 Heat Capacities of an Ideal Gas
- •Restating the Second Law
- •The Carnot Cycle
- •The Carnot Refrigerator
- •Calculating Entropy: Microscopic States
- •Ideal Gases
- •1 Law of Thermodynamics
- •Internal Energy
Kinetic Theory of Gases
Molecules and intermolecular forces. Solids, liquids and gases
The evidence for molecular structure is based on such observations as Brownian motion, diffusion of gases and X-ray diffraction.
All familiar matter is made up of molecules. For any specific chemical compound, all the molecules are identical. The smallest molecules contain one atom each and are of the order of 10-10 m in size; the largest contain many atoms and are at least 10,000 times larger. In gases the molecules move nearly independently; in liquids and solids they are held together by intermolecular forces that are electrical in nature, arising from interactions of the electrically charged particles that make up the molecules. Gravitational forces between molecules are negligible in comparison with electrical forces.
The
interaction of two point
electric
charges is described by a force (repulsive for
like charges, attractive for unlike charges) with a magnitude
proportional to
![]() ,
where
,
where
![]() is
the distance between the points. Molecules
are not
point
charges but complex structures
containing both positive and negative charges, and their interactions
are more
complex. The force between molecules in a gas varies with the
distance
between
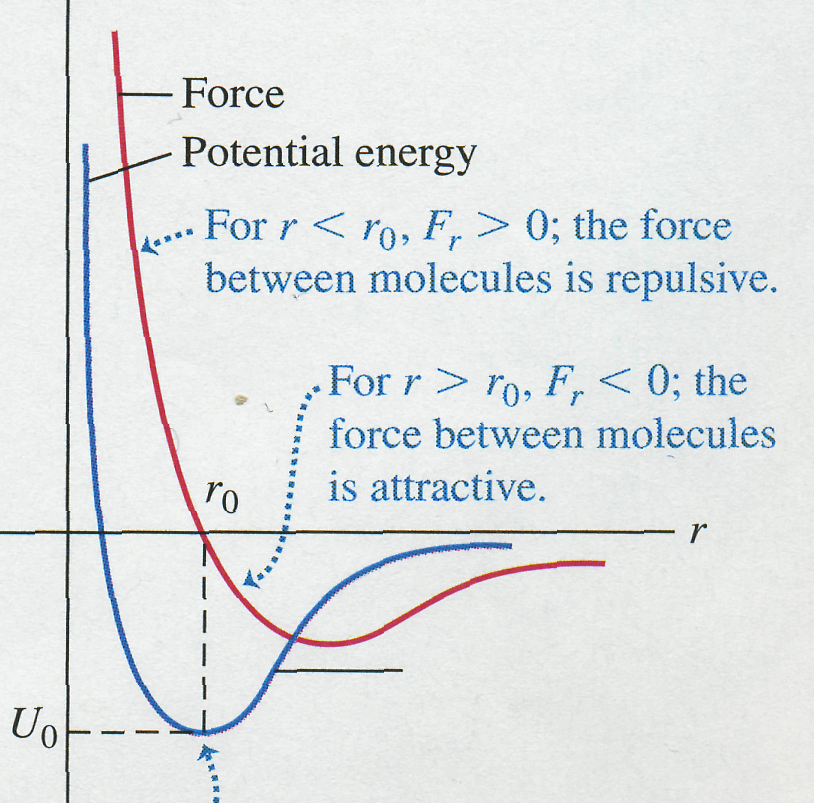
molecules somewhat as shown in Fig. 1, where a positive
is
the distance between the points. Molecules
are not
point
charges but complex structures
containing both positive and negative charges, and their interactions
are more
complex. The force between molecules in a gas varies with the
distance
between
molecules somewhat as shown in Fig. 1, where a positive
![]() corresponds
to a repulsive force and a negative
to
an attractive force. When molecules
are far apart, the intermolecular forces are very small and usually
attractive. As
a gas is compressed and its molecules are brought closer together,
the attractive forces
increase. The intermolecular force becomes zero at an equilibrium
spacing
corresponds
to a repulsive force and a negative
to
an attractive force. When molecules
are far apart, the intermolecular forces are very small and usually
attractive. As
a gas is compressed and its molecules are brought closer together,
the attractive forces
increase. The intermolecular force becomes zero at an equilibrium
spacing
![]() ,
corresponding
roughly to the spacing between molecules in the liquid and solid
states.
In liquids and solids, relatively large pressures are needed to
compress the substance
appreciably. This shows that at molecular distances slightly less
than
the
equilibrium spacing, the forces become repulsive
and
relatively large.
,
corresponding
roughly to the spacing between molecules in the liquid and solid
states.
In liquids and solids, relatively large pressures are needed to
compress the substance
appreciably. This shows that at molecular distances slightly less
than
the
equilibrium spacing, the forces become repulsive
and
relatively large.
Figure 1 |
Figure
1 also shows the potential
energy
as a function of
.
This
function has a minimum
at
,
where
the force is zero. The two curves are related by
![]() .
Such a potential energy function is
often called a potential
well.
A
molecule at rest at a distance
from
a second molecule would need an additional energy
.
Such a potential energy function is
often called a potential
well.
A
molecule at rest at a distance
from
a second molecule would need an additional energy![]() ,
the
"depth" of the potential well, to
"escape" to an indefinitely large value of
.
,
the
"depth" of the potential well, to
"escape" to an indefinitely large value of
.
Molecules are always in motion; their kinetic energies usually increase with temperature. At very low temperatures the average kinetic energy of a molecule may be much less than the depth of the potential well. The molecules then condense into the liquid or solid phase with average intermolecular spacing of about . But at higher temperatures the average kinetic energy becomes larger than the depth of the potential well. Molecules can then escape the intermolecular force and become free to move independently, as in the gaseous phase of matter.
In
solids,
molecules
vibrate about more or less fixed points. In a crystalline solid these
points are arranged in a recurring crystal
lattice. The
vibration of molecules in a solid about their equilibrium positions
may be nearly
simple harmonic if the potential well is approximately parabolic in
shape at distances
close to
.
But
if the potential-energy curve rises more gradually for
![]() than
for
than
for
![]() ,
as
in Fig. 1, the average position shifts to larger
with
increasing amplitude.
This is the basis of thermal expansion.
,
as
in Fig. 1, the average position shifts to larger
with
increasing amplitude.
This is the basis of thermal expansion.
In a liquid, the intermolecular distances are usually only slightly greater than in the solid phase of the same substance, but the molecules have much greater freedom of movement. Liquids show regularity of structure only in the immediate neighborhood of a few molecules. This is called short-range order, in contrast with the long-range order of a solid crystal.
The molecules of a gas are usually widely separated and so have only very small attractive forces. A gas molecule moves in a straight line until it collides with another molecule or with a wall of the container. In molecular terms, an ideal gas is a gas whose molecules exert no attractive forces on each other and therefore have no potential energy.
At low temperatures, most common substances are in the solid phase. As the temperature rises, a substance melts and then vaporizes. From a molecular point of view, these transitions are in the direction of increasing molecular kinetic energy. Thus temperature and molecular kinetic energy are closely related.
The Mole and the Avogadro Constant
The
unit for the amount of a substance is the mole.
It
is defined as the amount of a substance that contains
the
same number of particles (atoms or molecules) as
the
number of atoms in 12 g of the isotope carbon-12.
This
number is known as the Avogadro
constant
(![]() )
and
is
)
and
is
![]() particles
per mole.
particles
per mole.
The
ratio of the mass of one mole of the substance
to
one-twelfth of the mass of one mole of carbon-12
is
called the relative
molecular mass
of
the substance -
it
is 32 for oxygen, 2 for hydrogen and so on. The molar
mass
![]() of a compound is the mass of 1 mole. It is equal to the mass
of a compound is the mass of 1 mole. It is equal to the mass
![]() of a single molecule multiplied by Avogadro’s number:
of a single molecule multiplied by Avogadro’s number:
![]() .
.
A
knowledge of the Avogadro constant enables us
to
calculate the number of molecules in any mass of
a
substance and therefore to get an idea of the size of
one
molecule. For example, a drop of water of volume
![]() =1.0
cm3
has a mass of
=1.0
cm3
has a mass of
![]() =1
g. The relative molecular mass
of
water is 18. To obtain the number of molecules we express mass of the
water as product of mass of one molecular
and the total number of molecules
=1
g. The relative molecular mass
of
water is 18. To obtain the number of molecules we express mass of the
water as product of mass of one molecular
and the total number of molecules
![]() :
:
![]() and
and
![]() .
As molar
mass
is
,
then
.
As molar
mass
is
,
then
![]() ,
and therefore this drop of water must
contain
,
and therefore this drop of water must
contain
![]() molecules.
molecules.
The
average volume of a water molecule must therefore be
![]() cm3,
and if we assume the molecules to be spherical the diameter of a
water molecule is about
cm3,
and if we assume the molecules to be spherical the diameter of a
water molecule is about
![]() cm
or
cm
or
![]() m,
a result confirmed by X-ray diffraction.
m,
a result confirmed by X-ray diffraction.
Example 1 A sample of 2 mg of polonium is found to emit 2.90 x 1018 alpha-particles during one half-life. If the relative atomic mass of polonium is 210, calculate a value for the Avogadro constant.
Solution During a half-life one half of the polonium atoms will have decayed. Therefore 2 mg of polonium would emit 5.80 x 1018 alpha-particles before it decayed completely.
Therefore
number
of moles in 2 mg
![]()
Therefore one mole contains
![]() particles
particles
a good approximation to the Avogadro constant.
A gas is a collection of a large number of molecules, which are in continuous rapid motion. The gas molecules have a size (molecular diameter) of the order of 10-10 m. Ordinarily, the distance between the gas molecules is of the order 10-9 m, i.e. about 10 times as large as their size. Therefore, the gas molecules can be considered as to be moving freely with respect to each other. However, during motion, when they come close to each other, they suffer a change in their velocities due to the inter-molecular forces. Therefore, such changes in velocities of the molecules of a gas are due to molecular collision.
Rudolf Claussius and James Clark Maxwell developed the kinetic theory of gases in order to explain gas laws in terms of the motion of the gas molecules. The theory is based on the following assumptions as regards to the motion (molecules and the nature of the gases:
Assumptions:
1. All gases consist of molecules. The molecules of a gas are all alike and differ from those of other gases.
The molecules of a gas are very small in size as compared to the distance between them.
The molecules of a gas behave as perfect elastic spheres.
The molecules are always in random motion. They have velocities in all directions ranging from zero to infinity.
During their random motion, the molecules collide against one another and the walls of the containing vessel. The collisions of the molecules with one another and with the walls of the vessel are perfectly elastic.
Between two collisions, a molecule moves along a straight line and the distance covered between two successive collisions is called the free path of the molecules.
The collisions are almost instantaneous i.e. the time during which a collision takes place is negligible as compared to the time taken by the molecule to cover the free path.
The molecules do not exert any force on each other except during collisions.
Equations of State
The conditions in which a particular material exists are described by physical quantities such as pressure, volume, temperature, and amount of substance. These variables describe the state of the material and are called state variables.
The
volume
![]() of
a substance is usually determined by its pressure
of
a substance is usually determined by its pressure
![]() ,
temperature
,
temperature
![]() ,
and
amount of substance, described by the mass
or number of moles
,
and
amount of substance, described by the mass
or number of moles
![]() .
Ordinarily, we can't change one
of these variables without causing a change in another. When the tank
of oxygen gets hotter, the pressure increases. If the tank gets too
hot, it explodes; this happens occasionally with overheated steam
boilers.
.
Ordinarily, we can't change one
of these variables without causing a change in another. When the tank
of oxygen gets hotter, the pressure increases. If the tank gets too
hot, it explodes; this happens occasionally with overheated steam
boilers.
The Ideal-Gas Equation
Experiments show that, at low enough densities, all real gases tend to obey the relation
![]() or
or
![]() (ideal-gas
equation)
(1)
(ideal-gas
equation)
(1)
where
![]() is
a proportionality constant. Equation
(1)
is
called the ideal
gas equation.
Provided the gas density is low, this law holds
for any single gas or for any mixture of different gases. (For a
mixture,
is
the
total number of moles in the mixture.) An ideal
gas
is
one for which Eq. (1) holds precisely for all
pressures
and temperatures. This is an idealized model; it works best at very
low pressures and high temperatures, when the gas molecules are far
apart and in rapid motion. It is reasonably good (within a few
percent) at moderate pressures (such as a few atmospheres) and at
temperatures well above those at which the gas liquefies.
is
a proportionality constant. Equation
(1)
is
called the ideal
gas equation.
Provided the gas density is low, this law holds
for any single gas or for any mixture of different gases. (For a
mixture,
is
the
total number of moles in the mixture.) An ideal
gas
is
one for which Eq. (1) holds precisely for all
pressures
and temperatures. This is an idealized model; it works best at very
low pressures and high temperatures, when the gas molecules are far
apart and in rapid motion. It is reasonably good (within a few
percent) at moderate pressures (such as a few atmospheres) and at
temperatures well above those at which the gas liquefies.
The numerical value of depends on the units of , , and . In SI units, in which the unit of is Pa (l Pa = l N/m2) and the unit of is m3, the current best numerical value of is
= 8.314472(15) j/mol • K
Note that the units of pressure times volume are the same as the units of work or energy (for example, N/m2 times m3); that's why has units of energy per mole per unit of absolute temperature.
We
can express the ideal-gas equation, Eq. (1),
in terms density
![]() of the gas,
using
of the gas,
using
![]() :
:
![]() .
.
From this we can get an expression for the density of the gas:
![]() (2)
(2)
For
a constant
mass (or
constant number of moles) of an ideal gas the product
![]() is
constant, so the quantity pV/T
is
also constant. If the subscripts 1 and 2 refer to any two states of
the same mass of a gas, then
is
constant, so the quantity pV/T
is
also constant. If the subscripts 1 and 2 refer to any two states of
the same mass of a gas, then
![]() .
.
Van der Waals Equation
The ideal gas equation can be obtained from a simple molecular model that ignores the volumes of the molecules themselves and the attractive forces between them.
 Meanwhile,
for real gases there is another equation of state, the van
der Waals equation,
that
makes approximate corrections for these two omissions. This equation
was developed by the 19th-century Dutch physicist J. D. van der
Waals; the
interaction between atoms was named the van
der Waals interaction after
him. The van der Waals equation is:
Meanwhile,
for real gases there is another equation of state, the van
der Waals equation,
that
makes approximate corrections for these two omissions. This equation
was developed by the 19th-century Dutch physicist J. D. van der
Waals; the
interaction between atoms was named the van
der Waals interaction after
him. The van der Waals equation is:
![]() (3)
(3)
The
constants
![]() and
and
![]() are
empirical constants, different for different gases. Roughly
speaking,
represents
the volume of a mole of molecules; the total volume
of the molecules is then
are
empirical constants, different for different gases. Roughly
speaking,
represents
the volume of a mole of molecules; the total volume
of the molecules is then
![]() ,
and
the net volume available for the molecules to
move around in is
,
and
the net volume available for the molecules to
move around in is
![]() .
The
constant
depends
on the attractive intermolecular
forces, which reduce the pressure of the gas for given values of
,
,
and
by
pulling
the
molecules together as they push
on
the walls of the container. The decrease
in pressure is proportional to the number of molecules per unit
volume in a layer near the wall (which are exerting the pressure on
the wall) and is also proportional to the number of molecules per
unit volume in the next layer beyond the wall (which
are doing the attracting). Hence the decrease in pressure due to
intermolecular
forces is proportional to
.
The
constant
depends
on the attractive intermolecular
forces, which reduce the pressure of the gas for given values of
,
,
and
by
pulling
the
molecules together as they push
on
the walls of the container. The decrease
in pressure is proportional to the number of molecules per unit
volume in a layer near the wall (which are exerting the pressure on
the wall) and is also proportional to the number of molecules per
unit volume in the next layer beyond the wall (which
are doing the attracting). Hence the decrease in pressure due to
intermolecular
forces is proportional to
![]() .
.
When
![]() is
small (that is, when the gas is dilute),
the
average distance between
molecules is large, the corrections in the van der Waals equation
become insignificant, and Eq. (3) reduces to the ideal-gas equation.
is
small (that is, when the gas is dilute),
the
average distance between
molecules is large, the corrections in the van der Waals equation
become insignificant, and Eq. (3) reduces to the ideal-gas equation.
Dalton's Law of Partial Pressures
If two or more gases are mixed in a container then the final pressure can be found from Dalton's law, which states that:
The pressure in a container is the sum of the partial pressures of the gases that occupy the container.
The
partial
pressure
of
a gas is that pressure that the gas would exert if it alone occupied
the container. For example, consider a container with a volume
and a temperature
.
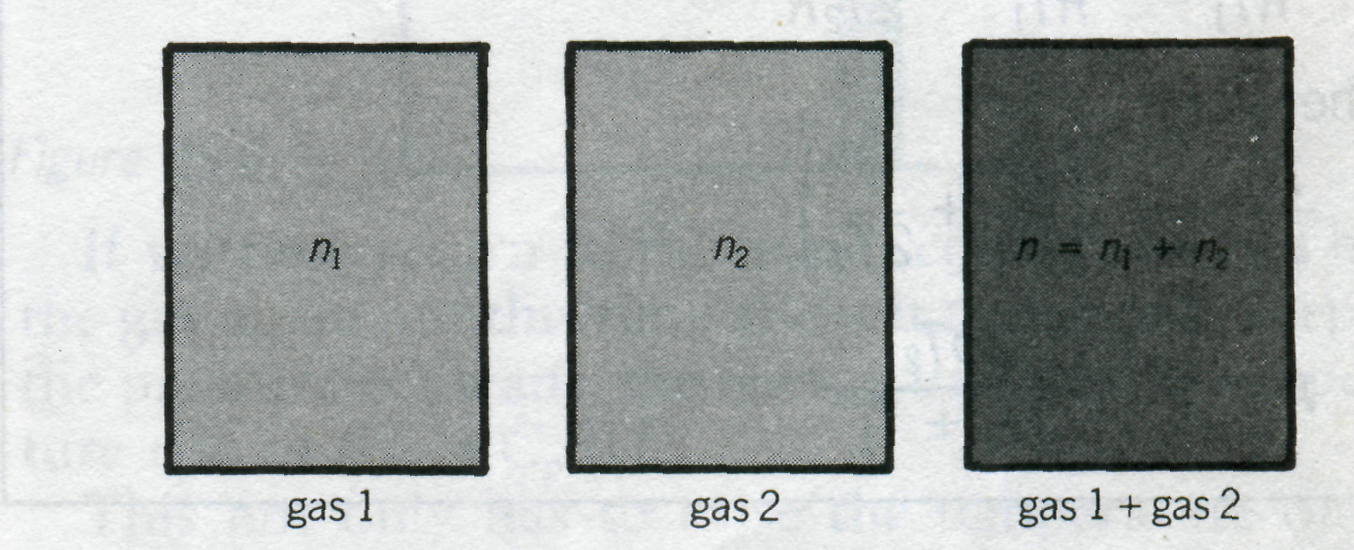
Let the container be occupied by two different gases, there being
![]() \
moles
of gas 1 and
\
moles
of gas 1 and
![]() moles
of gas 2 (Fig. 2). Let the partial pressures of the gases be
moles
of gas 2 (Fig. 2). Let the partial pressures of the gases be
![]() and
and
![]() .
.
|
Now
![]() and
and
![]() .
But
the total pressure in the container is
,
where
for
.
But
the total pressure in the container is
,
where
for
![]() ,
the
total number of moles of whatever type occupying the container.
Therefore
,
the
total number of moles of whatever type occupying the container.
Therefore
![]() ;
;
![]() and
and
![]() ,
,
and since , we have
![]() or
or
![]()
which is Dalton's law.
A useful application of this law is in cases where volumes of the same gas occupy separate but connected containers at differing temperatures.
Pressure Exerted by a Gas
A gas exerts pressure on the walls of the containing vessel due to continuous collisions of the molecules against the wall. During collisions the molecules exert forces on the walls of the container; this is the origin of the pressure the gas exerts.
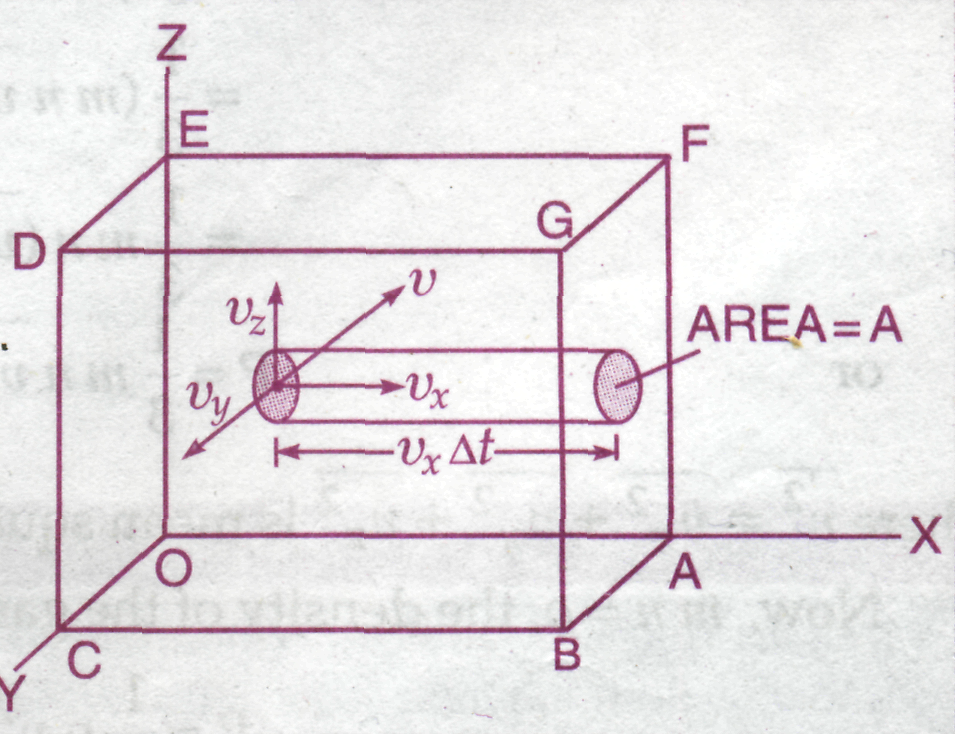
Consider
a gas contained in a vessel. Suppose that the edges OA, OC and OE of
the vessel are along X, Y and Z-axis respectively [Fig.3]. Let n
be
the number of the gas molecules per unit volume inside the vessel and
be
the mass of each molecule. Let
![]() be
the velocity of any gas molecule at any instant. If
be
the velocity of any gas molecule at any instant. If
![]() ,
,
![]() ,
,
![]() components of the velocity
along
components of the velocity
along
![]() ,
,
![]() and
and
![]() -axis
respectively, then
-axis
respectively, then
![]() .
.
The
molecule moves with momentum
![]() along
X-axis and strikes against the face ABGF. Since the collision is
perfectly elastic in nature, the molecule rebounds back with same
speed
.
As
the direction of motion is reversed, the momentum of the molecule
after the rebound becomes
along
X-axis and strikes against the face ABGF. Since the collision is
perfectly elastic in nature, the molecule rebounds back with same
speed
.
As
the direction of motion is reversed, the momentum of the molecule
after the rebound becomes
![]() .
Therefore,
change in momentum of the molecule along
-axis
.
Therefore,
change in momentum of the molecule along
-axis
![]()
Let
us find the change in momentum of the gas molecules hitting the area
![]() of the face ABGF in time
of the face ABGF in time
![]() .
Now,
in time
,
all
those molecules will hit the area
of the face ABGF, which lie in a cylinder of length
.
Now,
in time
,
all
those molecules will hit the area
of the face ABGF, which lie in a cylinder of length
![]() and
area of cross-section
.
and
area of cross-section
.
|
Therefore,
such molecules lie in volume
![]() .
Since
the number of molecules per unit volume is n,
the
number of such molecules is
.
Since
the number of molecules per unit volume is n,
the
number of such molecules is
![]() .
In
fact, on the average,
half of this number is expected to move along negative
-axis
and the other half
towards the face ABGF along positive
-axis.
Therefore, the number of molecules hitting the area
in time
along
positive
-axis
.
In
fact, on the average,
half of this number is expected to move along negative
-axis
and the other half
towards the face ABGF along positive
-axis.
Therefore, the number of molecules hitting the area
in time
along
positive
-axis
![]() .
.
Therefore, the total change in momentum of molecules in time along -axis,
![]() .
.
Now,
different molecules or even the same molecule at different times may
possess
different velocities. Therefore, in the above expression for
![]() ,
it
is reasonable to
replace
,
it
is reasonable to
replace
![]() by
by
![]() ,
where
is
mean square component of the velocities of the molecules along
-axis,
Therefore, in the above equation, replacing
by
,
we have
,
where
is
mean square component of the velocities of the molecules along
-axis,
Therefore, in the above equation, replacing
by
,
we have
![]() .
.
Now,
the rate of change of momentum is called force (Second Newton’s
law,
![]() ).
Therefore, force exerted by
walls of the vessel on the gas molecules along
-axis
is given by
).
Therefore, force exerted by
walls of the vessel on the gas molecules along
-axis
is given by
![]() .
.
According
to Newton's third law of motion, the gas molecules also exert an
equal but opposite force on the walls of the vessel. Therefore, force
![]() exerted by the gas molecules on the walls of container along
-axis,
exerted by the gas molecules on the walls of container along
-axis,
![]()
![]()
If
![]() is pressure exerted by gas molecules along
-axis,
then
is pressure exerted by gas molecules along
-axis,
then
![]() .
.
If
![]() and
and
![]() are pressures along
-axis
and
-axis
respectively, then
are pressures along
-axis
and
-axis
respectively, then
![]() and
and
![]() .
.
Since gas molecules have same properties in all directions, the choice of -axis, -axis and -axis is arbitrary. In other words, pressure exerted by the gas molecules must be same in all directions i.e.
![]() (say)
(say)
In other words,
![]() ,
or
,
or
![]() .
.
Or
![]() ,
(4)
,
(4)
where
![]() is
mean
square velocity of the gas molecules.
is
mean
square velocity of the gas molecules.
Now,
![]() ,
the
density of the gas. Therefore,
,
the
density of the gas. Therefore,
![]() .
(5)
.
(5)
The expression for the pressure exerted by a gas can be put in many other useful forms. From the equation (4), we have
![]()
Now,
![]() = average
kinetic energy of a gas molecule,
= average
kinetic energy of a gas molecule,
![]() ;
;
![]() .
.
If
is total number of gas molecules in volume
,
then
![]() .
Therefore, equation (4) becomes
.
Therefore, equation (4) becomes
![]() or
or
![]() (6)
(6)
Also, the equation (5) may be written as
![]() .
.
Now,
![]() =
average
kinetic energy of the gas per unit volume. And, Finally,
=
average
kinetic energy of the gas per unit volume. And, Finally,
![]() .
(7)
.
(7)
The assumption that individual molecules undergo perfectly elastic collisions with the container wall is actually a little too simple. More detailed investigation has shown that in most cases, molecules actually adhere to the wall for a short time and then leave again with speeds that are characteristic of the temperature of the wall. However, the gas and the wall are ordinarily in thermal equilibrium and have the same temperature. So there is no net energy transfer between gas and wall, and this discovery does not alter the validity of our conclusions.
Kinetic Energy of a Molecule and of One Mole of a Gas
Consider one mole of a monatomic gas. If , and are the pressure, volume and temperature, respectively, of the gas, then according to the ideal gas equation,
![]() ..
(8)
..
(8)
Let
be molar mass of the gas. Then, density of the gas is
![]() .
In the equation (5), substituting for
,
we have
.
In the equation (5), substituting for
,
we have
![]() or
or
![]() . (9)
. (9)
From the equations (8) and (9), we have
![]() . (10)
. (10)
Therefore, average kinetic energy of one mole of the gas,
![]() .
.
The
equation
(10)
gives mean
kinetic energy of one mole of the gas. Now,
one mole of the gas contains molecules equal to Avogadro number. If
![]() is
mass of one molecule and
is
mass of one molecule and
![]() ,
the Avogadro number, then
,
the Avogadro number, then
![]()
Therefore, the equation (10) becomes
![]()
Therefore, average kinetic energy of one molecule,
![]() ,
,
Now,
![]() is equal to the universal gas constant per molecule of the gas and
called Boltzmann's
constant. It
is denoted by
is equal to the universal gas constant per molecule of the gas and
called Boltzmann's
constant. It
is denoted by
![]() and
its value is J/(molecule x K). Therefore, the above equation may be
written as
and
its value is J/(molecule x K). Therefore, the above equation may be
written as
![]() (11)
(11)
The equation (11) gives average kinetic energy per molecule of the gas and it may be noted that it does not depend upon the mass of the molecule of the gas.
Relation between pressure and temperature of a gas
Let’s
return to perfect gas equation:
![]() .
The molar mass
can be expressed as product of mass of one molecular
.
The molar mass
can be expressed as product of mass of one molecular
![]() and
number of molecules in one mole, that is Avogadro number
:
and
number of molecules in one mole, that is Avogadro number
:
![]() /
Then
/
Then
![]() .
But
.
But
![]() ,
hence
,
hence
![]() .
The ratio of total mass
and mass of one molecular
gives the total
number
of molecules in given volume:
.
The ratio of total mass
and mass of one molecular
gives the total
number
of molecules in given volume:
![]() and
and
![]() .
Then, if we divide the total number
of molecules in given volume
by this volume, we obtain the number of molecules per unit volume,
that is, number
density
of molecules in given volume
.
Then, if we divide the total number
of molecules in given volume
by this volume, we obtain the number of molecules per unit volume,
that is, number
density
of molecules in given volume
![]() .
And, finally, we obtain very important result: pressure of gas
depends on temperature as
.
And, finally, we obtain very important result: pressure of gas
depends on temperature as
![]() . (12)
. (12)
Degrees of freedom
So
far we have only been considering monatomic gases. We must now extend
the ideas to cover gases of
higher atomicity, that is, molecules with more than one
atom per molecule. As we know, kinetic energy of one monatomic
molecule =
![]() .
We have considered the motion of these molecules to be in three
directions; we say that the molecule has three degrees of
freedom,
.
We have considered the motion of these molecules to be in three
directions; we say that the molecule has three degrees of
freedom,
![]() .
It
is
therefore sensible to suppose
that one-third of the total energy is associated with
each degree of freedom, and this is known as Boltzmann's
law
of equipartition of energy. Thus
each degree
of freedom has an amount of energy
.
It
is
therefore sensible to suppose
that one-third of the total energy is associated with
each degree of freedom, and this is known as Boltzmann's
law
of equipartition of energy. Thus
each degree
of freedom has an amount of energy
![]() associated with it.
associated with it.
Now consider a diatomic molecule. In addition to three translational degrees of freedom it can also rotate about three axes , and (Figure 7).
Figure 7 |
The
energy associated with axis
is very small, however, and so we say that the molecule has five
degrees of freedom,
![]() .
If we assume that the energy associated with each rotational degree
of freedom is the same as that for each translational degree of
freedom then the total energy of the molecule will be
.
If we assume that the energy associated with each rotational degree
of freedom is the same as that for each translational degree of
freedom then the total energy of the molecule will be
![]() .
.
(The vibrational energy of the molecule is insignificant except at very high temperatures.)
For
more complex molecules we have that
![]() (Three translational and three rotational)
(Three translational and three rotational)
Root-mean-square speed
From
Eq. (11)
we can obtain expressions for the square root of
![]() called
the root-mean-square
speed
(or
rms
speed)
called
the root-mean-square
speed
(or
rms
speed)
![]()
![]() (13)
(13)
It might seem more natural to characterize molecular speeds by their average value rather than by , but we see that follows more directly from Eqs. (11). To compute the rms speed, we square each molecular speed, add, divide by the number of molecules, and take the square root; vrms is the root of the mean of the squares.
Equations (11) shows that at a given temperature T, gas molecules of different mass m have the same average kinetic energy but different root-mean-square speeds. On average, the nitrogen molecules (M = 28 g/mol) in the air around you are moving faster than are the oxygen molecules (M = 32 g/mol). Hydrogen molecules (M = 2 g/mol) are fastest of all; this is why there is hardly any hydrogen in the earth's atmosphere, despite its being the most common element in the universe. A sizable fraction of any H2 molecules in the atmosphere would have speeds greater than the earth's escape speed of 1.12 x 104 m/s and would escape into space. The heavier, slower-moving gases cannot escape so easily, which is why they predominate in our atmosphere.
The Distribution of Molecular Speeds
Thus far we have neglected the fact that not all molecules in a gas have the same speed and energy. In reality, their motion is extremely chaotic. Any individual molecule is colliding with others at an enormous rate - typically, a billion times per second. Each collision results in a change in the speed and direction of motion of each of the participant molecules. From Equation 21.7, we see that average molecular speeds increase with increasing temperature. What we would like to know now is the relative number of molecules that possess some characteristic, such as a certain percentage of the total energy or speed. The ratio of the number that have the desired characteristic to the total number of molecules is the probability that a particular molecule has that characteristic.
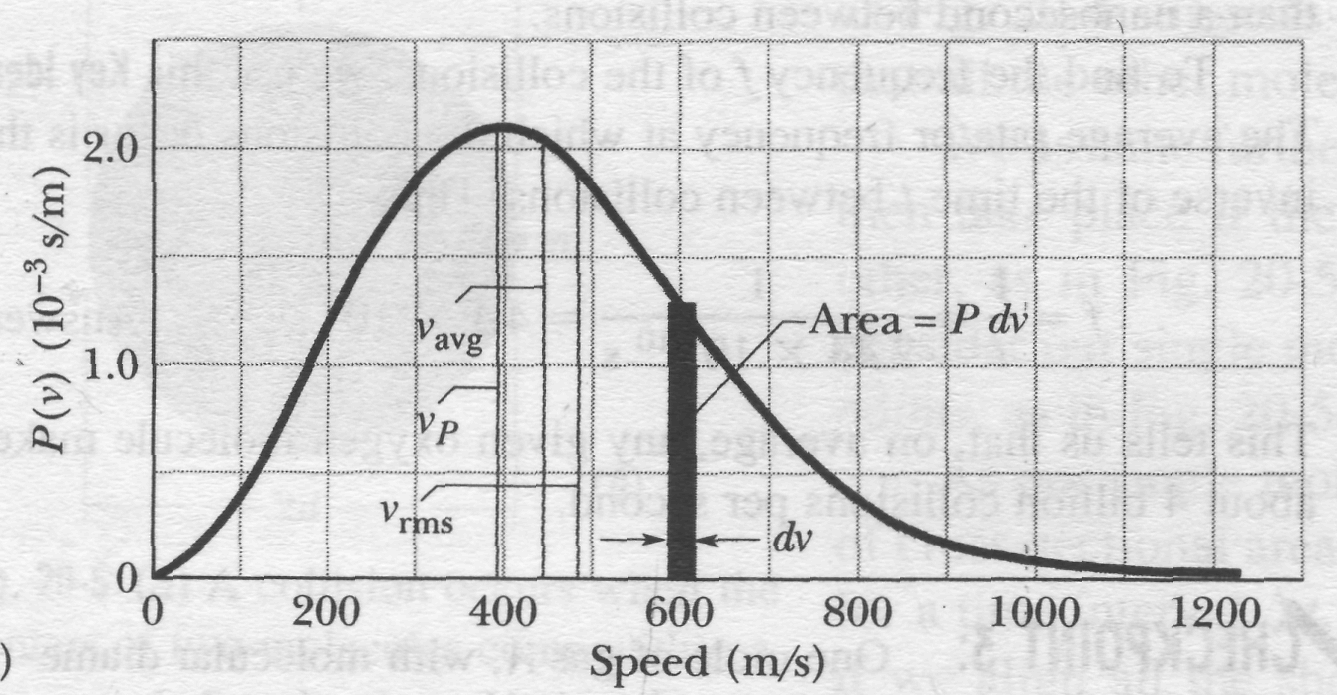
The root-mean-square speed gives us a general idea of molecular speeds in a gas at a given temperature. We often want to know more. For example, what fraction of the molecules have speeds greater than the rms value? Greater than twice the rms value? To answer such questions, we need to know how the possible values of speed are distributed among the molecules. Figure 4a shows this distribution for oxygen molecules at room temperature (T = 300 K); Fig.4b compares it with the distribution at T = 80 K.
In 1852, Scottish physicist James Clerk Maxwell first solved the problem of finding the speed distribution of gas molecules. His result, known as Maxwell's speed distribution law, is
![]() (14)
(14)
Here
is the molecular speed, T
is
the gas temperature, M
is
the molar mass of the gas, and R
is
the gas constant. It is this equation that is plotted in Fig. 4-a,b.
The
quantity P(v)
in
Eq. 14 and Fig. 4 is a
probability distribution function: For
any speed
,
the product
![]() (a
dimensionless quantity) is the fraction of molecules whose speeds lie
in the interval of width
(a
dimensionless quantity) is the fraction of molecules whose speeds lie
in the interval of width
![]() centered
on speed
.
centered
on speed
.
As
Fig. 4a shows, this fraction is equal to the area of a strip with
height
![]() and width
.
The
total area under the distribution curve corresponds to the fraction
of the molecules whose speeds lie between zero and infinity. All
molecules fall into this category, so the value of this total area is
unity; that is,
and width
.
The
total area under the distribution curve corresponds to the fraction
of the molecules whose speeds lie between zero and infinity. All
molecules fall into this category, so the value of this total area is
unity; that is,
![]()
|
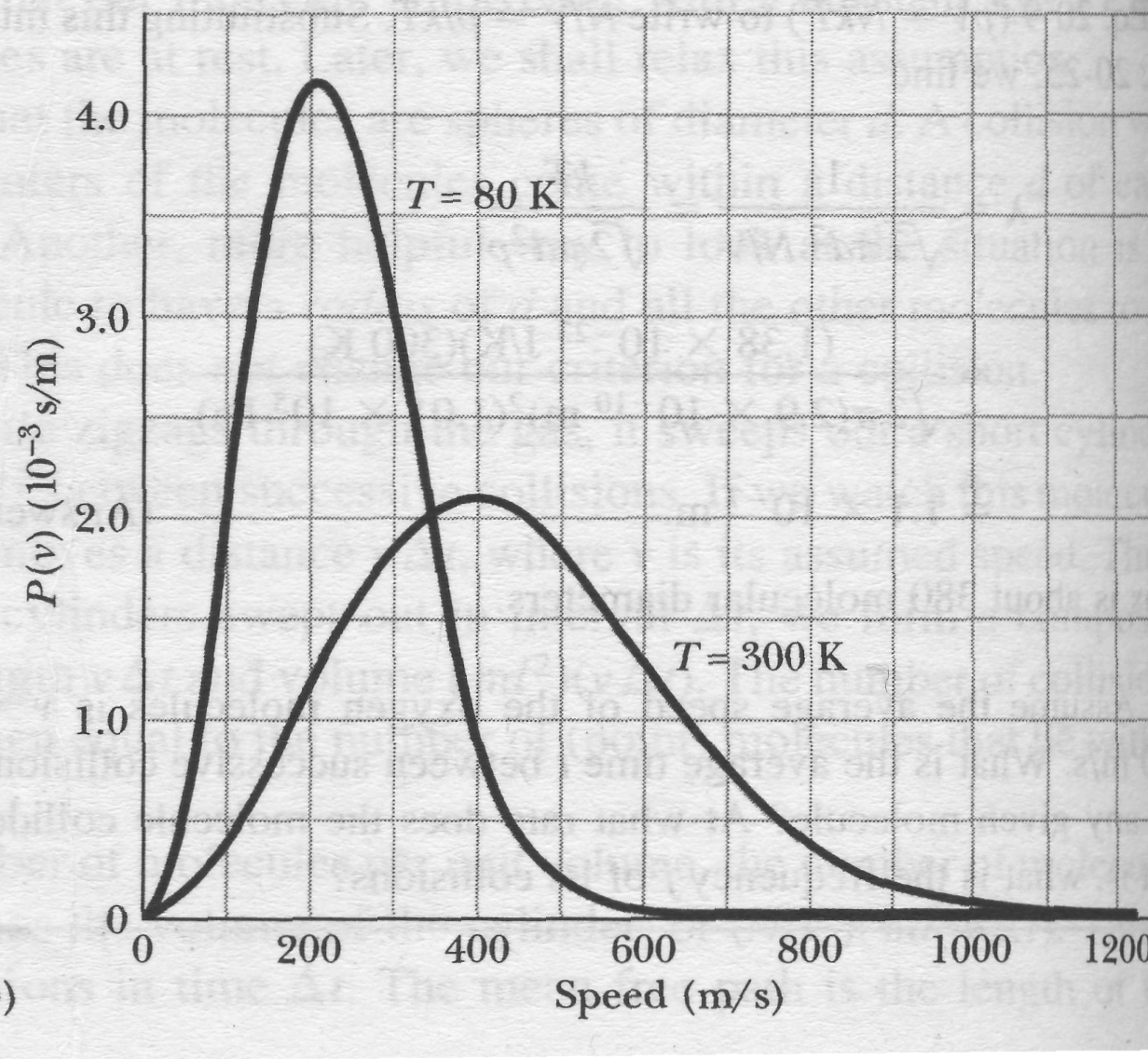
Fig. 4 (a) The Maxwell speed distribution for oxygen molecules at T = 300 K. The three characteristic speeds are marked, (b) The curves for 300 K and 80 K. Note that the molecules move more slowly at the lower temperature. Because these are probability distributions, the area under each curve has a numerical value of unity.
The
fraction (frac) of molecules with speeds in an interval of, say,
![]() ,
to
,
to
![]() is then
is then
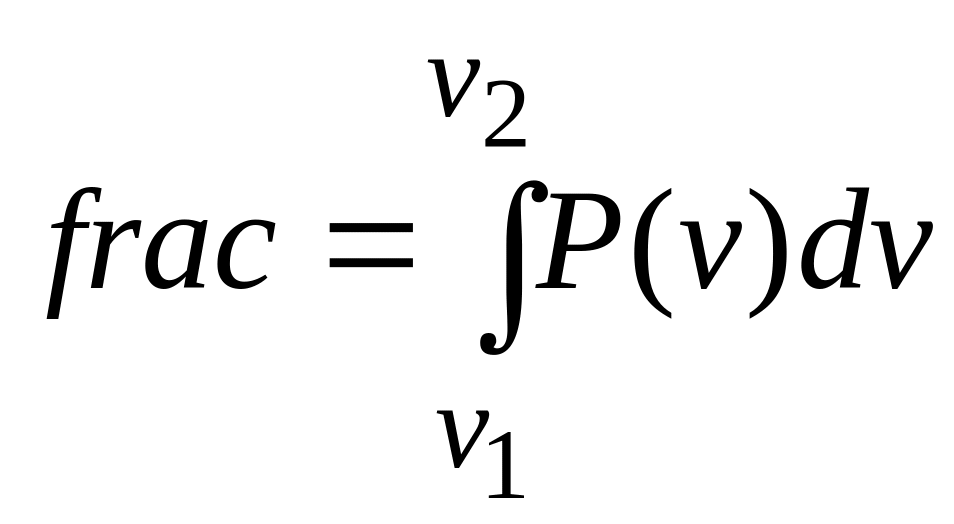
centered
on
.Then
we add up all these values of
![]() .
The
result is
.
The
result is![]() .
.
Average, RMS. and Most Probable Speeds
In
principle, we can find the average
speed
![]() of the molecules in a gas with the following procedure: We weight
each
value of
in the distribution; that is, we multiply it by the fraction
of molecules with speeds in a differential interval;
centered
on
.
Then we add up all these values of
of the molecules in a gas with the following procedure: We weight
each
value of
in the distribution; that is, we multiply it by the fraction
of molecules with speeds in a differential interval;
centered
on
.
Then we add up all these values of
![]() .The
result is
.
In practice, we do all this by evaluating
.The
result is
.
In practice, we do all this by evaluating
![]() (15)
(15)
Substituting for from Eq. 14 and using integral from the list o integrals, we find
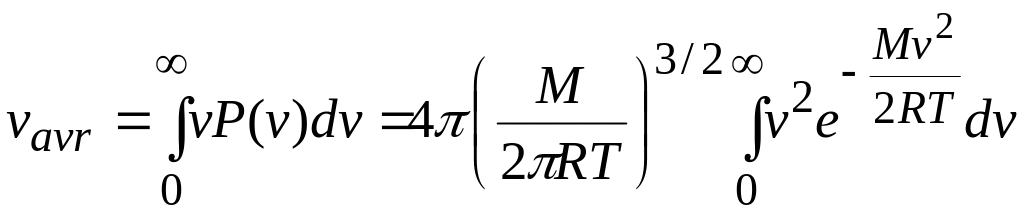 ,
,
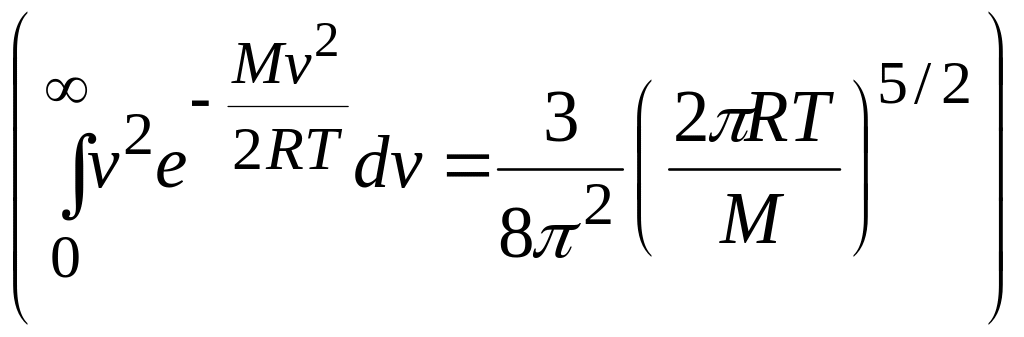 ,
Hence
,
Hence
![]() (average
speed). (16)
(average
speed). (16)
Similarly,
we can find the average of the square of the speeds
![]() with
with
![]() (17)
(17)
Substituting for from Eq. 14 and using generic integral from the list of integrals, we find
![]() .
.
The square root of is the root-mean-square speed vms. Thus,
(18)
which agrees with Eq. 12.
The
most
probable speed
![]() is
the speed at which
is maximum (see Fig. 4a). To calculate
,
we
set
is
the speed at which
is maximum (see Fig. 4a). To calculate
,
we
set
![]() (the slope of the curve in Fig 4
is
zero at the maximum of the curve) and then solve for
.
Doing so, we find
(the slope of the curve in Fig 4
is
zero at the maximum of the curve) and then solve for
.
Doing so, we find
![]() (19)
(19)
A molecule is more likely to have speed than any other speed, but some molecules will have speeds that are many times . These molecules lie in the high-speed tail of a distribution curve like that in Fig. 4. We should be thankful for these few, higher speed molecules because they make possible both rain and sunshine (without which we could not exist). We next see why.
Rain: The speed distribution of water molecules in, say, a pond at summertime temperatures can be represented by a curve similar to that of Fig. 4a. Most of the molecules do not have nearly enough kinetic energy to escape from the water through its surface. However, small numbers of very fast molecules with speeds far out in the tail of the curve can do so. It is these water molecules that evaporate, making clouds and rains a possibility.
As the fast water molecules leave the surface, carrying energy with them, the temperature of the remaining water is maintained by heat transfer from the surroundings. Other fast molecules - produced in particularly favorable collisions-quickly take the place of those that have left, and the speed distribution is maintained.
Sunshine: Let the distribution curve now refer to protons in the core of the Sun. The Sun's energy is supplied by a nuclear fusion process that starts with the merging of two protons. However, protons repel each other because of their electrical charges, and protons of average speed do not have enough kinetic energy to overcome the repulsion and get close enough to merge. Very fast protons with speeds in the tail of the distribution curve can do so, however, and for that reason the Sun can shine.
Collisions between Molecules, Mean Free Path
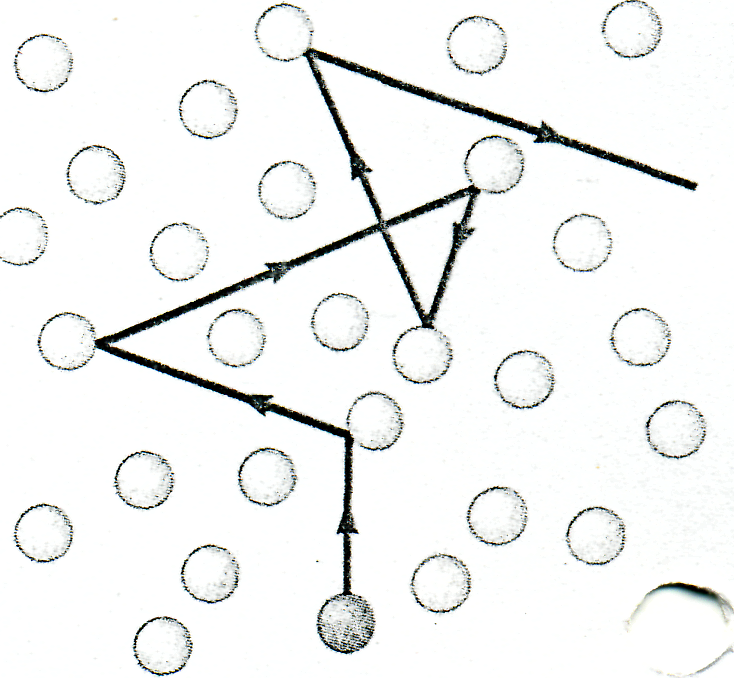
Most of us are familiar with the fact that the strong odor associated with a gas such as ammonia may take a fraction of a minute to diffuse throughout a room. However, because average molecular speeds are typically several hundred meters per second at room temperature, we might expect a diffusion time much less than 1 s. But, molecules collide with one other because they are not geometrical points. Therefore, they do not travel from one side of a room to the other in a straight line. Between collisions, the molecules move with constant speed along straight lines. The average distance between collisions is called the mean free path. The path of an individual molecule is random and resembles that shown in Figure 5. As we would expect from this description, the mean free path is related to the diameter of the molecules and the density of the gas.
Figure 5 |
Fig. 6 |
The
mean free path
![]() equals the average distance
traveled
in a time t
divided
by the number of collisions that occur in that time:
equals the average distance
traveled
in a time t
divided
by the number of collisions that occur in that time:
![]() (20)
(20)
Because
the number of collisions in a time
![]() is
,
the
number of collisions per unit time, or collision
frequency
is
,
the
number of collisions per unit time, or collision
frequency
![]() ,
is
,
is
![]() .
(21)
.
(21)
The
inverse of the collision frequency is the average time between
collisions, known as the mean
free time
![]() . (22)
. (22)
Our analysis has assumed that molecules in the cylinder are stationary. When the motion of these molecules is included in the calculation, the correct results are
![]() , (23)
, (23)
![]() . (24)
. (24)
The Boltzmann Distribution Law
The Exponential Atmosphere
We begin by considering the distribution of molecules in our atmosphere. Let us determine how the number of molecules per unit volume varies with altitude. Our model assumes that the atmosphere is at a constant temperature T. (This assumption is not entirely correct because the temperature of our atmosphere decreases by about 2°C for every 300-m increase in altitude. However, the model does illustrate the basic features of the distribution.)
According
to the ideal gas law, a gas containing N
molecules
in thermal equilibrium obeys the relationship
![]() .
It
is convenient to rewrite this equation in terms of the number
density
.
It
is convenient to rewrite this equation in terms of the number
density
![]() ,
which
represents the number of molecules per unit volume of gas. This
quantity is important because it can vary from one point to another.
In fact, our goal is to determine how
,
which
represents the number of molecules per unit volume of gas. This
quantity is important because it can vary from one point to another.
In fact, our goal is to determine how
![]() changes
in our atmosphere. We can express the ideal gas law in terms of
as
changes
in our atmosphere. We can express the ideal gas law in terms of
as
![]() .
Thus,
if the number density
is
known, we can find the pressure, and vice versa. The pressure in the
atmosphere decreases with increasing altitude because a given layer
of air must support the weight of all the atmosphere above it - that
is, the greater the altitude, the less the weight of the air above
that layer, and the lower the pressure. To determine the variation in
pressure with altitude, let us consider an atmospheric layer of
thickness dy
and
cross-sectional area
,
as shown in Figure 21.9. Because the air is in static equilibrium,
the magnitude PA
of
the upward force exerted on the bottom of this layer must exceed the
magnitude of the downward force on the top of the layer,
.
Thus,
if the number density
is
known, we can find the pressure, and vice versa. The pressure in the
atmosphere decreases with increasing altitude because a given layer
of air must support the weight of all the atmosphere above it - that
is, the greater the altitude, the less the weight of the air above
that layer, and the lower the pressure. To determine the variation in
pressure with altitude, let us consider an atmospheric layer of
thickness dy
and
cross-sectional area
,
as shown in Figure 21.9. Because the air is in static equilibrium,
the magnitude PA
of
the upward force exerted on the bottom of this layer must exceed the
magnitude of the downward force on the top of the layer,![]() ,
by
an amount equal to the weight of a gas molecule in the layer
,
by
an amount equal to the weight of a gas molecule in the layer
![]() ,
and
if a total number of N
molecules
are in the layer, then the weight of the layer is given by
,
and
if a total number of N
molecules
are in the layer, then the weight of the layer is given by
![]() .
Thus,
we see that
.
Thus,
we see that
![]()
This expression reduces to
![]()
Because
and T
is
assumed to remain constant, we
see
that
![]() .
Substituting
this result into the previous expression for dP
and
rearranging terms, we have
.
Substituting
this result into the previous expression for dP
and
rearranging terms, we have
![]()
Integrating this expression, we find that
![]() (25)
(25)
where
the constant
![]() is
the number density at y
=
0. This result is known as the Boltzmann
distribution law.
is
the number density at y
=
0. This result is known as the Boltzmann
distribution law.
According7 to Equation 21.23, the number density decreases exponentially with increasing altitude when the temperature is constant. The number density of our atmosphere at sea level is about n0 = 2.69 X 1025 molecules/m3. Because the pressure is , we see from Equation 21.23 that the pressure of our atmosphere varies with altitude according to the expression
![]() Law
of atmosphere
(26)
Law
of atmosphere
(26)