Решите самостоятельно.
Упростите выражение
.
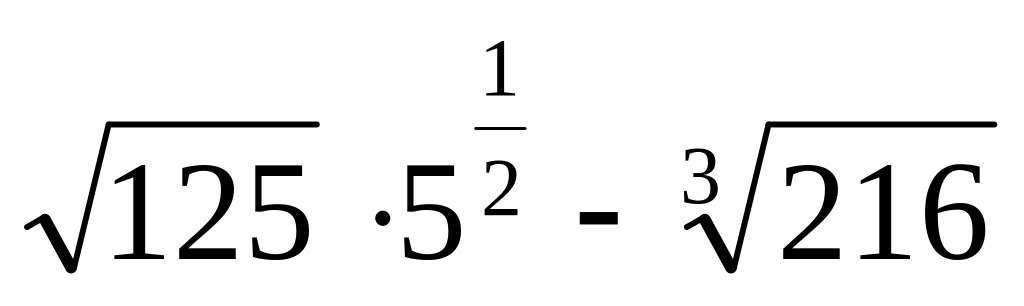1)
; 2)
; 3)19; 4)
.
2.Упростите выражение
.
1)
; 2)
; 3)
; 4)
;
3.Упростите выражение
.
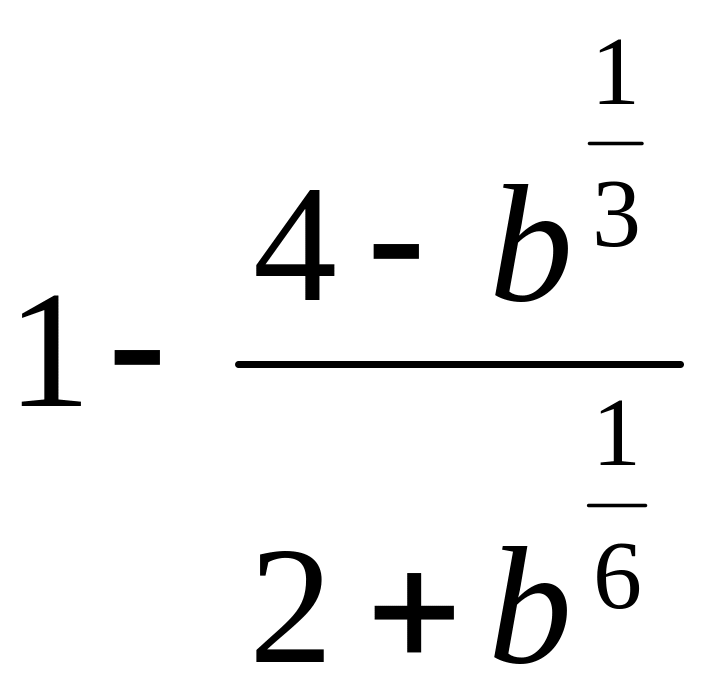1)
; 2)
; 3)
; 4)
.
4.Упростите выражение
.
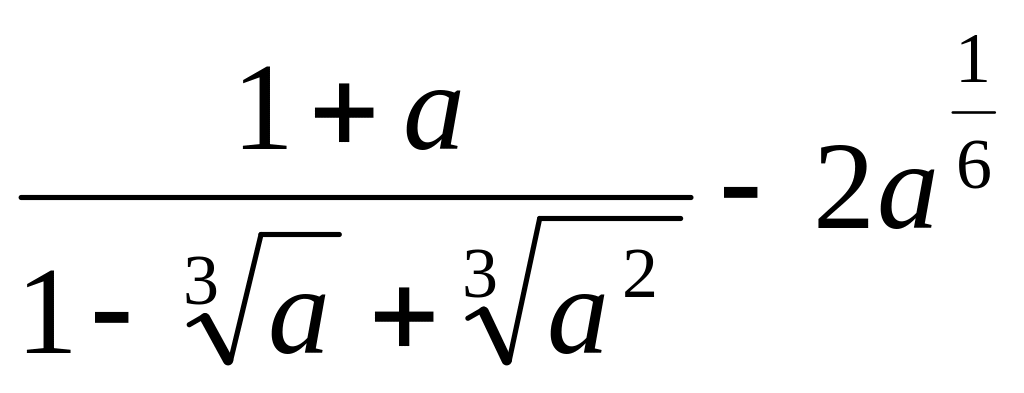1)
;
2)
; 3)
; 4)
.
5.Упростите выражение
.
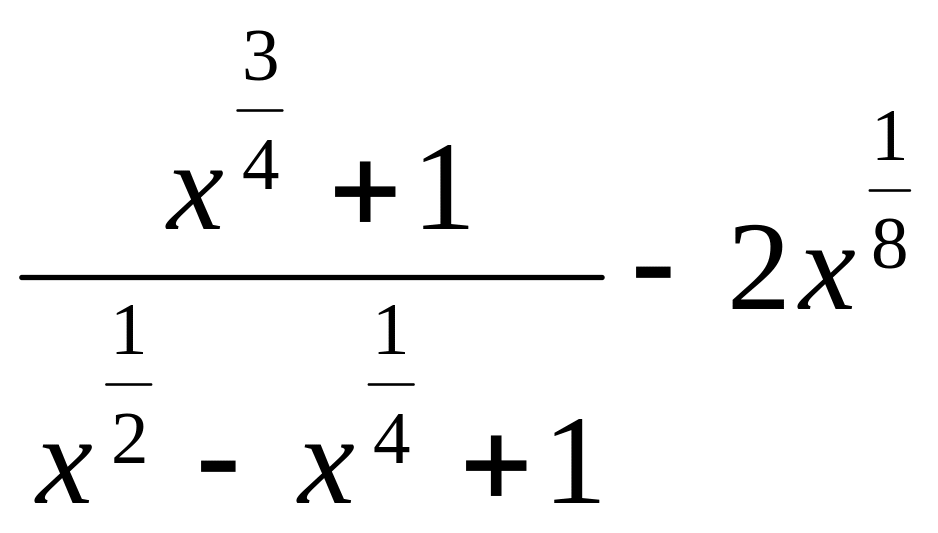1)
; 2)
; 3)
; 4)
.
5. Иррациональные уравнения.
Пример 1. Укажите промежуток, на
котором лежит корень уравнения
.
1)
; 2)
; 3)
; 4)
.
Решение. Возведем обе части
уравнения в квадрат:
.
После преобразований получим
.
Проверим, является ли –1 корнем исходного
уравнения:
,
.
Последнее равенство верно, следовательно,
-1 - искомый корень. Так как
,
то верный ответ №4.
О т в е т: 4.
Пример 2. Сколько корней имеет
уравнение
?
1) ни одного; 2) один; 3) два; 4)четыре;
Решение.
;
;
;
;
.
Проверка.
- равенство неверно, значит, 2 – не корень.
- равенство неверно, значит, -2 – не
корень.
О т в е т: 1.
Пример 3. Найдите решение системы
уравнений
и вычислите значение суммы
.
1) 7; 2) 5; 3) 3; 4) 2.
Решение. Введем обозначения:
.
Получим:
Умножим второе уравнение на 2 и сложим
с первым:
.
Отсюда получаем:
.
Подставив 2 в первое уравнение, получим:
.
Итак,
,
следовательно,
,
значит,
.
Итак, пара
- искомое решение системы уравнений:
.
О т в е т:2.
Решите самостоятельно.
Укажите промежуток, которому принадлежит корень уравнения
.
1) (-6;-3); 2) (-3;0); 3) (0;3); 4) (3;6).
Сколько корней имеет уравнение
?
1) четыре; 2) два; 3) один; 4) ни одного.
Найдите сумму корней уравнения
.
1) –1; 2) 1; 3) 4; 4) 5.
Найдите решение
системы уравнений
и вычислите значение суммы
.
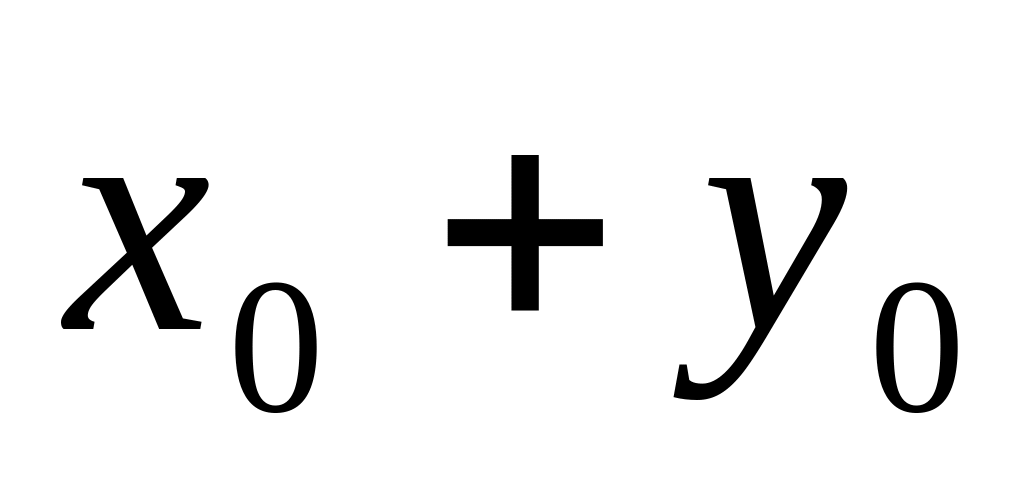1) 4; 2) 5; 3) 7; 4) 10.
6. Основные методы решения алгебраических уравнений.
Линейные уравнения
.
Такое уравнение имеет один корень,
нахождение которого не вызывает
затруднений:
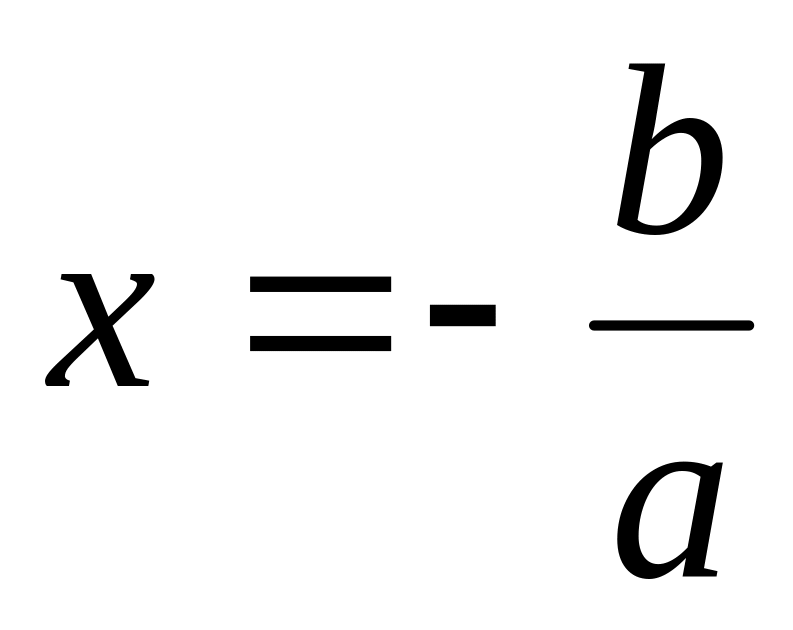.Квадратное уравнение
.
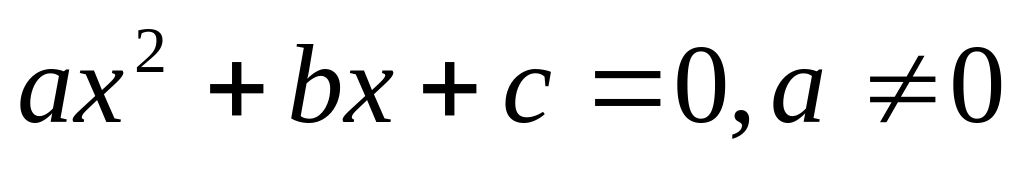Квадратные уравнения решаются по
готовой формуле
;
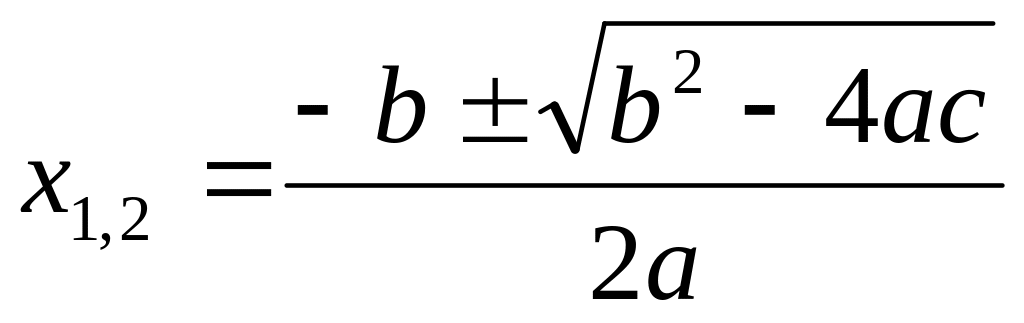используется теорема Виета:
.
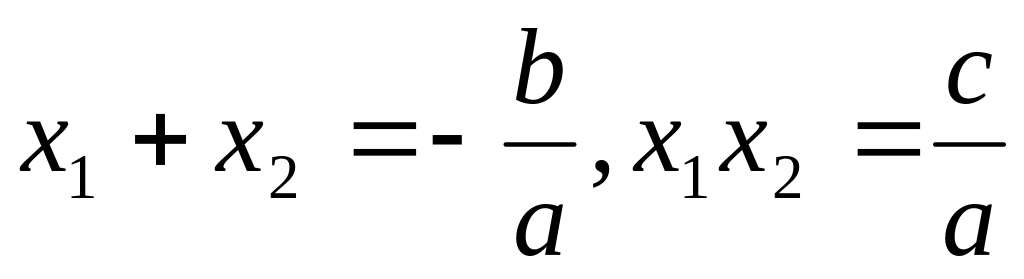Пример 1. Решить
уравнение
.
Решение.
Предложенное уравнение не является
алгебраическим. Более того, не любые
значения неизвестной
могут выступать в качестве корней этого
уравнения. Начинать решение таких
уравнений необходимо
с указания
области определения переменной
.
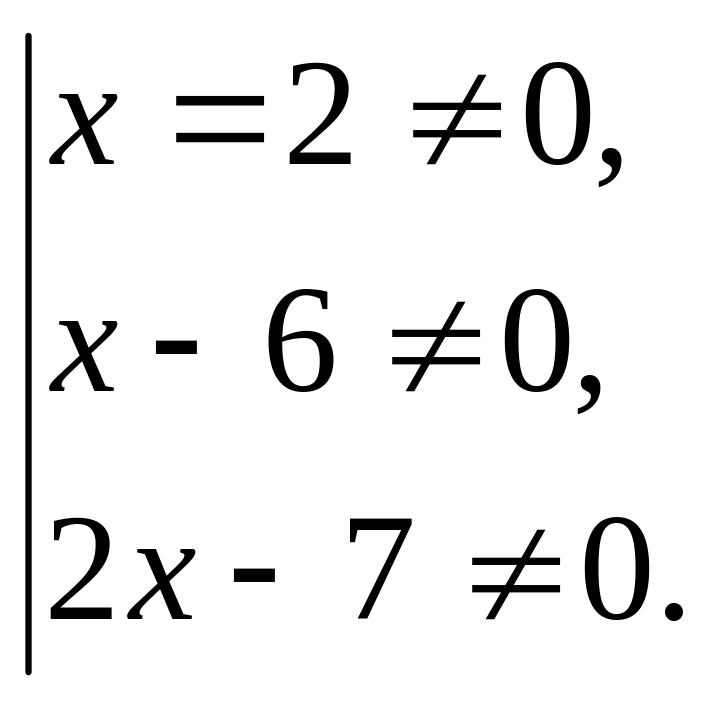(1)
Теперь приводим
уравнение к виду
и раскрываем скобки:
.
Приводим подобные слагаемые и получаем:
.
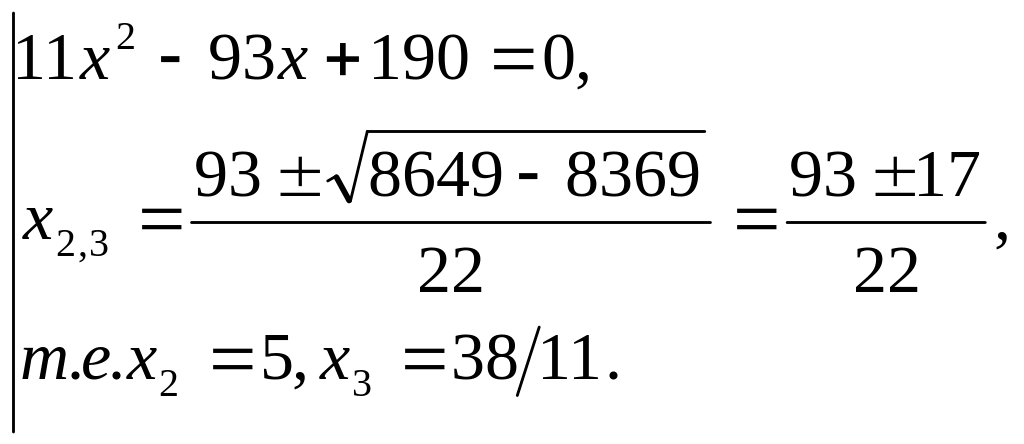
Найденные значения удовлетворяют соотношениям (1).
О т в е т:
З а д а ч и. Решить уравнения.
Уравнения степени большей чем 2.
А. Метод группировки. Путём группировки слагаемых, применения формул сокращенного умножения привести (если удается) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа – ноль. Затем приравниваем к нулю каждый из сомножителей.
Пример 2. Найти
корни уравнения
.
Решение:
,
группируем:
,
О т в е т:
Замечание: корни уравнения можно
было легко найти, пользуясь теоремой
Виета для кубического уравнения: если
,
то
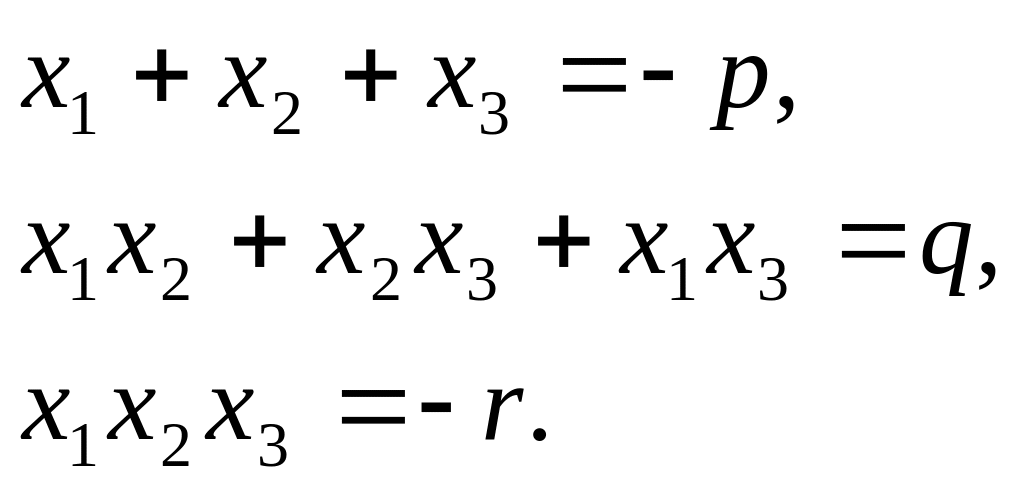
В нашем случае
З а д а ч и. Решить уравнения.
1)
2)
