3.2.4. Парето оптимальные решения

Для обсуждения того, как эта трудность может быть преодолена, рассмотрим следующий пример.

Пример 3-8 (разработка модели автомобиля). Предположим, что при разра­ботке модели автомобиля нас интересуют следующие два показателя: его срок службы (u) и его максимальная скорость (v), причем мы хотим максимизиро­вать оба эти показателя. В наших возможностях варьирование некоторых техни­ческих характеристик автомобиля (мощность двигателя, форма кузова, вес от­дельных агрегатов и т. п.) в некоторых заданных границах. При этом каждому фиксированному набору значений этих характеристик соответствует определенное значение u₀ срока службы автомобиля и значение v₀ его предельной скорости. Таким образом, взяв за альтернативы наборы значений варьируемых характери­стик автомобиля, а в качестве исходов соответствующие им пары чисел (u₀, v₀), приходим к задаче выбора решения в условиях определенности. Изобразив все такие пары чисел (u₀, v₀) на плоскости переменных u и v, получим (рис.3-6) не­которую область D, каждая точка которой представляет геометрически возмож­ный исход. Так как при принятии решения в условиях определенности выбор альтернативы равнозначен выбору исхода, то принятие решения состоит здесь в выборе конкретной точки области D. Какую точку надо взять в качестве оптимальной?

Пусть мы выбрали, например, точку M₀. Построим, как указано на рис.3.6, криволинейный треугольник АМ₀В. Для любой точки этого треугольника оба показателя — срок службы автомо­биля и его предельная скорость — будут большими, чем для точки M₀. Поэтому выбор любой точки этого треугольника будет более целесообразным, чем выбор точки M₀, а выбор точки M₀ в качестве оптимальной оказался неудачным. Аналогичное рассуждение при­менимо к любой точке области D, для которой возможно построе­ние указанного на рис.3.6 криволинейного треугольника.

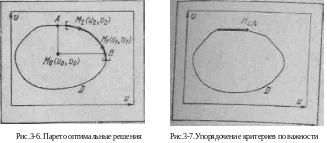
Итак, при выборе исхода надо ограничиться теми точками об­ласти D, для которых построение такого криволинейного треуголь­ника невозможно. В содержательных терминах это означает, что надо ограничиться теми исходами, для которых невозможно одновременное улучшение обоих показателей, такие исходы называются эффективными или оптимальными по Парето (По имени известного итальянского инженера, математика и экономиста Вильфредо Парето).

Формально условие эффективности точки (u, v)  D выражается так:

(u',v')  D, u'  u, v'  v  u'=u, v'=v.

Множество всех эффективных точек (на рис.3-6 оно указано жир­ной линией) представляет собой, образно говоря, северо-восточную границу области D. Таким образом, первый вывод, который можно сделать состоит в том, что выбор исхода следует производить из множества эффективных точек.

Однако какую именно эффективную точку следует признать в качестве оптимальной? Сравним две эффективные точки M1 (u₁, v₁) и М₂(u₂, v₂) (рис.3-6). Для точки M₁ больше первый по­казатель (срок службы), а для точки М₂ — второй (максимальная скорость). Для эффективных точек такая ситуация является типич­ной. Действительно, если для одной из точек области D оба пока­зателя являются большими, чем для другой (по крайней мере один показатель строго больше), то эта другая не будет эффективной, как это сразу следует из условия оптимальности. Итак, считая для двух то­чек области D лучшей ту, для которой все показатели лучше, по­лучаем, что для любых двух эффективных точек ни одна не явля­ется лучше другой. Иными словами, эффективные точки являются несравнимыми между собой по предпочтению, а если мы все же хотим как-то сравнить, сопоставить две эффективные точки, то для этого требуется дополнительная информация, кроме той, которая заключена в сравнении исходов по каждому показателю в отдель­ности. Точнее, для сравнения эффективных точек необходима до­полнительная информация следующего типа: сколькими единицами выигрыша по одному показателю можно компенсировать про­игрыш единицы по другому показателю? Такую информацию бу­дем в дальнейшем называть информацией о соотношении показа­телей эффективности. Рассмотрим два наиболее важных способа задания такой дополнительной инфор­мации и ее влияние на выбор опти­мального исхода (применительно к нашему примеру).

1. Упорядочение показателей по важности. Пусть нам известно, что один показатель существенно важнее другого, например, что максимальная скорость автомобиля существенно важ­ней его срока службы. В этом случае потерю единицы показателя v нельзя компенсировать никаким увеличением значения показателя u; значит, мы должны производить выбор оптимального исхода среди тех исходов, для которых значение показателя v является максималь­ным среди возможных, т. е. должны ограничиться исходами, изо­браженными на рис.3-7 жирной линией. У всех этих исходов значе­ние показателя v одинаково, поэтому наилучшим среди них будет тот, который имеет наибольшее значение показателя u; этот исход и выступает в качестве оптимального исхода M_opt.

2. Задание весов относительной важности. Должно быть извест­но, что один показатель в определенное число раз важнее другого, скажем, максимальная скорость автомобиля для нас в 2,5 раза важней его срока службы. Другими словами, потеря пяти единиц времени службы автомобиля приравнивается к приращению двух единиц его скорости. Важно отметить, что данное предположение о соотношении показателей должно относиться ко всем возможным моделям автомобилей, т. е. ко всем точкам области D, поэтому на плоскости переменных u и v мы можем отождествить любые две точки M1(u1,v1) и M2(u2,v2) области D, для которых

.

Геометрически это означает, что мы рассматриваем семейство прямых 2u+5v=const и считаем равноценными любые два исхода, принадлежащие одной прямой этого семейства (рис.3-8).

С другой стороны, пусть исходы М'(u', v') и М" (u", v") лежат на разных прямых этого семейства. Так как исход М* строго луч­ше исхода М' (для М* оба показателя лучше, чем для М') и, свою очередь, исход М* равноценен исходу М", то исход М" лучше, чем исход М'. Таким образом, для любых двух исходов лучшим следует признать тот, который расположен на более «вы­сокой» прямой семейства, а оптимальным — исход, соответствую­щий той точке M_opt области D, которая лежит на самой «высокой» прямой семейства.

Какие эффективные точки здесь выступают в качестве опти­мальных? Ясно, что положение оптимальной точки M_opt зависит от угла наклона прямых семейства, который, в свою очередь, опре­деляется отношением весов относительной важности показателей u и v (в нашем случае это отношение равно 2:5). При изменении отношения весов относительной важности показателей будет ме­няться наклон прямых семейства, а значит, и точка M_opt. Более того, любая эффективная точка может превратиться в точку M_opt, при подходящем отношении весов относительной важности — это достаточно ясно из геометрических представлений (рис.3-8).

П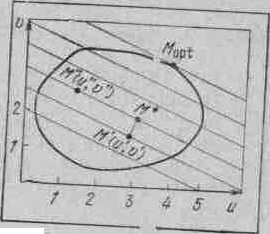 одводя итог обсуждения примера 3-8, можно сделать следую­щий общий вывод: если для многокритериальной задачи принятия решения мы не располагаем никакой дополнительной информа­цией о предпочтениях исходов, кроме той, которая обусловлена их сравнением по каждому показателю в отдельности, то мы можем говорить лишь о множестве оптимальных решений, в качестве ко­торого выступает множество всех эффективных точек. Выделение единственного оптимального решения в такой задаче можно произ­вести при наличии дополнительной информации о предпочтениях исходов в виде соотношения между показателями эффективности. Отметим, что для многокритериальной задачи, как правило, не существует исхода, наилучшего сразу по всем показателям, поэто­му оптимальное решение чаще всего является компромиссным.