
- •Тема 3. Принятие решений в условиях определенности
- •Тема 3. Принятие решений в условиях определенности 1
- •3.1. Однокритериальные задачи
- •3.2. Многокритериальные задачи принятия решений
- •3.2.1. Построение интегральных критериев
- •3.2.3. Комментарий е.С.Вентцель [1]
- •3.2.4. Парето оптимальные решения
- •3.3. Методы нахождения множества Парето
- •3.5.Обсуждение многокритериальности
- •3.6.Человекомашинные процедуры
- •3.6.1.Классификация чмп
- •3.6.2.Прямые человекомашинные процедуры
- •3.6.3.Процедуры оценки векторов
- •3.6.4.Процедуры поиска удовлетворительных значений критериев
- •3.6.5.Исследование решений на множестве Парето
- •Библиографический список
3.2. Многокритериальные задачи принятия решений
Так как для задач принятия решений в условиях определенности с численной оценкой исходов цель адекватна максимизации (или минимизации) целевой функции, то для таких задач имеется фактически единственная концепция оптимальности решения: оптимальным будет решение, доставляющее целевой функции наибольшее (или наименьшее) значение.
К сожалению, на практике такие задачи,
где единственный критерий однозначно
определяет цель, встречаются не часто,
даже при рассмотрении небольших и
скромных по масштабу мероприятий.
Например, имея цель приобрести персональный
компьютер, мы выбираем его исходя из
таких критериев как быстродействие,
объем оперативной памяти, габариты,
потребляемая мощность, стоимость и этим
список не ограничивается. Традиционное
понятие оптимальности, основанное на
нахождении экстремума одного критерия,
в условиях многокритериальности
теряет смысл: решение оптимальное по
одному критерию совсем не обязательно
будет оптимальным и по остальным. Поэтому
при наличии вектора критериев
![]() говорят
не об оптимальности по отдельным
критериям, а об оптимальности по
вектору критериев.
говорят
не об оптимальности по отдельным
критериям, а об оптимальности по
вектору критериев.
Какое решение будет здесь оптимальным? Ответить на этот вопрос гораздо сложнее, чем это может показаться с первого взгляда. Подчеркнем, что в данном случае речь идет не о том, как найти оптимальное решение, а о том, что следует понимать под оптимальным решением, т. е. мы сталкиваемся здесь с трудностью не технического, а, как говорят, иногда, концептуального характера.
3.2.1. Построение интегральных критериев
Построение интегрального критерия является радикальным средством преодоления трудностей решения многокритериальных задач, поскольку с его помощью, в идеале, адекватно моделируется система предпочтений ЛПР.
Метод основан на предположении о существовании функции F(u(x)) вектора критериев u(x)=(u1(x),…, uk(x)), такой что
F(u(x)) > F(u(y)) ( x y), x,yX.
Функция
F(u(x))
однозначно определяет
предпочтения ЛПР на множестве альтернатив
X.
Назовем
F(u(x))
интегральным критерием (в
отличие от частных критериев, являющимися
компонентами вектора u(x)).
Наличие интегрального критерия сводит
процедуру выбора решения по многим
критериям к однокритериальной задаче
математического программирования:
найти
![]() .
.
Первый вопрос, требующий своего решения при построении интегрального критерия, относится к виду функции F(u(x)). Прежде всего следует определить структуру связей частных критериев u1(x),…, uk(x) в интегральный критерий F(u(x)).
[Брук н]
1. Лексикографический метод. Простейшей такой структурой является лексикографическое упорядочение множества частных критериев. Оно основано на понятии абсолютной важности.
Определение. Критерий u1 абсолютно важнее критерия u2 если условие
![]()
выполняется при любых оценках альтернатив x и y по критерию u2.
Согласно данному определению, решение x предпочтительнее решения y , если оно имеет большее значение критерия u1 , независимо от того, хуже оно или лучше по критерию u2. Такой подход к определению предпочтений означает, что сколь угодно малый проигрыш в значении более важного критерия нельзя скомпенсировать сколь угодно большим выигрышем в значении менее важного критерия. В тех случаях, когда это условие выполняется с достаточной точностью, лексикографический подход позволяет находить оптимальные решения.
Определение. Критерии u1,…, uk лексикографически упорядочены, если для любого i>j критерий ui абсолютно важнее критерия uj.
Лексикографическое упорядочение критериев диктует следующий алгоритм поиска оптимального решения на множестве сравниваемых альтернатив X.
1. Решается задача математического программирования:
найти
![]()
Если значению
![]() соответствует единственное решение
соответствует единственное решение![]() ,
то оно является оптимальным. В противном
случае переходим к следующему шагу.
,
то оно является оптимальным. В противном
случае переходим к следующему шагу.
2. Решается задача математического программирования:
найти
![]()
при ограничениях
![]() .
.
Если данная задача имеет единственное решение , то оно является оптимальным. В противном случае переходим к следующему шагу.
3. В конце концов, на t-м шаге, решая задачу:
найти
![]()
при ограничениях
![]()
получим единственное решение , которое выберем в качестве оптимального.
Отметим, что остальные k-t критериев не использовались и, следовательно, оценки сравниваемых альтернатив по этим критериям не повлияли на выбор.
Примеры, иллюстрирующие лексикографический метод решения многокритериальных задач, приведены на рис.3-3.
Если критерий u1 имеет единственную экстремальную точку (рис.3-3, а), то она будет соответствовать оптимальному решению. Это решение оказывается найденным уже на первом шаге. Критерий u2 при этом не используется.
Д
Рис.3-3. Иллюстрации
лексикографического метода, при котором
решение находится: а) на первом этапе;
б) на втором этапе

![]() ,
содержащее больше одного решения.
Поэтому оптимальное решение
находится только на втором шаге, когда
вводится в рассмотрение критерий u2
и определяется
,
содержащее больше одного решения.
Поэтому оптимальное решение
находится только на втором шаге, когда
вводится в рассмотрение критерий u2
и определяется
![]() .
.
Стремление ослабить требования, накладываемые лексикографическим методом на систему предпочтений ЛПР, привело к разработке его модификации - лексикографического метода с уступками. Этот метод в ограниченных пределах допускает компенсацию уменьшения значения более важного критерия за счет увеличения значений менее важных.
На первом шаге задача решается так же
как и раньше. На втором шаге максимизируется
значение критерия u2,
но уже при условии, что
![]() ,
где δ1
-назначаемая уступка по критерию u1.
На третьем шаге максимизируется
значение u3
при условии, что
,
,
где δ1
-назначаемая уступка по критерию u1.
На третьем шаге максимизируется
значение u3
при условии, что
,
![]() ,
т.е. первые два критерия отличаются
от своих оптимальных значений не больше,
чем на величины соответствующих уступок.
,
т.е. первые два критерия отличаются
от своих оптимальных значений не больше,
чем на величины соответствующих уступок.
Результат оптимизации при таком переходе в значительной степени определяется величинами уступок. Считается, что ЛПР назначает их в соответствии с уровнями притязаний по каждому критерию.
Пример 3-4. Рассмотрим задачу определения срока профилактической замены критического узла авиационного двигателя, оптимального по критериям: u1 - стоимость замен критического узла, отнесенная к единице времени (руб/час); u2 - вероятность безотказной работы двигателя в промежутке между заменами; u3 - коэффициент готовности критического узла к работе; u4 - ожидаемые потери от отказа критического узла ( руб ) .
К ритерии
u2
и u3
подлежат максимизации, а критерии u1
и u4
- минимизации. Отказы технических
устройств обычно подчинены
показательному распределению. Зависимости
значений критериев от промежутка
между заменами tp,
показаны на рис.3-4.
ритерии
u2
и u3
подлежат максимизации, а критерии u1
и u4
- минимизации. Отказы технических
устройств обычно подчинены
показательному распределению. Зависимости
значений критериев от промежутка
между заменами tp,
показаны на рис.3-4.
Рис.3-4.
К задаче определения срока замены
критического узла авиационного двигателя
Проектировщик упорядочил критерии по важности таким образом: u1, u3, u2, u4, считая, что u1 абсолютно важнее всех остальных критериев, u3 абсолютно важнее критериев u2 и u4, а u2 абсолютно важнее u4. На первом шаге найдем оптимальное значение критерия u1. Из рис.3-4 имеем:
![]() .
.
Пусть проектировщик считает, что критерий
u1
имеет вполне удовлетворительное
значение при u1
30
р/час. Тогда на шаге 2 из рис.3-4 найдем,
что tp
940 и
![]() .
.
Поскольку проектировщика устраивает значение u3 940, то на шаге 3, решив задачу: найти

получим
![]() .
Значение критерия u2
проектировщик не счел
возможным уменьшить. Поэтому окончательно
имеем
.
Значение критерия u2
проектировщик не счел
возможным уменьшить. Поэтому окончательно
имеем
![]() ,
что дает
,
что дает
![]()
2. Аддитивные критерии. Во многих случаях сравнительно просто выразить оценки по каждому отдельному критерию в виде оценок, приведенных к единой (общей) шкале (обычно для этой цели используют денежные или другие традиционные единицы измерений). Если полученные оценки можно считать аддитивными, n целевых функций можно заменить одной целевой функцией (называемой также функцией ценности), имеющей следующий вид:
![]() .
.
На этом основании во многих исследованиях принято использование взвешенных сумм вида
![]() .
.
где величины pi положительны, их сумма равна единице, а сами они рассматриваются как соответствующие веса или коэффициенты относительной важности используемых критериев.
Если приведение к одной единице измерения невозможно, целевая функция образуется путем сложения нормированных значений частных критериев
![]() ,
,
где wi – функции, принимающие значения в интервале от 0 до 1.
Частные критерии имеют различную физическую природу и в соответствии с этим — различную размерность. Именно поэтому при образовании обобщенного критерия следует оперировать не с «натуральными» критериями, а с их нормированными значениями. Нормированные критерии представляют собой отношение «натурального» частного критерия к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам критерий. При этом выбор нормирующего делителя должен быть логически обоснован.
Например, существует подход, в котором предполагается выбирать в качестве нормирующих делителей максимальные значений критериев, достигаемые в области существования решений. Возможен подход, при котором в качестве нормирующих делителей выбирают разность между максимальным и минимальным значениями критерия.
В этих случаях целевая функция задачи принятия решения при применении аддитивного критерия приобретает вид
![]() ,
,
здесь pi
– весовой коэффициент i-ro
частного критерия;
![]() –
i-й
нормирующий делитель.
–
i-й
нормирующий делитель.
Выбор подхода к формированию безразмерной формы частных критериев в значительной степени носит субъективный характер и должен обосновываться в каждом конкретном случае.
Нормированная функция позволяет осуществлять компромисс, при котором улучшение значения одного нормированного частного критерия компенсирует ухудшение значений других. Введение весовых коэффициентов должно учитывать различную значимость частных критериев при формировании аддитивного критерия. Определение весовых коэффициентов сталкивается с серьезными трудностями и обычно сводится либо к использованию формальных процедур, либо к применению экспертных оценок.
С появлением обобщенного критерия исчезают логические проблемы, связанные с установлением взаимосвязей между частными критериями различной размерности и выбором наилучшего варианта проектируемого объекта, и остаются лишь вычислительные трудности.
Но аддитивный критерий имеет ряд недостатков, главный из которых состоит в том, что он не вытекает из объективной роли частных критериев в функционировании цели и выступает поэтому как формальный математический прием, придающий задаче удобный для решения вид. Другой недостаток заключается в том, что в аддитивном критерии может происходить взаимная компенсация частных критериев. Это значит, что значительное уменьшение одного из критериев вплоть до нулевого значения может быть покрыто возрастанием другого критерия. Для ослабления этого недостатка следует вводить ограничения на минимальные значения частных критериев и их весовых коэффициентов.
Несмотря на слабые стороны обобщенный аддитивный критерия позволяет в ряде случаев успешно решать многокритериальные задачи и получать полезные результаты.
3. Мультипликативные критерии.
Очевидно, что класс функций
![]() ,
которые могут использоваться для
агрегирования нескольких целевых
функций в одну, не ограничивается
аддитивными выражениями. Все они, по
существу, аналогичны, хотя и несут
различную функциональную нагрузку.
,
которые могут использоваться для
агрегирования нескольких целевых
функций в одну, не ограничивается
аддитивными выражениями. Все они, по
существу, аналогичны, хотя и несут
различную функциональную нагрузку.
Аддитивные критерии основаны на использовании принципа компенсации абсолютных значений нормированных частных критериев. Но в ряде задач проектирования более целесообразным является оперирование не с абсолютными, а с относительными изменениями значений частных критериев.
Принцип относительной компенсации формулируется следующим образом: справедливым следует считать такой компромисс, когда суммарный уровень относительного снижения значений одного или нескольких критериев не превышает суммарного уровня относительного увеличения значений других критериев.
Мультипликативный критерий образуется путем простого перемножения частных критериев в том случае, если все они имеют одинаковую важность. В случае неравноценности частных критериев вводятся весовые коэффициенты ci и мультипликативный критерий принимает вид
![]() .
.
Достоинством мультипликативного критерия является то, что при его использовании не требуется нормировка частных критериев.
Недостатки критерия: критерий компенсирует недостаточную величину одного частного критерия избыточной величиной другого и имеет тенденцию сглаживать уровни частных критериев за счет неравнозначных первоначальных значений частных критериев.
Пример 3-5. Проектирование технологического оборудования. Переносной автомат для забивания стальных дюбелей в бетонные стены состоит из корпуса с магазином, содержащим запас дюбелей, подающе-спускового механизма с зарядами и ствола. Требуется определить основной конструктивный параметр автомата — длину ствола L — при следующих исходных данных: число дюбелей, помещающихся в магазине, N 12, масса одного дюбеля с расходуемым на него зарядом m=50 г, масса ствола 1,6 кг/м, масса корпуса 2 кг, критерий оптимальности — минимальная масса заряженного автомата.
Рис.3-5. Область
решения задачи оптимизации
технологического автомата
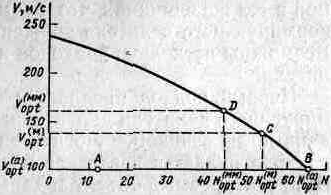
При фиксированной величине заряда и
заданной массе дюбеля скорость V
выбрасывания дюбеля связана
с длиной ствола L
соотношением
![]() ,
где
,
где
![]() .
Минимально допустимая скорость дюбеля
определяется экспериментально: Vmin=100
м/с. Масса автомата при минимально
допустимом числе дюбелей в магазине
определяется как F(L)
= 1,6
L+0,05 N
+ 2 = 1,6L+2,6.
.
Минимально допустимая скорость дюбеля
определяется экспериментально: Vmin=100
м/с. Масса автомата при минимально
допустимом числе дюбелей в магазине
определяется как F(L)
= 1,6
L+0,05 N
+ 2 = 1,6L+2,6.
Задача проектирования автомата сводится
к минимизации целевой функции F(L)
= 1,6L+2,6
при ограничении
![]() .
.
Решение задачи оптимизации имеет вид: L=0,445M, F(L)=3,31 кг. График области компромисса для массы автомата 6 кг показан на рис.3.5. Здесь точка А соответствует оптимальному решению данной задачи по критерию минимума массы автомата.
Пример 3-6. По исходным данным примера 3-5 определить конструктивные параметры L и N переносного автомата при условии, что масса заряженного автомата не должна превышать 6 кг, а частными критериями эффективности автомата являются скорость выбрасывания дюбеля V и число дюбелей N, помещающихся в магазине. Выбор этих критериев объясняется тем, что чем выше V, тем надежнее дюбеля проникают в бетон любой марки, а чем больше N, тем удобнее работать с автоматом. По мнению экспертов оба критерия V и N в нормированном виде имеют одинаковую важность.
Найдем оптимальное решение с помощью аддитивного критерия. Для нормирования найдем Nmax и Vmax. Величину Nmax определяют из условия, Vmin=100м/с. Уравнение баланса масс имеет вид
1,6L+0,05N+2=6.
Из этого уравнения следует, что Nmax=65.
Для отыскания Vmax будем считать, что в
автомате находится только один дюбель.
Тогда
![]() м/с.
Нормированные частные критерии будут
иметь вид u1(V)=V/236;
u2(N)=N/65.
м/с.
Нормированные частные критерии будут
иметь вид u1(V)=V/236;
u2(N)=N/65.
Аддитивный критерий эффективности автомата
F (V, N) = u1(V)+u2(N)=V/236+N/65.
Для определения максимального значения аддитивного критерия F(V, N) с учетом ограничения на массу автомата воспользуемся методом неопределенных множителей Лагранжа. В результате решения задачи оптимизации получаем Vopt=100 м/с, Lopt=0,445м, Nopt=65. На рис.3-5 данному решению соответствует точка В.
Пример 3-7. По исходным данным примера 3-6 определить конструктивные параметры технологического автомата по мультипликативному критерию вида
F (V, N) = VN.
Для отыскания максимума функции F(V, N) составляем функцию Лагранжа
![]() ,
где – множитель
Лагранжа.
,
где – множитель
Лагранжа.
Выражая длину ствола L через скорость V и решая задачу оптимизации, получаем Vopt = 137 м/с, Lopt =0,833 м, Nopt. =53, что соответствует точке С на рис.3-5.
Использование мультипликативного критерия в задаче оптимизации привело к другим значениям параметров технологического автомата по сравнению с решением задачи с аддитивным критерием оптимальности.
Это объясняется тем, что диапазоны взаимной компенсации абсолютных и относительных изменений частных критериев V и N неодинаковы. Поэтому в каждом конкретном случае технического проектирования следует тщательно анализировать и обосновывать целесообразность учета либо абсолютных, либо относительных изменений значений частных критериев и в зависимости от степени важности этих отклонений выбирать либо аддитивный, либо мультипликативный критерий оптимальности.
