24. Равномерное и показательное распределение.

Равномерным распределение называется если мат ожидание (интеграл от b до a x*f(x)) = (a+b)/2 В этом случае дисперсия (интеграл от b до a x^2*f(x)) = (b-a)²/12.

П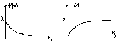 оказательное распределение НСВ Х, принимающая знач >0 имеет показ распр если плотность имее вид: F(x)= {1-e^-λx при х>=0 и =0 при x<0 то есть f(x)=F’(x) f(x) надо написать. При показ распределении:

1) М(х)=1/λ

2) D(x)=1/λ²

3) P(a<=x<b)=e^-λa-e^-λb

25. Норм распределение. Функция Лапласса и его свойства

Нормальный закон.

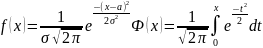- ф-ла Лапласса

Св-ва Ф*(х)

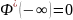
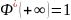
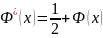
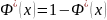
26. Система двух случайных величин, функция распределения и плотность.

Закон распределения дискретной двумерной случайной величины (Х, Y)  имеет вид таблицы с двойным входом, задающей перечень возможных значений каждой компоненты и вероятности p(xi, yj), с которыми величина принимает значение (xi, yj):(рисуем таблицу иксы сверху игреки слево)

При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1.

О пределение . Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y:

F( х, у ) = p ( X < x, Y < y )

27. Дисперсия

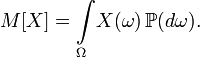
Мат ожидание

Безразмерной характеристикой коррелированности двух случайных величин является коэффи-циент корреляции

Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.

28. Независимость и некоррелированность

Опр. Если ковариация =0 то случ величина называется некоррелированна.

Утв: Х и У некоторые случ велич

М(Х*У)=М(Х)*М(У)

D(X+Y)=D(X)+D(Y)

Опр. R_xy=k_xy/σ_x* σ_y

Cв-ва 1) |r_xy|≤1 r_xy=1 => X,Y линейно не зависимы

2.X и Y – не зависимы => r_xy=0

29. Числовые характеристики системы случайных велечин

Дисперсия

Мат ожидание

Безразмерной характеристикой коррелированности двух случайных величин является коэффи-циент корреляции

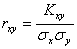
30. Ф-ция случайной величины

Плотность вероятности суммы двух случайных величин ~ Распределение произведения двух случайных величин

 Если  - случайная величина с областью значений X_ и функция f(x) определена на множестве X_ , то  = f(x) - тоже случайная величина. Задача об отыскании функции распределения случайной величины  по известной функции распределения случайной величины  легко решается, если f(x) - непрерывная монотонно возрастающая функция. Доказано, что тогда функция распределения F (x) случайной величины  задается формулой F (x)=F_ ([f(x)]^-1).

Здесь F_ (x) - известная функция распределения случайной величины  , а символом [f(x)]^-1 обозначена функция, обратная к функции f(x).

Плотность распределения случайной величины  для дифференцируемой f(x) вычисляется по формуле .

Плотность вероятности суммы двух случайных величин

 В теории вероятностей часто возникает необходимость в определении плотности вероятности суммы двух независимых случайных величин. Если  ₁ и  ₂ - непрерывные независимые случайные величины с плотностями вероятности соответственно p₁(x) и p₂(x), то плотность вероятностей суммы  =  ₁ +  ₂ вычисляется по формуле: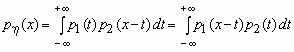 .