
- •1. Элементы комбинаторики. Перестановки. Размещения. Сочетания (без повторений).
- •2. Случайные события. Классификация случайных событий. Действия над случайными событиями.
- •Действия над случайными событиями.
- •3. Классическое определение вероятности случайного события. Свойства вероятности.
- •Свойства вероятности:
- •4. Совместные и несовместные случайные события. Теоремы сложения вероятностей совместных и несовместных случайных событий.
- •5. Условные вероятности. Свойства условных вероятностей.
- •6. Зависимые и независимые случайные события. Теоремы умножения вероятности зависимых и независимых случайных событий.
- •7. Полная группа событий. Формула полной вероятности. Формула Байеса.
- •Формула полной вероятности
- •Формула Байеса
- •8. Повторные независимые испытания. Формула Бернулли.
- •9. Повторные независимые испытания. Формула Пуассона. Условия применимости формулы Пуассона.
- •10. Определение дискретной случайной величины. Закон распределения дискретной случайной величины. Математическое ожидание дискретной случайной величины. Свойства математического ожидания.
- •11. Определение дискретной случайной величины. Закон распределения дискретной случайной величины. Дисперсия дискретной случайной величины. Свойства дисперсии. Среднее квадратическое отклонение.
- •12. Определение непрерывной случайной величины. Функция распределения непрерывной случайной величины. Свойства функции распределения непрерывной случайной величины.
- •Свойства функции распределения для непрерывной случайной величины:
- •13. Определение непрерывной случайной величины. Плотность распределения непрерывной случайной величины. Основные свойства плотности распределения.
- •14. Математическое ожидание и дисперсия непрерывной случайной величины. Определение и основные свойства.
- •Свойства дисперсии.
- •15. Равномерное распределение. Плотность распределения. Функция распределения. Математическое ожидание и дисперсия равномерно распределенной случайной величины.
- •16. Биноминальное распределение. Математическое ожидание и дисперсия равномерно распределенной случайной величины.
- •17. Показательное распределение. Плотность распределения. Функция распределения. Математическое ожидание и дисперсия показательно распределенной случайной величины.
- •18. Нормальное распределение. Плотность распределения. Математическое ожидание и дисперсия нормально распределенной случайной величины. График нормального распределения.
- •19. Закон больших чисел.
- •20. Предмет математической статистики. Генеральная совокупность. Выборочный метод. Репрезентативная выборка.
- •22. Статистическое оценивание. Точечные оценки. Выборочное среднее и выборочная дисперсия.
- •23. Статистическое оценивание. Интервальные оценки. Доверительный интервал для оценки математического ожидания нормально распределенной случайной величины.
20. Предмет математической статистики. Генеральная совокупность. Выборочный метод. Репрезентативная выборка.
Выборочный метод – это один из основных методов математической статистики.
Одной из центральных задач математической статистики является выявление закономерностей в статистических данных, на базе которых можно строить соответствующие модели и принимать обдуманные решения. Под статистическими данными подразумеваются данные наблюдений за значениями некоторой случайной величины или совокупности случайных величин, характеризующих изучаемый процесс.
Первая задача математической статистики – указать способы сбора и группировки статистических данных, полученных в результате наблюдений или испытаний.
Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования. Элементами такого анализа являются:
а) оценки неизвестной вероятности события, неизвестной функции распределения, неизвестных параметров известного распределения, зависимости двух или нескольких случайных величин и т. п.;
б) проверка статистических гипотез о виде неизвестного распределения; о величинах параметров известного распределения; о виде и силе зависимости между рассматриваемыми случайными величинами.
Таким образом, основная задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Генеральной совокупностью называется множество всех возможных значений или реализаций исследуемой случайной величины X при данном реальном комплексе условий. Выборкой (выборочной совокупностью) называют часть генеральной совокупности, отобранную для изучения. Число элементов рассматриваемой совокупности называется ее объемом.
Репрезентативная выборка – это такая выборка, в которой все основные признаки генеральной совокупности, из которой извлечена данная выборка, представлены приблизительно в той же пропорции или с той же частотой, с которой данный признак выступает в этой генеральной совокупности.
21. Вариационные и интервальные ряды. Полигон и гистограмма. Эмпирическая функция распределения. Вариационные ряды – это раздел математической статистики – науки о методах обработки результатов наблюдений массовых случайных явлений в социальных, экономических и технических системах. Интервальным вариационным рядом называют упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений величины. Для построения интервального ряда необходимо: 1. определить величину частичных интервалов; 2. определить ширину интервалов;
3.
установить для каждого интервала
его верхнюю и нижнюю
границы;
4. сгруппировать результаты наблюдении.
Полигоном
частот
называют ломанную, отрезки которой
соединяют точки (x1,
n1),
(x2,
n2),..(xk,
nk),
где xi
– варианты выборки и ni
– соответствующие им частоты. Полигоном
относительных частот
называют ломанную, отрезки которой
соединяют точки (x1,
w1),
(x2,
w2),..(xk,
wk),
где xi
– варианты выборки и wi
– соответствующие им относительные
частоты. Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат интервалы длины h, а высоты равны
отношению n1/h
(плотность частоты). Площадь гистограммы
частот равна сумме всех частот, т.е.
объему выборке n. Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат интервалы длины h, а высоты равны
отношению w1/h
(плотность относительной частоты).
Площадь гистограммы относительных
частот равна сумме всех относительных
частот, т.е. единице. Эмпирическая
функция распределения. 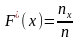 По
статистическому ряду можно построить
эмпирическую
функцию
распределения F*
(х): где
пх
—
число значений случайной величины X,
меньших,
чем
х;
п —
объем выборки. По
определению F*(x)
обладает
следующими свойствами:
1.
ее значения принадлежат от 0 до 1, т.е. 0
F*(x)
1. 2.
Для любых х1
< х2,
F*(x1)
F*(x2),
т.е.
не убывающая. 3.
F*(x)
= 0 при х
х1;
F*(x)
= 1 при х
>
xk.
Эмпирическая
функция распределения F*(х)
является
оценкой функции распределения F(x)
=
Р(Х
< х), которая
в этом случае
называется теоретической функцией
распределения
По
статистическому ряду можно построить
эмпирическую
функцию
распределения F*
(х): где
пх
—
число значений случайной величины X,
меньших,
чем
х;
п —
объем выборки. По
определению F*(x)
обладает
следующими свойствами:
1.
ее значения принадлежат от 0 до 1, т.е. 0
F*(x)
1. 2.
Для любых х1
< х2,
F*(x1)
F*(x2),
т.е.
не убывающая. 3.
F*(x)
= 0 при х
х1;
F*(x)
= 1 при х
>
xk.
Эмпирическая
функция распределения F*(х)
является
оценкой функции распределения F(x)
=
Р(Х
< х), которая
в этом случае
называется теоретической функцией
распределения
