§6. Классификация как задача статистической

проверки гипотез

Рассматривается классификация в режиме с обучением. Для простоты и наглядности положим k = 2, p = 2. Классы _{1 ,} ₂ представлены своими обучающими выборками (2.9). Кроме того, известен закон распределения вероятностей значений признаков в каждом классе, т.е. заданы функции распределений вероятностей [4]:

, .

Предположим, что

, ,

где f₁(X), f₂(X) – функции плотностей вероятностей в классах _{1 ,} ₂ соответственно (рис. 2.10).

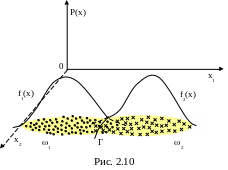
Наблюдаемый объект может принадлежать только одному из двух классов ₁ или ₂ . Необходимо сформулировать правило, по которому вектор X был бы отнесен к ₁ или к ₂ с минимальной вероятностью ошибки классификации P_ош.

В сформулированных выше условиях задача классификации сводится к задаче статистической проверки двух гипотез H₁ и H₂,

,

.

В процессе принятия решения возможны ошибки 1-го и 2-го родов. Вероятность ошибки 1-го рода – вероятность отклонить гипотезу Н₁ в то время, когда она истинна. Вероятность ошибки 2-го рода – вероятность принять гипотезу Н₂ в то время, когда истинной является гипотеза Н₁. Эти два вида ошибок часто неодинаково важны для лица, принимающего решение. Поэтому вводятся цены ошибок 1-го и 2-го рода. Пример из гидролокации: пусть ₁ – множество сигналов, создаваемых подводной лодкой, ₂ – множество других морских сигналов, не создаваемых подводной лодкой. Ошибка 1-го рода – пропустить сигнал подводной лодки (пропуск цели), ошибка 2-го рода – принять морской шум за сигнал подводной лодки (ложная тревога). В этом случае ошибка 1-го рода имеет бóльший вес, чем ошибка 2-го рода.

Пусть c₁ – цена ошибки 1-го рода, c₂ – цена ошибки 2-го рода, ₁ – априорная вероятность класса ₁, ₂ – априорная вероятность класса ₂, ₁+₂=1 (₁ – вероятность того, что любое наблюдение Х₁ без учета функции распределения F₁(X)). Проекция линии пересечения поверхностей f₁(x) и f₂(x) на плоскость R делит ее на две полуплоскости R₁ и R₂,

R=R₁ R₂, R₁ R₂= .

Тогда, если наблюдаемый вектор XR₁, то X будет отнесен к классу ₁, а если X , то X будет отнесен к классу ₂. Вычислим вероятность правильной и неправильной классификаций вектора X. Если X₁, то вероятность его правильной классификации равна

,

а вероятность его неправильной классификации равна

. (2.20)

Аналогично, если X₂, то вероятности его правильной и неправильной классификации равны соответственно

,

. (2.21)

Вероятность ошибки 1-го рода задается формулой (2.20), вероятность ошибки 2-го рода – формулой (2.21). В соответствии с теорией статистических решений целесообразно ввести решающее правило

классификации, минимизирующее риск [4]

.

Используя выражения (2.20), (2.21), имеем

. (2.22)

Так как

, R₂ = R \ R₁,

то первый интеграл в выражении (2.22) представим в виде

. (2.23)

На основании равенства (2.23) выражение (2.22) преобразуется к виду

.

Так как , то необходимым условием минимума функции  является отрицательность подынтегральной функции,

.

Из последнего выражения имеем

,

или

. (2.24a)

Правая часть в (2.24а) –– коэффициент подобия

,

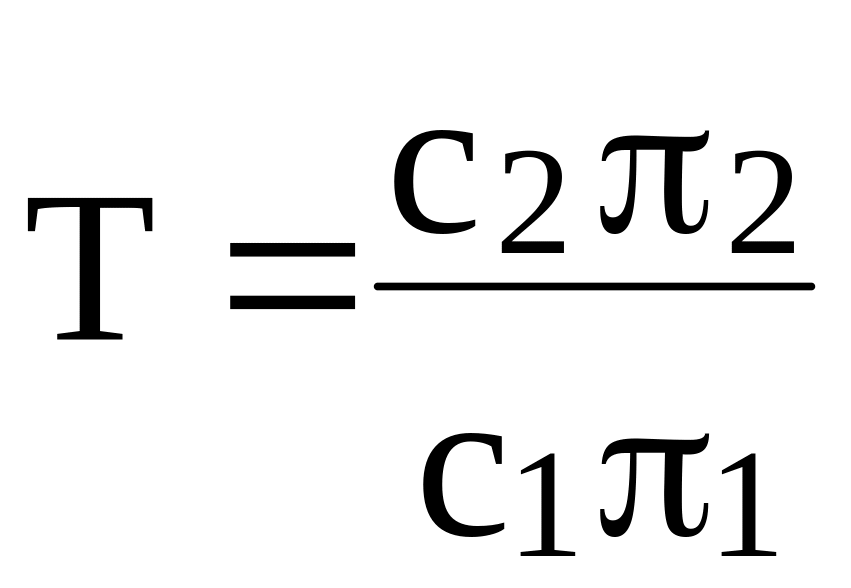который является постоянным для данного выбора с₁, с₂. Если , то Т=1 . Если имеет место неравенство (2.24а), то наблюдаемый вектор Х относится к классу ₁. Если выполняется неравенство

, (2.24б)

то наблюдаемый вектор Х относится к классу ₂. Если выполняется равенство

, (2.24в)

то наблюдаемый вектор Х относится к одному из классов ₁, ₂. Уравнение (2.24в) –– уравнение границы классов _1, _2. Сформулированное решающее правило относится к так называемым правилам Байеса [4,7].

Провести классификацию наблюдаемого вектора Х можно и по другому правилу, по максимуму его апостериорной вероятности. При условиях нашей задачи можно вычислить апостериорную вероятность , принадлежности вектора Х к классу _i [7]:

.

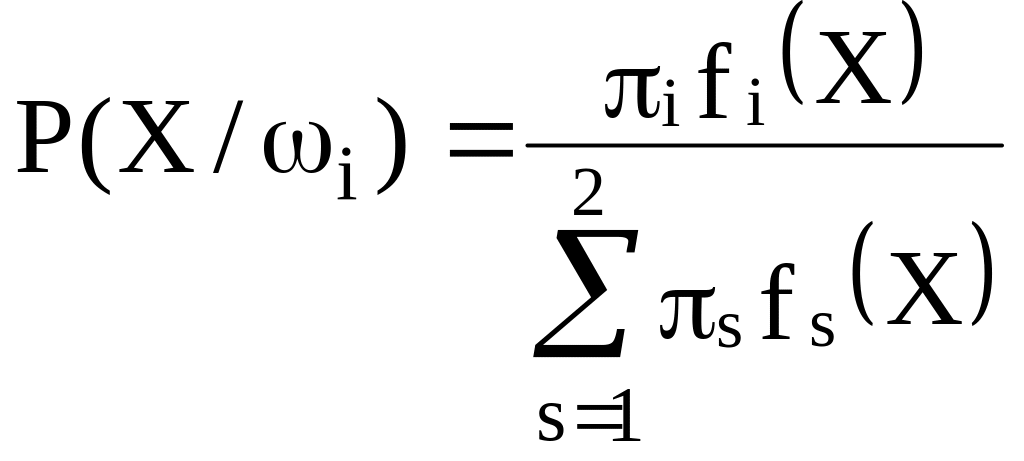Тогда вектор Х относится к тому классу , для которого значение апостериорной вероятности максимально. (2.7). Это правило не учитывает цен ошибок 1–го и 2–го родов .

К описанной здесь методике удается свести многие практические задачи, формулируя их в терминах статической теории решений. Полезность этой теории и ее методов ограничивается допущением, что плотности вероятностей известны. В некоторых случаях это действительно имеет место.

Если функции неизвестны, то получают их оценки по обучающим выборкам аппроксимационными метода-ми [4,7]. Распознание базируется на сопоставлении уже полученных оценок для исследуемого объекта Х пространства R по правилам [2.24].

Байесовское решающее правило принимает простой вид в случае, когда –– плотности вероятностей нормальных распределений с равными ковариационными матрицами  и различными векторами средних значений _i [7,9] :

.

В этом случае уравнением границы (2.24в) является линейная функция. Прологарифмировав равенство (2.24в),

, (2.25)

и проведя в его левой части умножения матриц, после приведения подобных членов с учетом (2.25) получим линейное уравнение

.

Первое слагаемое в левой части последнего равенства называется линейной дискриминантной функции Фишера [9],

.

Неравенство (2.24а) в этом случае принимает вид

Область наилучшей классификации определяется так:

, (2.26а)

. (2.26б)

В случае неизвестных параметров распределений находят их оптимальные оценки по обучающим выборкам (2.9) [7]:

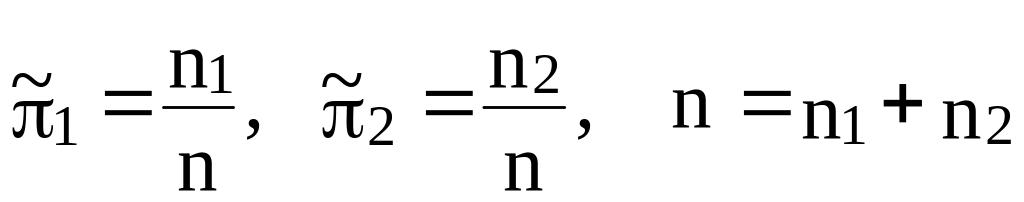, (2.27а)

, (2.27б)

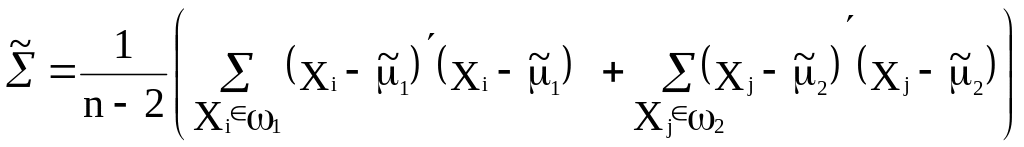. (2.27в)

Оценка ковариационной матрицы в (2.27в) получена по двум обучающим выборкам (2.9). Оценки параметров в (2.27) используются в правилах классификации (2.26). Области наилучшей классификации определяются неравенствами

,

.

Формирование правил классификации для принципиально не отличаются от рассмотренной нами ситуации двух классов. Классификационные функции принимают вид [4,7]

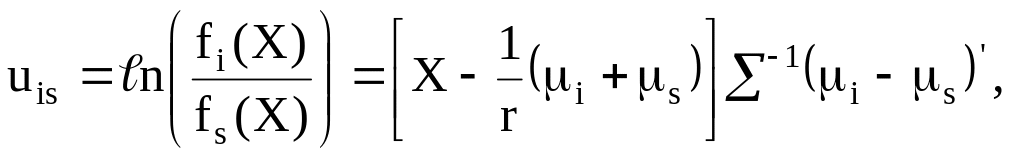i,s = 1,2,…,k.

Области оптимальной классификации определяются из неравенств

Классификационная функция связана с i-м и s-м классами. Так как каждая такая функция линейна, то область R_i ограничена гипер-плоскостями (рис. 2.11 ) .

Линейная дискриминантная функция (ЛДФ) широко используется в медицинской диагностике (МД). Сотни коллективов во всем мире работают над проблемой автоматизации МД. Испытаны различные математические методы, разные эвристические подходы, моделирующие деятельность врача. По ряду соображений наиболее перспективным методом в решении такой задачи является использование ЛДФ [10].

Для удобства в выражениях (2.26) введем обозначения:

,

.

Тогда неравенство (2.26) – правило классификации примет вид

,

где X=(x₁,x₂,…,x_p) – симптомы, признаки отдельного пациента, W’ – коэффициенты, учитывающие диагностическую ценность признаков. Для исследуемого пациента Х имеем

.

Чтобы отнести пациента Х к одному из классов ₁ (рак) или к ₂ (не рак) достаточно сравнить полученное значение (Х,W’) с пороговым значением и принять решение:

₁, если (,W’)> a ,

₂, если (,W’) a.

Значение параметров W, a вычисляются по картам обследования пациентов в поликлинике из класса ₁ и класса ₂.