§8. Предварительное обнаружение классов

и оценивание их числа

Результаты классификации реальных объектов, проводимой при помощи математических методов и алгоритмов, зависят как от используемых методов, так и от пороговых значений параметров конкретного метода. При этом не исключено формальное разделение исследуемого множества объектов на группы, не являющиеся классами. Поэтому до проведения классификации необходимо знать, а имеет ли данное множество наблюдений классы или оно однородно (т.е. представляет собою один класс). Кроме того, полезно иметь такую информацию о структуре этого множества, как: степень удаленности классов друг от друга, их количество, их диаметры, центры тяжести классов, существование различия в плотностях точек классов и др. [12]. Получение такой информации намного упростит решение конкретной задачи классификации, например поможет выбрать оптимальный алгоритм классификации, точно задать пороговые значения, что сократит объем работ.

Такой предварительный анализ структуры данного множества проводится по гистограммам расстояний между всеми его точками. Исследование гистограмм данного множества наблюдений целесообразно изложить, начиная с одномерного случая.

8.1. Одномерное пространство

Пусть множество Х⁽ⁿ⁾ представляет собой одномерную выборку (р = 1) :

(2.32a)

с плотностью вероятности [8, 9]. Упорядочив элементы множества Х⁽ⁿ⁾ по возрастанию

, (2.32б)

получим вариационный ряд (ВР). Значения x₍₁₎, x_(n) отложим на числовой оси, отрезок [x₍₁₎, x_(n)] разделим на t равных частей, t  3 (рис. 2.15). Длина каждого полученного отрезка (x_i, x_i+1), i = 1, 2, …, t равна

.

Пусть n_i – число членов ВР (2.32б), попавших в i-й полуинтервал [x_i, x_i+1), i = 1, 2, …, t. Тогда оценка вероятности p_i попадания в i-й полуинтервал случайной величины  равна

. (2.33)

Построим в каждом полуинтервале [x_i, x_i+1), прямоугольник с высотой h_i и основанием  такой, чтобы его площадь S_i,

, (2.34)

была равна в (2.33).

. (2.35)

Из равенств (2.33) – (2.35) имеем

.

Так строится гистограмма плотности вероятности f(x) данных наблюдений, один из видов которой представлен на рис. 2.15. Отметим, что последним из полученных интервалов гистограммы должен быть отрезок [x_t, x_t+1], x_t+1 = x_(n), x₁ = x₍₁₎.

Число интервалов, на которые делится отрезок [x₍₁₎, x_(n)], задается исследователем. Эти интервалы могут быть разной длины.

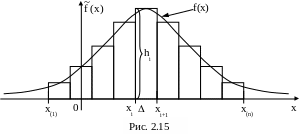
При увеличении объема наблюдений n и уменьшении длины интервала  гистограмма стремится к функции ,

.

Если исследуемое множество (2.32) состоит из классов, далеко отстоящих друг от друга (рис. 2.16), то его гистограмма имеет достаточно глубокий локальный минимум (ЛМ), изображенный на рис. 2.17.

Пусть ЛМ наблюдается в промежутке [x_q, x_q+1]. Фиксируются два ближайших к нему максимума, из которых выделяется наименьший, наблюдаемый в промежутке [x_u, x_u+1). Далее исследуется [x_q, x_u+1) полуинтервал.

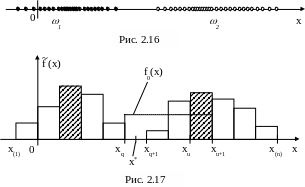
Определение 2.1. ЛМ гистограммы называется статистически значимым (СЗЛМ), если на отрезке [x_q, x_u+1] отвергается гипотеза H₀ о равномерном распределении подвыборки множества (2.32), принадлежащей полуинтервалу [x_q, x_u+1). H₀: f(x) = f₀(x)_­,

Определение 2.2. ЛМ гистограммы называется статистически незначимым, если на отрезке [x_q, x_u+1] принимается гипотеза H₀ о равномерном распределении подвыборки множества (2.32), принадлежащей [x_q, x_u+1).

Проверка гипотезы Н₀ проводится с использованием известных статистических критериев ², ², Вилкоксона, знаков и др. [12].

Если гистограмма исследуемого множества имеет хотя бы один СЗЛМ, то это множество содержит классы, далеко отстоящие друг от друга. Число классов k оценивается по числу СЗЛМ гистограммы :

.

Число далеко удаленных друг от друга классов определяется равенством

.

За границы классов принимаются середины тех отрезков гистограммы, в которых наблюдается ее СЗЛМ [6, 12]. На рис. 2.17 точка x^* – граница классов ₁, ₂.

Если гистограмма исследуемого множества наблюдений не имеет ЛМ (рис. 2.15) или все ее ЛМ статистически незначимы (рис. 2.18), то это множество однородно, т.е. представляет собою один класс, или содержит классы, недалеко отстоящие друг от друга.

8.2. Многомерное пространство

Если число признаков p каждого объекта данного множества наблюдений (2.28) p  2, то предварительную информацию о наличии классов, их числе, степени их удаленности друг от друга и др. можно получить, по крайней мере, тремя способами.

1. Построение и анализ гистограммы каждого признака x_s, s = 1, 2, …, p [6, 8]. Каждая такая гистограмма может дать оценку снизу для числа классов k, , m_s – число СЗЛМ гистограммы s-го признака. Тогда имеем

.

2. Построение и анализ многомерных гистограмм. Строятся t p-мерных интервалов, t = t₁t₂…t_p, t_s – число интервалов, на которое разбиваются значения ­s-го признака, s = 1, 2, …, p. Подсчитывается число точек множества (2.28), попавших в каждый p-мерный интервал n_i, i = 1, 2, …, t. Затем выделяются интервалы, содержащие наибольшее число точек, по правилу n_i  n₀, n₀ – некоторое заданное пороговое значение. Вычисляются центры тяжести таких интервалов, эти интервалы объединяются в один класс по расстоянию между их центрами по правилу «ближний к ближнему». Кроме того, фиксируются интервалы, содержащие наименьшее число точек, , – другое пороговое значение. По таким интервалам проводятся границы между классами [6]. Интервалы, для элементов которых имеет место неравенство , объединяются с интервалами с наибольшим содержанием точек по правилу «ближний к ближнему». Предварительный анализ многомерных интервалов – очень трудоемкий процесс, практически не осуществимый при больших значениях n и p.

3. Анализ одномерной гистограммы расстояний между всеми различными точками данного множества [12]. Рассмотрим этот метод подробно.

На множестве x⁽ⁿ⁾ в (2.28) задается подходящее расстояние r (метрика) и находятся расстояния между всеми его точками r_ij = r(x_i, x_j), i, j = 1,2, …, n, которые можно записать в виде квадратной матрицы

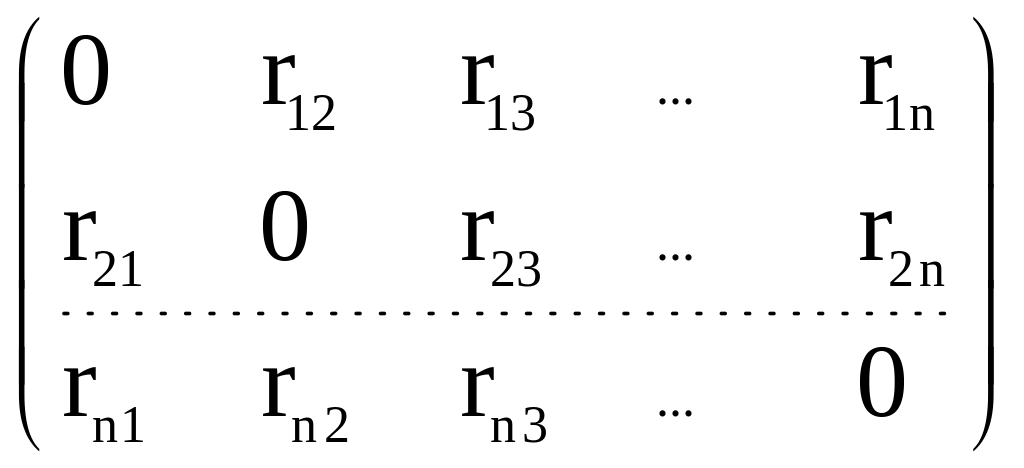. (2.36)

В силу свойств расстояния имеем

r_ii = 0, r_ij= r_ji, i,j = 1, 2, …, n.

Поэтому в матрице (2.36) достаточно исследовать множество элементов, стоящих выше или ниже главной диагонали, например

. (2.37)

Упорядочив элементы множества (2.37) по возрастанию, получим основной вариационный ряд (ОВР) множества X⁽ⁿ⁾

r₍₁₎  r₍₂₎  …  r_(s) , (2.38)

Сначала предположим, что плотности классов множества Х⁽ⁿ⁾ статистически равны, т.е. отличаются незначительно. Очевидно, если множество Х⁽ⁿ⁾ имеет классы, далеко отстающие друг от друга, то гистограмма его ОВР имеет хотя бы один СЗЛМ.

Определение 2.3. Пара точек однородна, если эти точки принадлежат одному какому-то классу _s, X_i, X_j  _s, s {1,2, …, k}.

Определение 2.4. Пара точек (X_i, X_j) неоднородна, если эти точки принадлежат разным классам, X_i  _s, X_j  _t, s = t, s, t {1,2, …, k}.

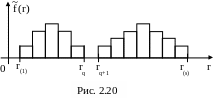
На рис. 2.19 изображено множество Х⁽ⁿ⁾, состоящее из трех классов, далеко отстоящих друг от друга. Гистограмма ОВР множества Х⁽ⁿ⁾ имеет один СЗЛМ (рис. 2.20), наблюдаемый на отрезке [r_q, r_q+1].

Расстояние между точками каждой однородной пары меньше расстояния между точками каждой неоднородной пары ,

< ,

так что некоторая точка отрезка [r_q, r_q+1] является границей множеств расстояний между точками однородных пар { } и неоднородных пар { }. Левый конец отрезка [r_q, r_q+1] можно считать оценкой (приближенным значением) наибольшего диаметра классов d_max,

. (2.39)

На рис. 2.21. представлено множество Х⁽ⁿ⁾, состоящее из трех классов, далеко отстоящих друг от друга. Гистограмма ОВР такого множества имеет два СЗЛМ (рис. 2.22). Первый СЗЛМ (нумерация идет слева направо) наблюдается в промежутке [r_q, r_q+1]. Расстояние между точками почти каждой однородной пары лежит на отрезке [r₁, r_q], а расстояния между точками каждой неоднородной пары лежат на отрезке [r_q+1, r_(s)], причем на отрезке [r_q+1, r_u] находятся расстояния между точками из классов ₁, ₂ и ₂, ₃, а на отрезке [r_u+1, r_(s)] – расстояния между точками из классов ₁, ₃.

Можно привести пример, когда гистограмма ОВР множества Х⁽ⁿ⁾, состоящего из трех далеко отстоящих друг от друга классов имеет три СЗЛМ [12].

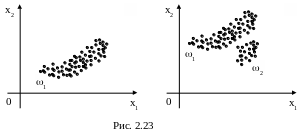
Если данное множество Х⁽ⁿ⁾ однородно или состоит из классов, близко расположенных друг другу (рис. 2.23), то гистограмма его ОВР не содержит ни одного СЗЛМ и имеет вид, аналогичный представленным на рис. 2.15, 2.18.

Из наших рассуждений делаем следующие выводы:

1. Если гистограмма ОВР данного множества Х⁽ⁿ⁾ имеет хотя бы один СЗЛМ, то в этом множестве есть классы, далеко отстоящие друг от друга, и оценка наибольшего диаметра таких классов определяется равенством (2.39).

2. Если гистограмма ОВР данного множества Х⁽ⁿ⁾ не имеет ни одного СЗЛМ, то это множество однородно или состоит из классов, близко расположенных друг к другу.

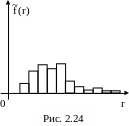
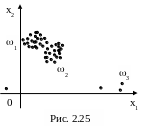
3. Если гистограмма ОВР имеет «длинный хвост», то множество Х⁽ⁿ⁾ содержит резко выделяющиеся наблюдения (рис. 2.24), которые можно считать классами с малым числом элементов (рис. 2.25).

О тметим, что исследование структуры множества Х⁽ⁿ⁾ по ОВР можно проводить и в одномерном случае, предварительно задав на этом множестве подходящую метрику.

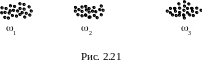
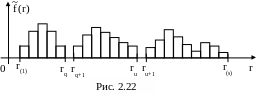
а

б

8.3. Оценивание числа классов

Полагаем, что классы исследуемого множества имеют статистически (почти) равные плотности точек, а на гистограмме ОВР этого множества наблюдается хотя бы один СЗЛМ (рис. 2.22).

Оценим число классов k множества Х⁽ⁿ⁾ по числу СЗЛМ гистограммы его ОВР. Пусть - число наблюдаемых СЗЛМ на гистограмме ОВР, а m – максимальное число СЗЛМ этой гистограммы, которое обусловлено наличием k классов, далеко отстоящих друг от друга. Очевидно,

.

Тогда

.

Решая это квадратное неравенство, получим

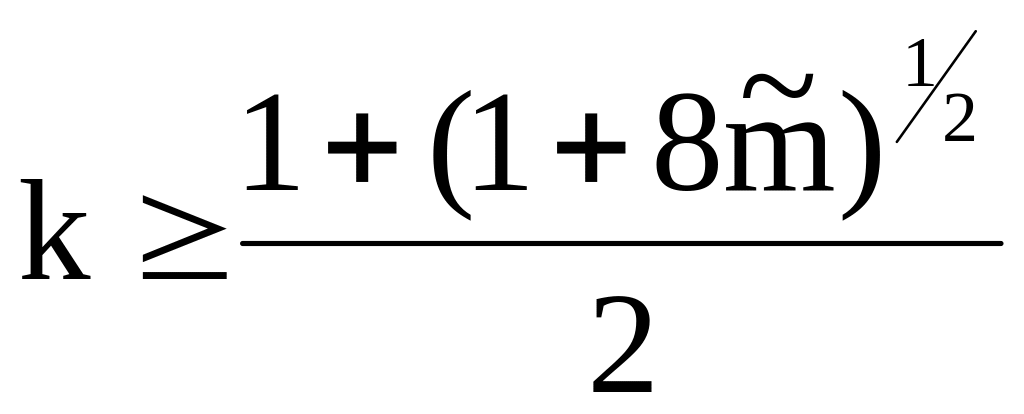. (2.40)

Переходя в неравенстве (2.40) к целочисленным решениям, получим

, (2.41)

где  – малое положительное число, Е[Y] – целая часть Y.

Оценку снизу для числа классов можно получить другим способом, по числу однородных пар. Число пар точек множества Х⁽ⁿ⁾ равно n², пусть n₀ – число его однородных пар. Тогда оценка вероятности того, что произвольная пара (X_i, X_j) точек множества Х⁽ⁿ⁾ однородна, равна

. (2.42)

Оценим число однородных пар по ОВР. На гистограмме ОВР фиксируем первый СЗЛМ (нумерация идет слева направо), на рис. 2.22 первый СЗЛМ обнаруживается на отрезке [r_q, r_q+1]. Очевидно, все r_(i) ОВР, которые удовлетворяют неравенству

r_(i)  r_q , i = 1, 2, …, i₀,

являются расстояниями между точками однородной пары. Тогда число однородных пар, оцениваемое по ОВР, равно i₀,

.

Учитывая, что в ОВР входят лишь все те элементы матрицы (2.36), которые стоят выше ее главной диагонали, имеем

, (2.43)

n в правой части (2.43) – это число однородных пар вида (X_i, X_i), i = 1, 2, …, n. В силу равенств (2.42), (2.43) имеем

. (2.44)

Найдем через априорные вероятности классов ₁, ₂, …, _k.

_i  0, . (2.45)

Вероятность того, что произвольная пара точек (X_i, X_j) однородна и обе точки Х_i, Х_j принадлежат одному какому-то классу _s, s {1,2,…, k}, равна _s². Тогда вероятность того, что произвольная пара точек (Х_i, Х_j) однородна, равна . Функция

обладает тем свойством, что ее минимум при условиях (2.45) равен 1/k и достигается в точке [12]

₁ = ₂ = … = _k = ,

.

Тогда имеем

(2.46)

На основании соотношений (2.44), (2.46) получим

,

или в целочисленном виде

, (2.47)

где  – некоторое малое положительное число, E[Y] – целая часть Y.

Неравенства (2.41), (2.47) оценивают число классов снизу. Дадим для числа k оценку сверху через число инвариантных пар [12].

Определение 2.5. Пара точек (Х_i0, Х_j0) инвариантна, если каждая из них является ближайшей соседней точкой для другой.

,

.

Каждое множество точек имеет хотя бы одну инвариантную пару. Например, в множестве X⁽ⁿ⁾ инвариантной является та пара точек, расстояние между которыми равно r₍₁₎, r₍₁₎ – первый член ОВР этого множества. Каждый класс _S  X⁽ⁿ⁾, s = 1, 2, …, k, имеет хотя бы одну инвариантную пару точек. Если n_inv– число инвариантных пар множества X⁽ⁿ⁾, то для числа его классов k имеем

k < n_inv. (2.48)

Эксперименты показали, что каждый класс имеет не менее одной инвариантной пары точек и число инвариантных пар n_inv растет с увеличением элементов n множества X⁽ⁿ⁾, составляя от него 25–30%. Так что оценка (2.48) удобна лишь при небольших значениях n, n  30.

Отметим, что оценки для числа классов (2.41), (2.47), (2.48) можно использовать и в одномерном случае, если на данном множестве (2.32) предварительно задать подходящую метрику и построить гистограмму его ОВР.

8.4. Обнаружение классов с резко различающимися

плотностями точек

Локальные минимумы гистограммы ОВР могут порождаться существованием в множестве X⁽ⁿ⁾ как классов, далеко отстоящих друг от друга, так и классов с резко различающимися плотностями точек (РРПТ). Поэтому для корректного использования оценок для (2.41), (2.47) необходимо разделить множество X⁽ⁿ⁾ на такие подмножества, в которых классы имеют статистически равные плотности точек.

Для обнаружения классов с резко различающимися плотностями точек строится вариационный ряд минимальных расстояний. Минимальное расстояние от точки Х_i – это расстояние от Х_i до ее ближайшей соседней точки,

.

Определение 2.6. Вариационный ряд минимальных расстояний ВР_min – это упорядоченное по возрастанию множество минимальных расстояний {r_{i min}}, i=1, 2 , …, n,

.

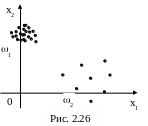
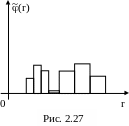
Для обнаружения классов с РРПТ при больших значениях n (n  30) строится гистограмма ВР_min. Если на этой гистограмме наблюдается хотя бы один СЗЛМ или «длинный хвост», то множество X⁽ⁿ⁾ содержит классы с РРПТ (рис. 2.27, 2.24).

Обнаружить классы с РРПТ можно и другим способом, применимым и для малых значениях n. Рассматривается последовательность отношений

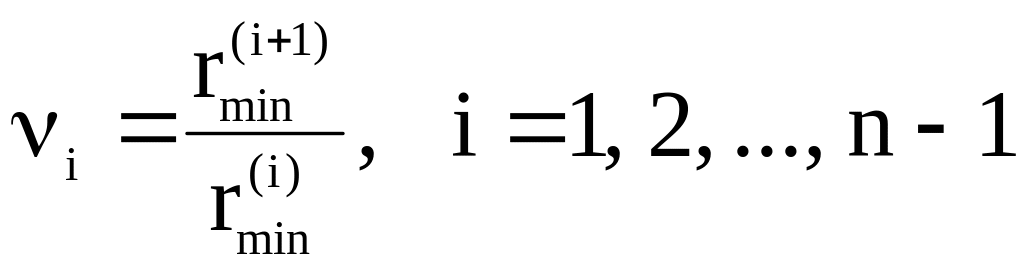. (2.48)

Если в последовательности (2.48) есть элементы, удовлетворяющие соотношению

, i = 1, 2, ..., n – 1, (2.49)

то множество Х⁽ⁿ⁾ содержит классы в РРПТ. Если неравенство (2.49) выполняется  раз, то множество Х⁽ⁿ⁾ имеет не менее  + 1 классов с РРПТ,

k   + 1.

В этом случае для дальнейшего исследования структуры множества Х⁽ⁿ⁾ его необходимо разделить на  + 1 подмножеств с почти равными плотностями точек. Каждое из этих подмножеств может быть объединением классов.