§ 5. Алгоритмы классификации в режиме с обучением

Задача классификации в режиме с обучением уже была сформулирована: имеется k классов

k , (2.8)

описанных своими основными признаками, новый объект X нужно отнести к одному из имеющихся классов. Дадим описание нескольких алгоритмов, по которым проводится классификация в этом режиме.

5.1. Алгоритм классификации по расстоянию

Для простоты и наглядности рассмотрим случай p = 2, k = 2. Пусть классы ₁, ₂ представлены своими обучающими выборками

(2.9)

n ₁ – число наблюдений класса ₁ , n₂ – число наблюдений класса ₂. Новое наблюдение X нужно отнести только к одному классу ₁ или ₂. На

рис. 2.5 представлена описанная ситуация.

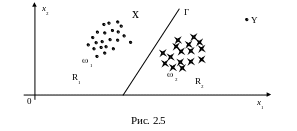
Зададим на множестве Хⁿ X⁽ⁿ⁾ = расстояние r(X_i , X_j), X_i , X_j X⁽ⁿ⁾ , n=n₁+n₂, и вычислим среднее расстояние от испытуемой точки X до всех точек каждого класса:

,

.

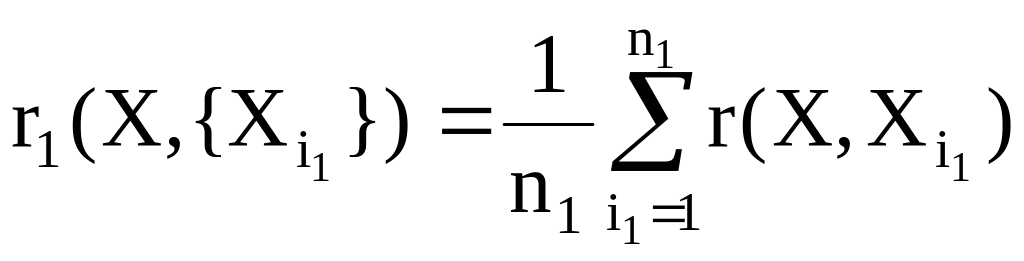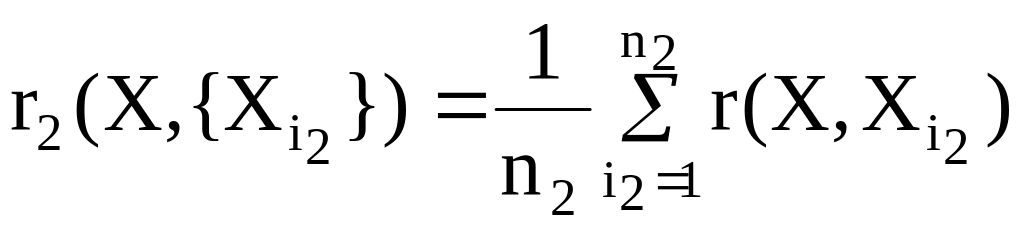Если имеем

r₁ < r₂ , (2.10 a)

то наблюдаемая точка X относится к классу ₁. Если

r₂ < r₁ , (2.10 b)

то точка Х относится к ₂. Если

r₂ = r₁ , (2.11)

то точку X можно отнести к любому из имеющихся классов. Уравнение (2.11) есть уравнение границы классов Г. Граница Г делит пространство признаков R на два подпространства R₁ и R₂ , которые содержат классы,

, .

Так что, если испытуемая точка X попадает в область R₁ (R₂), то естественно считать, что она принадлежит классу ₁ (₂).

Замечание. Если для испытуемой точки Y (рис. 2.5) имеет место одно из соотношений (2.10), (2.11) но значения r₁ и r₂ очень велики, например больше минимального диаметра классов d₁ , d₂

min(r₁ , r₂)  min(d₁ , d₂),

то не следует относить ее к одному из данных классов [6]. В этом случае правильным является решение: точка Y представляет новый класс ₃ . Поэтому для принятия правильного решения по соотношениям (2.10), (2.11) вводится порог r_пор для значений r₁ , r₂ ,

min(r₁ , r₂) r_пор ,

Например, можно положить

r_пор =   min(d₁ , d₂), 0,5 <  < 1.

5.2. Корреляционный алгоритм

Этот метод состоит в определении корреляции рассматриваемого объекта с каждым из эталонов, представляющих классы. Эталоны – векторы средних значений элементов каждого класса. Решающее правило: объект X относится к тому классу, для которого коэффициент корреляции наибольший.

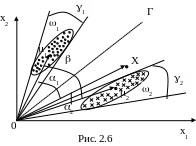
Классы _1, ₂ представлены своими обучающими выборками (2.9), изображенными на рис. 2.6.

Эталоны классов _1, ₂ — их средние значения определяются по формулам

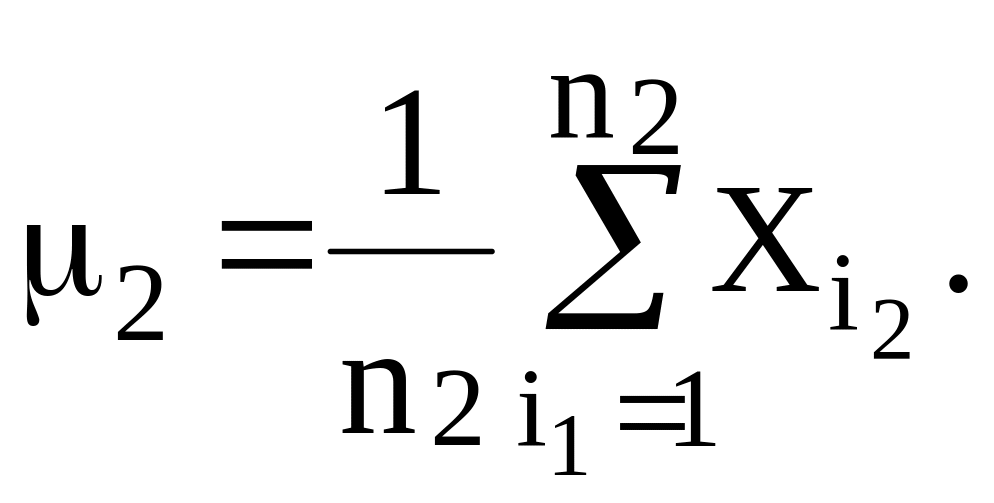
Корреляция объектов–векторов определяется косинусом угла между ними. Косинус угла между векторами находится из их скалярного произведения:

Отсюда имеем

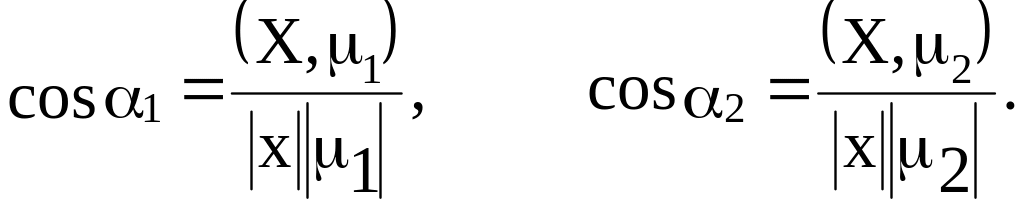(2.12)

Скалярное произведение векторов

и их модули выражаются через их координаты:

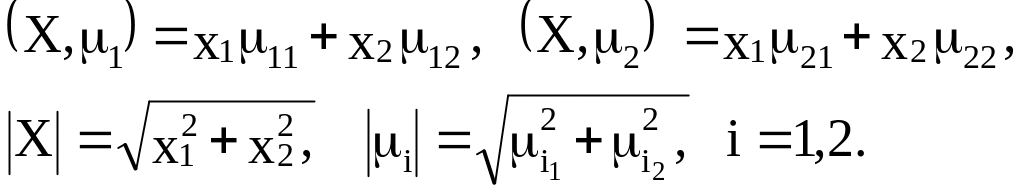
Вычислив по формулам (2.12), переходят к их сравнению. Если , то элемент X относится к классу ₁. Если , то элемент X относится к классу ₂ (рис. 2.6). Если

, (2.13)

то элемент X можно отнести к любому из классов ₁, _2. Уравне –

ние (2.13) - уравнение границы классов Г.

Решения, получаемые с помощью корреляционного метода, базируются на угловой близости точек X, μ₁, μ₂. Метод полезен, если каждый из углов ₁, ₂, охватывающий подмножества наблюдений из одного класса, мал по сравнению с углом между эталонами  (рис. 2.6),

(2.14)

Но если хотя бы одно из соотношений (2.14) не выполняется, то корреляционный метод неприменим, он может дать большие ошибки, так как часть точек из класса ₁ будет отнесена к классу ₂ (рис.2.7).

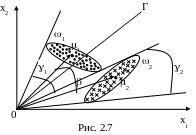
Корреляционный метод часто применяют при распознании букв машинописного текста.

5.3. Регрессионный алгоритм

Регрессионный алгоритм (РА) применяется в случае, когда обучающие выборки классов (2.9) сосредоточены вдоль некоторых линий, называемых линиями регрессий (рис. 2.3, 2.8). Если линии регрессий являются прямыми (рис. 2.8), то зависимость между координатами каждой точки из одного класса (₁ и ₂) можно представить в виде

где _i –– отклонение ординаты точки от ординаты точки . Аналогично _j –– отклонение ординаты точки от ординаты точки (рис. 2.8).

Каждая прямая регрессии ( , ) проходит через средние точки соответствующего класса. Из уравнений (2.15) имеем

Рис. 2.8

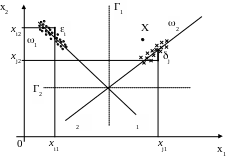
Неизвестные коэффициенты a, b и c, d в системах (2.16) определяются методом наименьших квадратов (МНК), минимизирующим сумму квадратов отклонений от каждой прямой регрессии [4, 8, 9].

Для системы уравнений (2.16a) имеем

. (2.17a)

Для удобства введем обозначение:

. (2.17б)

Минимум функции находится из необходимых условий ее экстремума:

, .

Продифференцировав функцию по a и b и приравняв полученные выражения частных производных к нулю, после простых алгебраических операций получим систему нормальных уравнений

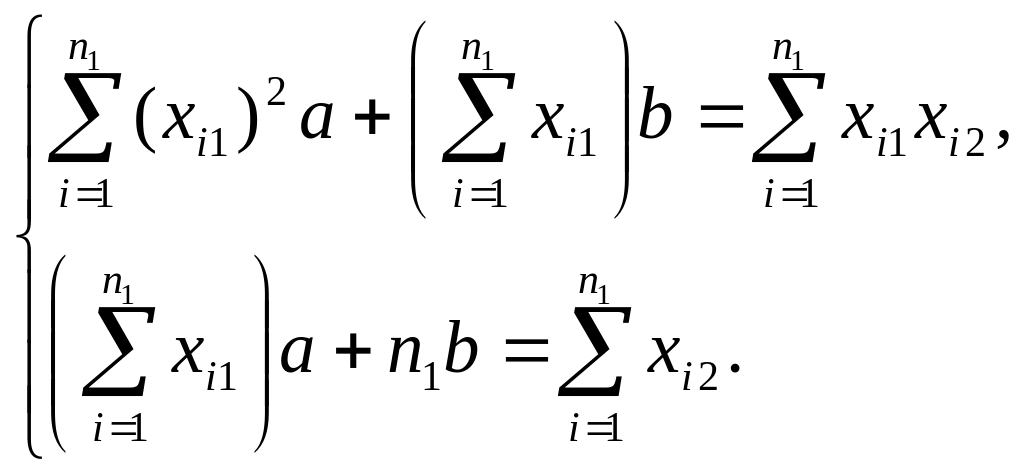(2.18)

Из системы (2.18) легко находятся оценки параметров a и b, являющиеся функциями наблюдений:

, .

Доказано, что при значениях a и b, определяемых из уравнений (2.18), функция (2.17) имеет минимум [7].

Аналогично методом наименьших квадратов из уравнений (2.16б) оцениваются значения параметров с, d.

Таким образом, получаются уравнения линий регрессий, описывающих классы ₁ и ₂,

_,

Поиск уравнения регрессии для каждого класса относится к процессу обучения. Чтобы отнести испытуемое наблюдение X к одному из имеющихся классов, необходимо вычислить расстояния от точки X до линий регрессий и , r(x, ), r(x, ) соответственно.

Если r(X, ) < r(X, ), то Х относится к классу ₁.

Если r(X, ) < r(X, ), то X относится к классу ₂.

Если

r(X, ) = r(X, ), (2.19)

то X можно отнести к любому из классов ₁, ₂. Уравнение (2.19) – уравнение границы классов ₁, ₂, уравнение биссектрис углов между прямыми и . Если линии регрессии и параллельны, то границей классов ₁, ₂ является прямая Г, параллельная прямым , и равноудаленная от них.

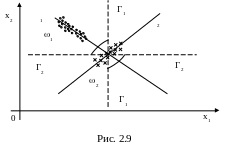
Регрессионный алгоритм неприменим, если один из классов попадает в точку пересечения линий регрессии (рис. 2.9). В этом случае РА дает большую ошибку, значительная часть точек класса ₂ по правилу классификации относится к классу ₁.

При в случае линейной регрессии имеем систему уравнений:

, i = 1, 2, …, n₁ .

Оценки для неизвестных параметров a₁, a₂, …, a_p находятся методом наименьших квадратов.

Одна из основных задач регрессионного анализа – задание уравнения регрессии

, ,

наиболее согласующегося с исходными наблюдениями (2.9). Проверка такой согласованности проводится по статистическим критериям [8].

В научно-практических исследованиях широко используются такие виды регрессий, как полиномиальные, экспоненциальные, логарифмические, тригонометрические и др.