
- •Н.Н. Апраушева элементарный курс
- •Решений
- •Научное издание
- •Н.С. Гумилев
- •Глава 1. Элементы теории эвристических решений (эр)
- •§1. Строгие и эвристические методы пр
- •§2. Общая структура процесса принятия решения
- •§3. Центральная проблема теории эр
- •§4. Краткая история развития эр
- •Глава 2. Принятие решений в распознавании образов
- •§ 1. Понятие о распознавании образов, классификации
- •§2. Условия применимости математических
- •§3. Критерий оптимальной классификации
- •§4. Основные условия, гарантирующие оптимальную
- •§ 5. Алгоритмы классификации в режиме с обучением
- •§6. Классификация как задача статистической
- •§7. Алгоритмы автоматической классификации (ак)
- •§8. Предварительное обнаружение классов
- •Глава 3. Общая математическая теория принятия решений
- •§1. Принятие решений в условиях неопределенности
- •§ 2. Принятие решений в условиях риска
- •§3. Принятие решений при проведении эксперимента
- •§4. Принятие решений при проведении
- •Ррпт – резко различающиеся плотности точек,
§ 2. Принятие решений в условиях риска
Ситуация ПР в условиях риска возникает в случаях, когда известны априорные вероятности состояний природы
р(Q1), р(Q2), … , р(Qn),
 . (3.5)
. (3.5)
Естественно воспользоваться этой дополнительной информацией. С этой целью для каждой операции аi находят взвешенные суммы полезностей
 i=1,2, …, m ,
(3.6)
i=1,2, …, m ,
(3.6)
и выбирают в
качестве наилучшей ту операцию
![]() ,
для которой взвешенная сумма
полезностей в (3.6) максимальна,
,
для которой взвешенная сумма
полезностей в (3.6) максимальна,
![]()
Пусть в рассмотренном выше примере р(Q1)=0.25, р(Q2)=0.75. По данным табл. 3.3 имеем
![]() =
10.25
+ 110.75
= 8.5,
=
10.25
+ 110.75
= 8.5,
![]() =
100.25
+ 60.75
= 7.0,
=
100.25
+ 60.75
= 7.0,
![]() =
00.25
+ 140.75
= 10.5,
=
00.25
+ 140.75
= 10.5,
max (8.5; 7.0; 10.5) = 10.5.
Следовательно, наилучшей операцией является операция а3, если р(Q1)=0.25, р(Q2)=0.75. Но при других значениях априорных вероятностей состояний природы возможен и другой выбор. Используя данные табл.3.3 и формулу (3.6) для каждой операции аi, i = 1,2,3, имеем
![]() =
р +11(1 –
p)
= 11 – 10p,
=
р +11(1 –
p)
= 11 – 10p,
![]() =
10p
+6(1 – p)
= 6 + 4p,
=
10p
+6(1 – p)
= 6 + 4p,
![]() =
14(1 – p)
= 14 – 14p.
=
14(1 – p)
= 14 – 14p.
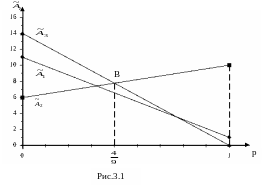
На рис.3.1 даны
графики функций
![]() ,
i = 1, 2, 3.
,
i = 1, 2, 3.
р
Рис.3.1
В

![]()

![]()

![]()
![]()
![]()
Прямые
,
пересекаются в точке В, при
![]() ,
вычисленном из равенства 6 + 4р = 14 – 14р.
Из рис. 3.1 следует, что при
,
вычисленном из равенства 6 + 4р = 14 – 14р.
Из рис. 3.1 следует, что при
![]() лучшей операцией является а3,
а при
лучшей операцией является а3,
а при
![]() лучшей операцией является а2.
При
лучшей операцией является а2.
При
![]() безразлично, какую операцию а2 или
а3 использовать. Операцию а1
применять невыгодно.
безразлично, какую операцию а2 или
а3 использовать. Операцию а1
применять невыгодно.
Если р=0 или 1, то имеем ситуацию ПР в условиях достоверности. При р=0 лучшая операция – а3, при р=1 лучшая операция – а2.
§3. Принятие решений при проведении эксперимента
3.1. Принятие решений в условиях неопределенности
Человек, прежде чем принять решение, пытается получить некоторую информацию о состоянии природы экспериментальным путем. Предполагается, что проведение эксперимента не требует никаких затрат,
Пусть проведен эксперимент, имеющий t исходов – возможных прогнозов состояния природы,
Z=(z1,
z2,…,
zt),
![]() .
.
Известна условная вероятность Р(zβ/Qj) -го результата эксперимента при состоянии природы Qj,
Pj= Р(zβ/Qj), =1,2,…,t, j=1,2,…,n. (3.7)
Множество значений Pj можно представить в виде матрицы размера t·n, данной в табл. 3.5.
Для использования информации, полученной в результате эксперимента, введем понятие стратегии.
Таблица 3.5
Z |
Q1 |
Q2 |
… |
Qn |
z1 |
P11 |
P12 |
… |
P1n |
z2 |
P21 |
P22 |
… |
P2n |
… |
… |
… |
… |
… |
zt |
Pt1 |
Pt2 |
… |
Ptn |
Определение 3.2. Стратегия - это соответствие последовательности t результатов эксперимента последовательности t операций,
(z1, z2,…, zt)→ (ai, aj,…, ak). (3.8)
Выражение (3.8) подразумевает, что
z1→
ai,
![]() ,
,
z2→
aj,
![]() ,
,
……………………
zt→
ak,
![]() .
.
Число возможных стратегий определяется формулой
= mt,
m – число операций, t - число результатов эксперимента. При m=2, t=3 всевозможные стратегии представлены в табл.3.6.
Таблица 3.6
-
 Si
Siz
S1
S2
S3
S4
S5
S6
S7
S8
z1
a1
a1
a1
a1
а2
а2
а2
а2
z2
a1
a1
а2
а2
a1
a1
а2
а2
z3
a1
а2
a1
а2
a1
а2
a1
а2
Задача ПР формулируется так: какую одну из операций a1,a2,…, am следует выбрать в зависимости от одного из результатов эксперимента z1, z2,…, zt.
Для принятия решения находим усредненные полезности стратегий Si, i= 1,2, …, , при состояниях природы Qj, j=1, 2, …, n,
U(Si,Qj)=![]() αi
β
j Pβ
j
, i= 1,2, …, ,
j=1, 2, …, n, (3.9)
αi
β
j Pβ
j
, i= 1,2, …, ,
j=1, 2, …, n, (3.9)
где αiβj - полезность β-й компоненты i-й стратегии при состоянии природы Qj, Pβj – условная вероятность β-го результата эксперимента при состоянии природы Qj. Стратегия Si определена множеством операций, значения αi β j берутся из таблицы полезностей значения Pβj – из табл. 3.5. Полученные значения усредненных полезностей U(Si,Qj) можно записать в виде матрицы размера n·. Для принятия решения – выбора наилучшей стратегии можно воспользоваться уже рассмотренными критериями: максимина, минимакса сожалений и равновозможных состояний.
Рассмотрим конкретный пример. Предполагаются лишь два состояния природы: Q1 - теплая погода, Q2 – холодная погода,
и - только две
операции:
![]() –
одеться для теплой погоды,
–
одеться для теплой погоды,
![]() –одеться
для холодной погоды. Эта ситуация
характерна для туристов. Матрица
полезности дана в табл.3.7.
–одеться
для холодной погоды. Эта ситуация
характерна для туристов. Матрица
полезности дана в табл.3.7.
Таблица 3.7 Таблица 3.8
-
 Qj
Qjai
Q1
Q2
Qj
z
Q1
Q2
a1
10
0
z1
0.6
0.3
z2
0.2
0.5
a2
4
7
z3
0.2
0.2
Критерий максимина гарантирует 4 ед. полезности и рекомендует выбирать операцию а2. Критерий минимакса дает этот же ответ.
Но есть возможность воспользоваться данными прогноза погоды (в этом и состоит эксперимент), которые могут быть трех видов:
z1 – ожидается теплая погода,
z2 – ожидается холодная погода,
z3 – прогноз неизвестен.
Из прошлого опыта
известны условные вероятности этих
трех видов прогноза для каждого состояния
природы
![]() ,
=1,2,3, j
=1,2, представленные в табл. 3.8.
,
=1,2,3, j
=1,2, представленные в табл. 3.8.
Для каждой из 8 стратегий и каждого из 2–х состояний природы определим взвешенные суммы полезностей по формуле (3.9), используя данные табл. 3.6 – 3.8,
U(S1,Q1) =100.6 + 100.2 +100.2 =10,
U(S2,Q1) =100.6 + 100.2 +40.2 = 8.8,
U(S3,Q1) =100.6 + 40.2 + 100.2 = 8.8,
........................................................
U(S8,Q1) = 40.6 + 40.2 + 40.2 = 4,
U(S1,Q2) = 00.3 + 00.5 +00.2 = 0,
.........................................................
U(S8,Q2) = 70.3 + 70.5 + 70.2 = 7.
Все вычисленные значения U(Si,Qj), i = 1,2,…8, j = 1, 2, помещены в табл.3.9, [13].
Таблица 3.9
Qj |
S1 |
_ S2 |
S3 |
S4 |
_ S5 |
_ S6 |
S7 |
S8 |
Q1 |
10 |
8.8 |
8.8 |
7.6 |
6.4 |
5.2 |
5.2 |
4 |
Q2 |
0 |
1.4 |
3.5 |
4.9 |
2.1 |
3.5 |
5.6 |
7 |
Из табл. 3.9
предварительно следует исключить
плохие стратегии – те стратегии,
обе компоненты которых не больше ()
соответствующих компонент какой–либо
другой стратегии. Ввиду того, что
![]() ,
,
![]() ,
S6 ≤ S7,
стратегии
,
S6 ≤ S7,
стратегии
![]() исключаются из рассмотрения (в табл.
3.9 они помечены знаком "–").
исключаются из рассмотрения (в табл.
3.9 они помечены знаком "–").
К оставшимся
допустимым стратегиям
![]() можно применить известные нам критерии.
Используя критерий максимина, имеем
можно применить известные нам критерии.
Используя критерий максимина, имеем
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Следовательно,
наилучшей стратегией является стратегия
S7, гарантирующая
5.2 ед. полезности. Для сравнения
максиминная операция
![]() гарантирует лишь 4 ед. полезности. Так
как S7 = (a2,
a2, a1),
то в силу (3.8) имеем
гарантирует лишь 4 ед. полезности. Так
как S7 = (a2,
a2, a1),
то в силу (3.8) имеем
![]() .
.
Это значит, что при прогнозе z1 выбирается операция а2, при прогнозе z2 – a2, при прогнозе z3 – a1, т.е. максиминная стратегия S7 рекомендует одеваться тепло, если прогноз – теплая или холодная погода, и одеваться легко, если прогноз неизвестен. Последнее утверждение весьма непрактично.
Максиминная
стратегия S7 при
неблагоприятном стечении обстоятельств
может привести и к худшему результату,
чем максиминная операция
.
Например, имеет место холодная погода
![]() .
Тогда согласно максиминной операции
турист получит 7 ед. полезности (табл.
3.7). С другой стороны, если результат
прогноза будет
.
Тогда согласно максиминной операции
турист получит 7 ед. полезности (табл.
3.7). С другой стороны, если результат
прогноза будет
![]() (прогноз
неизвестен) и согласно стратегии S7
будет выбрана операция
(прогноз
неизвестен) и согласно стратегии S7
будет выбрана операция
![]() (одеться легко),то он получит 0 ед.
полезности. Это явление –– типичное
для теории игр и теории принятия решений.
S7 гарантирует лишь
среднюю полезность в 5.2 ед.
(одеться легко),то он получит 0 ед.
полезности. Это явление –– типичное
для теории игр и теории принятия решений.
S7 гарантирует лишь
среднюю полезность в 5.2 ед.
3.2. Использование смешанной стратегии
Определение 3.3. Стратегия S* называется смешанной, если она представлена в виде выпуклой комбинации двух других стратегий,
S* = сSm1 + (1 - с)Sm2, 0<с<1, m1, m2 {1, 2, …, t}.
Это определение базируется на понятии выпуклой комбинации точек [14]. Переход к смешанной стратегии осуществляется с целью повышения гарантированной средней полезности.
Стратегии
рассмотренного выше примера изобразим
точками на п лоскости
с координатами
лоскости
с координатами
![]() ,
,
![]() ,
i=1,3,4,7,8 (рис. 3.2).
,
i=1,3,4,7,8 (рис. 3.2).
По рис. 3.2 видно,
что если взять в определенных пропорциях
стратегии S4 и S8,
то получим смешанную стратегию, лучшую
по сравнению со стратегией S7.
Проведем биссектрису I
координатного угла и найдем точку
пересечения ее с отрезком [S4,
S8] –– точку
![]() .
.
Запишем уравнение прямой, проходящей через две точки: S4(7.6; 4.9), S8 (4;7) [15],
 ,
,
которое приводится к виду
![]() .
.
Из этого уравнения
находим координаты точки
,
для которой
![]() ,
,
![]() .
.
Так как
![]() ,
то стратегия
лучше стратегии S7,
гарантирующей 5.2 ед. полезности, S*>S7.
,
то стратегия
лучше стратегии S7,
гарантирующей 5.2 ед. полезности, S*>S7.
Теперь остается представить стратегию в виде выпуклой комбинации стратегий S4, S8,
S* = cS4 + (1 – c)S8, 0 < c <1. (3.10)
Для определения значения параметра c достаточно записать уравнение (3.10) для абсцисс входящих в него точек
![]()
из которого
получаем
![]() .
Тогда равенство (3.10) принимает вид
.
Тогда равенство (3.10) принимает вид
![]() .
(3.11)
.
(3.11)
Так как
![]() ,
,
![]() ,
то в силу равенства (3.11) имеем
,
то в силу равенства (3.11) имеем
![]() .
.
Практически смешанную стратегию S* можно реализовать так. Если результат эксперимента есть z2 или z3, то используется операция a2.
Если же результат
эксперимента есть z1,
то с помощью подходящего случайного
механизма с вероятностью
![]() используется операция a1
и с вероятностью
используется операция a1
и с вероятностью
![]() –– операция а2. Основой случайного
механизма могут служить 19 одинаковых
карточек, на 10 из которых записан символ
а1, а на 9 –– символ а2. Из
этого набора 19 карточек случайно
выбирается одна, и используется та
операция, символ, которой изображен на
этой карточке.
–– операция а2. Основой случайного
механизма могут служить 19 одинаковых
карточек, на 10 из которых записан символ
а1, а на 9 –– символ а2. Из
этого набора 19 карточек случайно
выбирается одна, и используется та
операция, символ, которой изображен на
этой карточке.
3.3. Принятие решений в условиях риска
К условиям, перечисленным в п. 3.1, добавляется еще одно – значения априорных вероятностей состояний окружающей среды (природы):
p(Q1), p(Q2), ..., p(Qn). (3.12)
Тогда для каждой
стратегии
![]() определяется усредненная по всем
состояниям природы средняя полезность
определяется усредненная по всем
состояниям природы средняя полезность
![]() по формуле
по формуле
![]() ,
(3.13)
,
(3.13)
U(Si,Qj)
– полезность стратегии
![]() при состоянии природы
при состоянии природы
![]() ,
которая находится по формуле (3.9). Затем
из множества
,
которая находится по формуле (3.9). Затем
из множества
![]() ,
,
![]() ,
выделяется максимальный элемент,
,
выделяется максимальный элемент,
![]() ,
,
![]() .
.
Определение
3.4. Стратегия
![]() ,
обладающая максимальной средней
полезностью
,
обладающая максимальной средней
полезностью
![]() ,
называется байесовской стратегией,
,
называется байесовской стратегией,
![]() ,
.
,
.
Пусть в рассмотренном ранее примере р(Q1) = 0.6, p(Q2) = 0.4. Используя данные табл. 3.9 и формулу (3.13), вычислим среднюю полезность для каждой допустимой стратегии,
![]() =
100.6
+ 00.4
= 6,
=
100.6
+ 00.4
= 6,
![]() =
8.80.6
+ 3.50.4
= 6.68,
=
8.80.6
+ 3.50.4
= 6.68,
![]() =
7.60.6
+ 4.90.4
= 6.52,
=
7.60.6
+ 4.90.4
= 6.52,
![]() =
5.20.6
+5.60.4
=5.36,
=
5.20.6
+5.60.4
=5.36,
![]() =
40.6
+ 70.4
=5.2 .
=
40.6
+ 70.4
=5.2 .
Затем найдем наибольшее число из полученных пяти чисел,
![]()
Следовательно,
оптимальной стратегией является
стратегия
![]() ,
обладающая максимальной средней
полезностью, равной 6.68 ед.
,
обладающая максимальной средней
полезностью, равной 6.68 ед.
Заметим, что
стратегия
является байесовской для конкретных
значений априорных вероятностей: р(Q1)
= 0.6, p(Q2)
= 0.4. При других значениях р(Q1),
р(Q2) байесовской
может быть и другая стратегия. Так, при
р(Q1) = 0.5, p(Q2)
= 0.5 байесовской является стратегия
![]() .
.
Проведение эксперимента в рассмотренной ситуации выгодно. Действительно, если эксперимент не проводить, то по данным табл. 3.7 имеем
![]()
Байесовской операцией (стратегией) является операция а1, средняя полезность которой равна 6 ед.
Для дальнейших рассуждений нам понадобится объединить выражения (3.13), (3.9) в одно,
![]() .
.
Меняя порядок суммирования в правой части последнего равенства, получим
![]() (3.14)
(3.14)
Из
этого равенства следует, что при выборе
оптимальной стратегии
![]() максимизация
сводится к максимизации выражения в
квадратных скобках в правой части
(3.14), т.е. для каждого результата
эксперимента zβ
максимизация полезности Uβ(ai)
сводится к выбору такой операции
максимизация
сводится к максимизации выражения в
квадратных скобках в правой части
(3.14), т.е. для каждого результата
эксперимента zβ
максимизация полезности Uβ(ai)
сводится к выбору такой операции
![]() ,
которая максимизирует выражение в
квадратных скобках.
,
которая максимизирует выражение в
квадратных скобках.
3.4. Использование формулы Байеса
В общем случае число допустимых стратегий Si, i = 1, 2,…, , может быть очень велико, и поэтому пользоваться формулой (3.13) затруднительно. Эта трудность обходится с помощью формулы Байеса [3, 8, 13]. Проводя эксперимент, оценивают новые апостериорные вероятности состояний природы P(Qj/z), j = 1, 2, …, n, = 1, 2, …, t. Используя эти уточненные вероятности состояний природы, находят оптимальную операцию ai, i {1, 2, …, m}, обычным способом. Для простоты предположим, что распределения дискретные. Согласно формуле Байеса для апостериорной вероятности состояния природы Qj при результате эксперимента z имеем
![]() ,
j=
1, 2,…,n,
=1, 2,…, t,
(3.15)
,
j=
1, 2,…,n,
=1, 2,…, t,
(3.15)
![]() –
известная условная
вероятность получить результат
эксперимента z
при состоянии природы Qj, p(Qj)
– априорная вероятность состояния
природы Qj, P(z)
– полная вероятность результата
эксперимен-та z
–
известная условная
вероятность получить результат
эксперимента z
при состоянии природы Qj, p(Qj)
– априорная вероятность состояния
природы Qj, P(z)
– полная вероятность результата
эксперимен-та z
![]() . (3.16)
. (3.16)
Фиксируя , {1, 2,…, t}, для каждой операции ai, i =1, 2, … ,m, находим среднюю полезность U (ai ) по формуле
![]() , (3.17)
, (3.17)
![]() – условная
вероятность, определяемая из равенства
(3.15), i
j – полезность
операции a i
при состоянии природы Qj.
Далее при фиксированном значении
находим
– условная
вероятность, определяемая из равенства
(3.15), i
j – полезность
операции a i
при состоянии природы Qj.
Далее при фиксированном значении
находим
![]() .
.
Операцию![]() ,
i
{1, 2,…, m},
считаем оптимальной для данного
результата эксперимента z,
{1,
2,…, t},
,
i
{1, 2,…, m},
считаем оптимальной для данного
результата эксперимента z,
{1,
2,…, t},
![]() .
.
Покажем, что таким путем получается байесовская стратегия
SB
=![]() .
.
В силу формул (3.15) – (3.17) имеем
 .
(3.18)
.
(3.18)
Из этого равенства следует, что для каждого результата эксперимента z максимизация полезности U(ai ) сводится к отысканию такой операции которая максимизирует выражение в квадратных скобках в его правой части
В формулах (3.14),
(3.18) для каждого результата эксперимента
максимизация![]() ,
U (ai)
сводится к нахождению такой операции
,
U (ai)
сводится к нахождению такой операции
![]() ,
которая максимизирует выражения в
квадратных скобках, стоящих в их правых
частях. А так как эти максимизирующие
операции совпадают, то оба метода
приводят к одному и тому же результату,
что и требовалось доказать.
,
которая максимизирует выражения в
квадратных скобках, стоящих в их правых
частях. А так как эти максимизирующие
операции совпадают, то оба метода
приводят к одному и тому же результату,
что и требовалось доказать.
Затем находится максимальная усредненная по всем результатам эксперимента средняя полезность по формуле
![]() i=1,2,…,m,
(3.19)
i=1,2,…,m,
(3.19)
где U(ai) определяется из равенства (3.17).
Отметим, что при отыскании оптимальной стратегии в вычислительном отношении проще использовать формулы (3.17), (3.15), а не формулы (3.13), (3.9).
В нашей задаче найдем оптимальную стратегию SB, используя второй метод, т.е. формулы (3.15) и (3.17).
Для = 1 находим U1(a1),U1(a2),
![]()
![]()
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
i
= 1, 2.
,
i
= 1, 2.
Следовательно, при z1 оптимальной операцией является а1, дающая 7.5 ед. полезности, P(z1) = 0.48.
Для =2 находим U2(a1), U2(a2),
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
i
= 1, 2.
,
i
= 1, 2.
Следовательно, при z2 оптимальной операцией является a2, дающая 5.875 ед. полезности, P(z2)=0.32.
Для =3 находим U3(a1), U3(a2),
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
,
![]() ,
i
= 1, 2.
,
i
= 1, 2.
Следовательно, при z3 оптимальной операцией является a1, дающая 6 ед. полезности, P(z3)=0.20.
Оптимальной, байесовской стратегией является стратегия
![]() ,
,
совпадающая со стратегией S3, полученной при использовании формул (3.9), (3. 13).
Вычислим максимальную (усредненную по трем результатам эксперимента) среднюю полезность по формуле (3.19),
![]() ,
,
что
совпадает со значением
![]() ,
полученным ранее.
,
полученным ранее.

 Qj
Qj
 Si
Si