30. Решение дифференциальных уравнений.

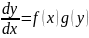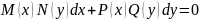1.Диф. ур. с разделяющимися переменными: диф. ур. I порядка называется ур-ем с разделяющимися переменными если оно м.б. представлено в виде: или . Где 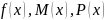– ф-и переменной x; 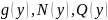– ф-и переменной y. Для решения ур-е следует преобразовать к виду в кот. дифференциал и ф-и переменной x окажутся в одной части рав-ва, а переменная y в другой. Затем обе части проинтегрировать: 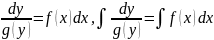. Находим интегр. и искомую ф-ю: 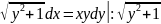, , 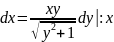. Выразим х. Для этого пропотенцируем: 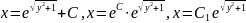. 2.Однородные диф. ур. I порядка: диф. ур-е I порядка назыв. однородным если оно м.б. представлено в виде: 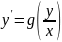, где g – некоторая ф-я одной перемен. Данное ур-е решается путём замены переменной 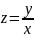, а затем сведение полученного ур-я к ур-ю с разделёнными переменными: 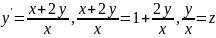– функция от перемен. x. 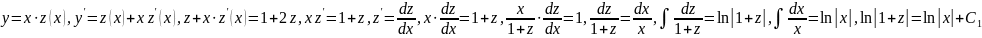. С₁ можно представить в виде ln C: 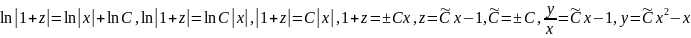. При решении данного ур-я следует учитывать, что 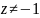. 3.Линейные диф. ур-я I порядка: это ур-е вида: 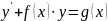. Где y(x)- непрерыв. ф-я перемен. х. Если 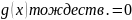, то ур-е однородн. Если 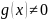, то ур. неоднородн. Реш-е м.б. найдено в виде 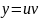: v – решение ур-я 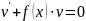, u – . 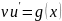Пример: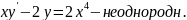 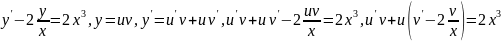функцию 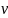подберём так, чтобы 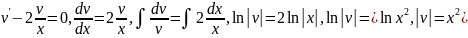(знак модуля можно опустить) => 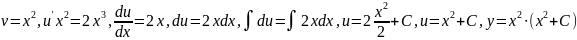. 4.Линенйные диф. ур-я II порядка с постоянным коэф.: это ур. вида: 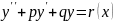. Где p,q – некот. действ. числа,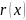 - нек-ая ф-я(если тождеств. =0, то ур-е однородн, в противном случае – неоднородн.). Решение:1) составим характерист. ур-е, кот. имеет вид: 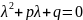(*). Находим реш-е 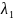и 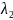и в зависимости от их знач-ий находим реш-е у соответствующего однород. Диф. ур-я: 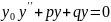. 2)находим некот. частн. реш-е неоднородн. Диф. ур-я, тогда общее реш-е записывается в виде суммы: 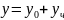(общее реш-е соотв. однород ур-я + частн. реш-е исходного неоднород. ур-я). Для общего реш-я однород. ур-я используется теорема: если характерист. ур-е имеет 2 различных действ. реш-я , то общее реш-е однородного ур-я имеет вид: 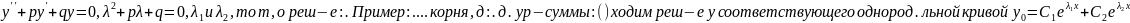. Если хар. Ур. имеет 2 одинак. действ. Корня, то реш-е: 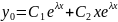. Пример: 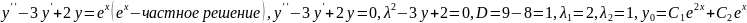. Для нахождения части реш-я, полагая что 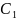и 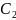- функции перемен. х, поэтому их следует определить. С этой целью продиф. Замечание: найти и можно методом вариации произв. пост. Суть метода: общее реш-е однородного ур-я можем представить в виде: 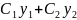. Ф-я зависит от х и продиф. Данное реш-е можно составить систему ур. из кот. могут быть получены и . 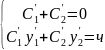. . 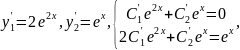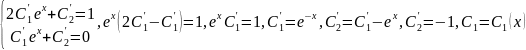. 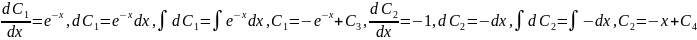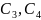- произв. числа. 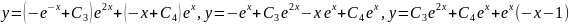.Замечание: первые 2 слаг. – общее решение соотв. однородного диф. ур., 3е слаг. – частное реш-е исходного ур-я (можно убедиться проверкой).