- •Понятие ф-и и способы ее задания
- •Функции в экономике
- •Вопрос 4. Числовая последовательность и ее пределы.
- •Вопрос 5. Предел функции, основные теоремы о пределах.
- •Вопрос 6. 1ый и 2ой замечательные пределы.
- •7.Бесконечно малые, бесконечно большие величины
- •8.Непрерывность функций. Точки разрыва, их классификация.
- •13. Производная и дифференциал высшего порядка.
- •14. Экономический смысл производной и понятие эластичности.
- •15. Приложение производной.
- •5.Теорема(правило) Лопиталя.
- •Вопрос 22 Экстремумы
- •Вопрос 23 Метод наименьших квадратов
- •24 Вопрос Неопределенный интеграл, свойства
- •25.Методы интегрирования неопред. Интеграла.
- •1. Непосредственное интегрирование.
- •2.Интегрирование по частям
- •3.Метод замены переменной
- •4.Интегрирование рациональных дробей.
- •27.Методы интегрирования определенноно интеграла.
- •28. Несобственные интегралы.
- •29. Дифференциальные уравнения.
- •30. Решение дифференциальных уравнений.
29. Дифференциальные уравнения.
Диф.
ур-е- это ур-е , связывающее искомую ф-ю
одной или нескольких переменных. Эти
перемен. и производные различных
порядков этой ф-и. В
общем виде диф. ур. м.б. представлено:
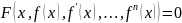 (1). Где f–некоторая
ф-я. Данная ф-я имеет n+2
перемен., где
(1). Где f–некоторая
ф-я. Данная ф-я имеет n+2
перемен., где
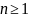 .
Порядок n
(порядок старшей произв.) называется
порядком ур-я. Замечание: если искомая
ф-я зависит от 1ой перемен., то диф. ур-е
называют обыкновенным. Если от нескольких
перем., то ур-е называется уравнением
в частных производных. Решением диф.
ур-я называется такая ф-я y=f(x)
при подстановке кот. в ур-е (1) обращает
его в тождество:
.
Порядок n
(порядок старшей произв.) называется
порядком ур-я. Замечание: если искомая
ф-я зависит от 1ой перемен., то диф. ур-е
называют обыкновенным. Если от нескольких
перем., то ур-е называется уравнением
в частных производных. Решением диф.
ур-я называется такая ф-я y=f(x)
при подстановке кот. в ур-е (1) обращает
его в тождество:
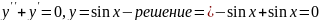 .
Если решение ур-я (1) получено в неявной
форме, т.е. F(x,y)=0,
то это ур-е называют интегралом диф.
ур-я. Задача о нахождении решения диф.
ур-я называется задачей интегрир-я
данного диф. ур-я. График решения диф.
ур-я называют интегр. кривой. Пусть
задано диф. ур-е (1). Общим решением
данного ур-я называется такое его реш-е:
.
Если решение ур-я (1) получено в неявной
форме, т.е. F(x,y)=0,
то это ур-е называют интегралом диф.
ур-я. Задача о нахождении решения диф.
ур-я называется задачей интегрир-я
данного диф. ур-я. График решения диф.
ур-я называют интегр. кривой. Пусть
задано диф. ур-е (1). Общим решением
данного ур-я называется такое его реш-е:
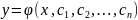 (2), кот. является ф-ей перемен. Х и
n-произвольных
независ. постоянных
(2), кот. является ф-ей перемен. Х и
n-произвольных
независ. постоянных
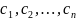 .
Если постоянным
придать вполне определённые значения,
то решение будем называть частным
реш-ем. Для нахождения частного реш-я
диф. ур-я в общем случае необходим задать
n-начальных
усл.
.
Если постоянным
придать вполне определённые значения,
то решение будем называть частным
реш-ем. Для нахождения частного реш-я
диф. ур-я в общем случае необходим задать
n-начальных
усл.
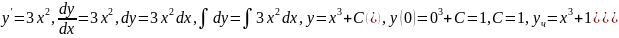 .
(*) – общее реш-е диф. ур-я, но если задать
условие, что при х0=0,
y=1,
то можно найти частное решение. (**) –
частное реш-е. Пример: из статистических
данных известно, что для некоторого
региона число умерших за ед. времени
пропорцианольно численности населения
соотв. c
коэф. k1,
k2.
Найти закон измениния численности
насел-я с течением времени. Решение:
пусть число жителей рег. В некоторый
момент времени t
определяется ф-ей:
.
(*) – общее реш-е диф. ур-я, но если задать
условие, что при х0=0,
y=1,
то можно найти частное решение. (**) –
частное реш-е. Пример: из статистических
данных известно, что для некоторого
региона число умерших за ед. времени
пропорцианольно численности населения
соотв. c
коэф. k1,
k2.
Найти закон измениния численности
насел-я с течением времени. Решение:
пусть число жителей рег. В некоторый
момент времени t
определяется ф-ей:
 .
.
Прирост
населения
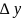 за время
за время
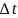 = разности между числом родившихся и
числом умерших за промежуток времени
.
= разности между числом родившихся и
числом умерших за промежуток времени
.
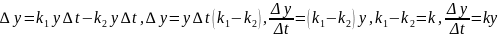 .
Устремив
к 0 в последнем рав-ве мы можем перейти
к lim:
.
Устремив
к 0 в последнем рав-ве мы можем перейти
к lim:
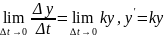 .
Мы получим диф. ур-е, а с другой стороны
мы получим мат. модель демографического
процесса. Решая данное ур-е мы получим
закон изменения численности населения:
.
Мы получим диф. ур-е, а с другой стороны
мы получим мат. модель демографического
процесса. Решая данное ур-е мы получим
закон изменения численности населения:
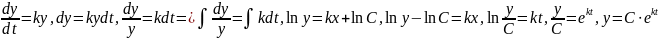 – решение ур-я и число жителей региона
в момент времени t.
C
– это const
определяемая нач. усл.(численность нас.
в нач. момент времен t).
Диф.
ур-я I
порядка.
Пусть задано диф. ур-е I
порядка:
– решение ур-я и число жителей региона
в момент времени t.
C
– это const
определяемая нач. усл.(численность нас.
в нач. момент времен t).
Диф.
ур-я I
порядка.
Пусть задано диф. ур-е I
порядка:
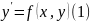 .
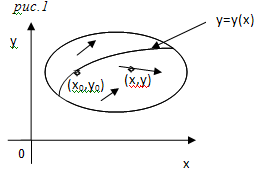
Рассмотрим геом. смысл данного диф.
ур-я. Он состоит в следующем: в каждой
точке плоскости XOY
направление касательной совпадает с
интегральной кривой y=y(x)б
проходящей через т. с координатами
(x,y)(рис.1).
Можно сказать, что ур-е (1) задаёт поле
направлений в некоторой области (гамма).
Решить ур-е (1) значит найти семейство
кривых, отвечающих данному полю
направлений. Теорема: пусть в диф. ур-е
(1) ф-я f(x,y)
и её частная произв.
.
Рассмотрим геом. смысл данного диф.
ур-я. Он состоит в следующем: в каждой
точке плоскости XOY
направление касательной совпадает с
интегральной кривой y=y(x)б
проходящей через т. с координатами
(x,y)(рис.1).
Можно сказать, что ур-е (1) задаёт поле
направлений в некоторой области (гамма).
Решить ур-е (1) значит найти семейство
кривых, отвечающих данному полю
направлений. Теорема: пусть в диф. ур-е
(1) ф-я f(x,y)
и её частная произв.
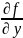 непрерыв. в открытом множ-ве Г координатной
плоскости XOY,
тогда: 1) для всякой т. (x0,
y0)
найдётся решение ур-я (1) удовл. Начальным
усл. y(x0)=y0.
2) если 2 реш-я ур-я (1)
непрерыв. в открытом множ-ве Г координатной
плоскости XOY,
тогда: 1) для всякой т. (x0,
y0)
найдётся решение ур-я (1) удовл. Начальным
усл. y(x0)=y0.
2) если 2 реш-я ур-я (1)
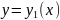 и
и
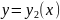 совпадают хотя бы для одного знач.
x=x0,
т.е.
совпадают хотя бы для одного знач.
x=x0,
т.е.
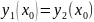 ,
то эти решения совпадают для всех x
для кот. определены. Геометрически
смысл теоремы состоит в том, что через
каждую точку с корд (x0,
y0)
мн-ва Г проходит одна и только одна
интегральная кривая ур-я (1). Задача
отыскания частного решения диф. ур-я
(1) удовл. нач. усл. y(x0)=y0
называется задачей Каши. Даная теорема
устанавливает усл. существов-я и
единственности реш-я задачи Каши.
,
то эти решения совпадают для всех x
для кот. определены. Геометрически
смысл теоремы состоит в том, что через
каждую точку с корд (x0,
y0)
мн-ва Г проходит одна и только одна
интегральная кривая ур-я (1). Задача
отыскания частного решения диф. ур-я
(1) удовл. нач. усл. y(x0)=y0
называется задачей Каши. Даная теорема
устанавливает усл. существов-я и
единственности реш-я задачи Каши.