
- •Понятие ф-и и способы ее задания
- •Функции в экономике
- •Вопрос 4. Числовая последовательность и ее пределы.
- •Вопрос 5. Предел функции, основные теоремы о пределах.
- •Вопрос 6. 1ый и 2ой замечательные пределы.
- •7.Бесконечно малые, бесконечно большие величины
- •8.Непрерывность функций. Точки разрыва, их классификация.
- •13. Производная и дифференциал высшего порядка.
- •14. Экономический смысл производной и понятие эластичности.
- •15. Приложение производной.
- •5.Теорема(правило) Лопиталя.
- •Вопрос 22 Экстремумы
- •Вопрос 23 Метод наименьших квадратов
- •24 Вопрос Неопределенный интеграл, свойства
- •25.Методы интегрирования неопред. Интеграла.
- •1. Непосредственное интегрирование.
- •2.Интегрирование по частям
- •3.Метод замены переменной
- •4.Интегрирование рациональных дробей.
- •27.Методы интегрирования определенноно интеграла.
- •28. Несобственные интегралы.
- •29. Дифференциальные уравнения.
- •30. Решение дифференциальных уравнений.
15. Приложение производной.
1.Теорема Ферма. Если дифференцируемая на [a,b] ф-ция у=f(х) достигает наибольшего (наименьшего) значения во внутр. точке этого промежутка, то в этой точке производная ф-ции =0. ( €[a,b], f’( )=0 )
2.Теорема Ролля. Пусть ф-ция у=f(х):
1) непрерывна на отрезке [a,b];
2) дифференцируема на интервале (a,b);
3) на концах отрезка принимает равные значения , f(a)=f(b),
Тогда внутри отрезка сущ-ет по крайней мере одна такая т.С, в кот-ой производная ф-ции = 0.
(Касательная к графику ф-ции в т.С II оси ОХ.)
3.Теорема Лагранжа. Пусть ф-ция у=f(х):
1) непрерывна на отрезке [a,b];
2) дифференцируема на интервале (a,b),
Тогда
внутри отрезка [a,b]
сущ-ет т.С такая, что производная в ней
равнна: f’(с)=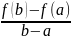 .
.
4.Теорема Каши. Пусть ф-ция у=f(х) и g(x):
1) непрерывны на отрезке [a,b];
2)
дифференцируемы на интервале (a,b);
причём 3)g’(x)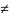 0
на (a,b),
0
на (a,b),
Тогда
внутри отрезка сущ-ет по крайней мере
одна т.С такая, что имеет место:
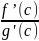 =
=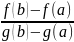 .
.
5.Теорема(правило) Лопиталя.
Предел
отношения 2х бесконечно больших или 2х
беск. малых ф-ций = пределу отношения
их производных, если последнее сущ-ет:
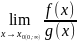 =
=
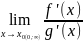 .
.
Данное
правило используют при раскрытии
неопределённости:
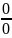 ;
;
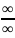 .
.
Замечание
1:
Это правило можно применить для раскрытия
неопределённости вида 0,
.
f(x)*g(x)
следует представить в виде :
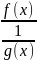 или
или
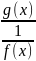 .
.
Замечание
2:
С помощью правила можно раскрывать
неопределённость вида
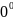 и
и
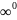 .
.
В
этом случае: :
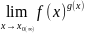 =
=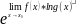 .
.
16.Использование
производной для исследования св-в
ф-ции. Пусть
задана ф-ция у=f(х)
непрерывная на (а,в) и дифф-ма на этом
промежутке. Будем говорить, что ф-ция
возрастает (убыв) на промежутке (а,в)
если её производная положительна
(отриц) во всех точках данногго промежутка.
Точкой х нулевое назыв точкой мах (мин)
если в некоторой малой окрестности
точки х нулевое выполняется неравенство:
f(х
нулевое) больше или равно f(х)
и наоборот. Если для всех точек х не
равно х нулевое этой окрестности
выполняется строгое неравенство f(х
нулевое) больше f(х)
и наоборот, то в этом случае говорят,
что х нулевое явл точкой строгого мах
или мин данной ф-ции. Необходимое
условие экстремума. В
точке экстремума ф-ции её производная
либо= 0 либо, не существует. Достаточное
условие экстремума.
1) если в точке х нулевое ф-ция у=f(х)
непрерывна, а производная f(х)
при переходе через точку х нулевое
меняет знак, то точка х нулевое явл
точкой экстремума, причем если знак
производной поменялся с + на – то точка
мах, если с – на + то точка х нулевое
мин. 2) если в точке х нулевое производная
f
штрих (х нулевое) =0, а вторая производная
положительна, то точка х нулевое явл
точкой мин. Если в точке х нулевое
производная fштрих
(х нулевое)=0. А вторая производная
отрицательна, о в точке х нулевое ф-ция
имеет мах.3) если у ф-ции у=f(х)
в точке х нулевое производная до порядка
n-1
включительно =0, а производна порядка
n
отлична от нуля в точке х нулевое, то
при n-нечет
экстремума нет, при n
–четн х нулевое явл точкой экстремума
при этом если n-ая
производная положительная, то х нулевое
точка мин, если отрицательно, то х
нулевое точа мах. Производную используют
для нахождения наибольшего или
наименьшего значения ф-ции на промежутке
(а,в). С этой целью для ф-ции у=f(х)
на (а,в) необходимо определить точки
экстремума, найто значения ф-ции на
концах отрезка (а,в) и точках экстремума
и из полученных значений выбрать
наименьшее и наибольшее.
Замечание.
Если
дифф-мая
на
интервале (а,в) ф-ция у=f(х)
имеет единственную точку экстремума,
то в этой точке достигается наибольшее
или наименьшее значение на интервале
(а,в). Интервалы
выпуклости ф-ции и точка перегиба. Ф-ция
у=f(х)
называется выпуклой вверх на промежутке
(а,в) если для любых 2-ух значений х1 и х2
из этого промежутка выполняется
неравенство f( ) ≤
) ≤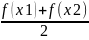 для
выпуклой ф-ции график ф-ции будет ниже
касательной. Для вогнутой график будет
выше касательной. Если 2-ая производная
f
штрих (х) ф-ции у=f(х)положительна
на промежутке (а,в), то на этом промежутке
ф-ция явл выпуклой вниз. Если 2-ая
производная f
два штриха (х) ф-ция у=f(х)
отрицательна на промежутке (а,в) то на
этом промежутке ф-ция выпукла вверх.
Если при переходе через точку х нулевое
меняется характер выпуклости, то точка
х нулевое назыв точкой перегиба т.е.
точка перегиба это точки разделяющие
интервалы выпуклости. Если точка х
нулевое точка перегиба ф-ции у=f(х),
то вторая производная ф-ции в этой точке
=0. Если вторая производная меняет знак
при переходе через точку х нулевое, то
точка х нулевое явл точкой перегиба
ф-ции у=f(х).
Асимптоты.
Прямая называется асимптотой графика
ф-ции у=f(х)
если расстояние от точки х1f(х)
до этой прямой стремится к 0при
неограниченном удалении графика от
начала координат. Различают 3 вида
асимптот: 1. Вертикальные. 2. Горизонтальные.
3. Наклонные. Прямая х=х0 назыв вертикальной
асимптотой
графика ф-ции у=f(х)
если хотя бы 1 из пределов слева и
справа=±∞ . х 0 точка разрыва или граничная
точка D(y),
тогда прямая будет вертикальна. Прямая
у=в нызыв горизонтальной
асимптотой
,если предел f(х)
х → ∞ = в. Прямая у=kx+b
назыв наклонной
асимптотой
к графику ф-ции у=kx+b,
если k-предел.
k=
предел f(х)/х,
х→ ∞, в= предел х→ ∞ (f(х)-k(х))
(k≠0).
для
выпуклой ф-ции график ф-ции будет ниже
касательной. Для вогнутой график будет
выше касательной. Если 2-ая производная
f
штрих (х) ф-ции у=f(х)положительна
на промежутке (а,в), то на этом промежутке
ф-ция явл выпуклой вниз. Если 2-ая
производная f
два штриха (х) ф-ция у=f(х)
отрицательна на промежутке (а,в) то на
этом промежутке ф-ция выпукла вверх.
Если при переходе через точку х нулевое
меняется характер выпуклости, то точка
х нулевое назыв точкой перегиба т.е.
точка перегиба это точки разделяющие
интервалы выпуклости. Если точка х
нулевое точка перегиба ф-ции у=f(х),
то вторая производная ф-ции в этой точке
=0. Если вторая производная меняет знак
при переходе через точку х нулевое, то
точка х нулевое явл точкой перегиба
ф-ции у=f(х).
Асимптоты.
Прямая называется асимптотой графика
ф-ции у=f(х)
если расстояние от точки х1f(х)
до этой прямой стремится к 0при
неограниченном удалении графика от
начала координат. Различают 3 вида
асимптот: 1. Вертикальные. 2. Горизонтальные.
3. Наклонные. Прямая х=х0 назыв вертикальной
асимптотой
графика ф-ции у=f(х)
если хотя бы 1 из пределов слева и
справа=±∞ . х 0 точка разрыва или граничная
точка D(y),
тогда прямая будет вертикальна. Прямая
у=в нызыв горизонтальной
асимптотой
,если предел f(х)
х → ∞ = в. Прямая у=kx+b
назыв наклонной
асимптотой
к графику ф-ции у=kx+b,
если k-предел.
k=
предел f(х)/х,
х→ ∞, в= предел х→ ∞ (f(х)-k(х))
(k≠0).
17. Полная схема исследования ф-ции и построение графика:1. Одз. 2. Определение четности. 3. Периодичность. 4. Экстремумы и характер монотонности. 5. Точки перегиба и характер выпуклости. 6. Асимптоты. 7. Точки пересечения с осями координат (если необходимо некоторые промежуточные значения).

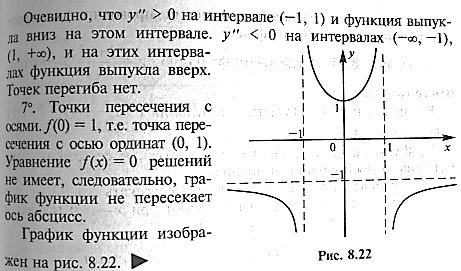
18. Функция нескольких переменных. Если каждому набору из n переменных: х1,х2,х3,…,хn из некоторого множества хn поставить в соответствие некоторое вполне определенное значение переменной Z, то говорят, что задана ф-ция нескольких переменных Z=f(х1,х2,…,хn). Множество х-область определения ф-ции. Множество которое принимает переменная Z назыв областью значений. Множество х-для ф-ции 2-ух переменных представляет собой некоторую плоскую фигуру или плоскость. Для ф-ции 3–х переменных область определения представляет собой 3-х мерное пространство или его часть. График ф-ции 2-ух переменных Z=f(х,у) представляет собой множество точек х,у,z. 3-х мерного пространства т.е. график представляет собой некоторую поверхность. Линия уровня ф-ции 2-ух переменных f(х,у)=С назыв множество точек плоскость таких что во всех этих точках значения ф-ции одно и то же и=с число с в этом случае назыв уровнем. Z=х во второй степени + у во второй степени. Линия уровня представляют собой концентрические окружности.
Предел
ф-ции нескольких переменных. Число
А назыв пределом ф-ции Z=f
(х,у) при х → х0 , у → у0, если для любого
положительного Е найдется положительное
б, зависящая от Е такое, что для всех
точек х и у, отстоящих от точек х0 и у0
на расстоянии меньшее, чем б выполнится
неравенство: │f(x,y)-A│˂E
А=предел х → х0 , у → у0 f(х,у).
ф-ция Z=f(х,у)
назыв непрерывной в точке х0 и у0, если
она:1. Определена в точке х0 и у0. 2.
Имеет конечный предел при х → х0 , у →
у0. 3. Этот предел = значению ф-ции в этой
точке. Пусть задана ф-ция Z=f(х,у)
зададим аргументу приращение ∆х и
соответственно у; ∆у. тогда ф-ция Z
также получит некоторое наращенное
значение. Введем величину
∆Z=f(x+∆x;y+∆x)-f(x;y).
∆Z
назыв полным приращение ф-ции в точке
х,у. Если задавать приращение ф-ции
только одного аргумента ∆х, тогда
величину ∆хZ=f(x+∆x,y)-f(x,y).
(∆yZ=f(x,y+∆y)-f(x,y)),которая
назыв частным приращением. Частной
производной ф-ции нескольких переменных
по одной из этих переменных назыв предел
отношения соответств частного приращения
ф-ции к приращению рассматриваемой
независимой переменной при стремлении
последнего к 0.
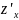 =
=
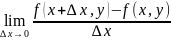
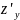 =
=
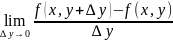 ;
=
;
=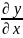 ;
=
;
=
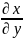 Замечание.
Для
нахождения частных производных по
одной из переменной, все другие переменные
явл величинами постоянными →можно
использовать табл производных и правила
дифф-ия для ф-ции с 1-ой переменной.z=3
Замечание.
Для
нахождения частных производных по
одной из переменной, все другие переменные
явл величинами постоянными →можно
использовать табл производных и правила
дифф-ия для ф-ции с 1-ой переменной.z=3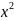 +6
+6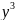 ,
,
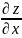 =6x,
=6x,
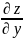 =18
=18 .
.
19. Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆хz. Итак,
Δхz=ƒ(х+Δх;у)-ƒ(х;у).
Аналогично получаем частное приращение z по у:
Δуz=ƒ(x;у+Δу)-ƒ(х;у).
Полное приращение Δz функции z определяется равенством
Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у).
Если существует предел
![]()
то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:
![]() Частные
производные по х в точке М0(х0;у0) обычно
обозначают символами
Частные
производные по х в точке М0(х0;у0) обычно
обозначают символами
![]() .Аналогично
определяется и обозначается частная
производная от z=ƒ(х;у) по переменной у:
.Аналогично
определяется и обозначается частная
производная от z=ƒ(х;у) по переменной у:
![]()
таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной). Геометрический смысл частных производных функции двух переменных : Графиком функции z= ƒ (х; у) является некоторая поверхность (см. п. 12.1). График функции z = ƒ (х; у0) есть линия пересечения этой поверхности с плоскостью у = уо. Исходя из геометрического смысла производной для функции одной переменной (см. п. 20.2), заключаем, что ƒ'x(хо;уо) = tg а, где а — угол между осью Ох и касательной, проведенной к кривой z = ƒ (х; у0) в точке Мо(хо;уо; ƒ(хо;уо)) (см. рис. 208).
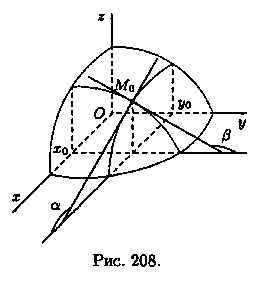
Аналогично, f'y (х0;у0)=tgβ.
20.Диференциал функция неск переменных. пусть задана функция 2-ух переменных z=f(x,y). Дифференциалом функции z наз. Сумма частных производных этой фун-ии на приращение независимых переменных, т.е. dz=z’x∆x+z’y∆y, dz=(∂z/∂x)*∆x+(∂z/∂y)∆y (1). Приращение ∆х- это есть dx, a ∆y=dy, тогда dz=(∂z/∂x)*dx+(∂z/∂y)*dy (2). Функция z=f(x,y) наз. Дифференцируемой в точке с координатами х,у, если ее полное приращение может быть представлено в виде ∆z=dz+α∆x+β∆y (3), где α=α(∆х,∆у), β=β(∆х,∆у) есть бесконечно малые фун-ии при ∆х, ∆у→0. Дифф-ал фун-ии 2-ух переменных, как и в случае одной переменной представляет главную часть линейную относительно ∆х и ∆у полного приращения фун-и. геометрический дифф-ал фун-ии dz есть приращение аппликаты касательной к плоскости k поверхности z=f(x,y). В данной точке, когда переменные х и у получат приращения ∆х и ∆у соответственно. Условия дифференцируемости фун-ии: для фун-ии нескольких переменных существование частных производных явл. необходимым условием дифференцируемости, но не явл. достаточным. Если частные производные фун-ии z=f(x,y) существуют в окрестности точки с координатами х,у, то фун-я z-дифференциируема в этой точке. Замечание: под окрестностью точки плоскости будем понимать круг (шар) с центром в этой точке.
21.Производная по направлению. производной для фун-ии z=f(x,y) по направлению L наз. предел отношения приращения фун-ии в этом направлении к величине перемещения ∆L при стремлении последней к 0. Z’L=lim∆L→0 ∆ZL/∆L. эта величина характеризует скорость направления L. Чаще всего производная по направлению выражается через частные производные Z’L=Z’x* cosα+Z’y*cosβ, где α и β-это углы, кот. образуют направление L с координатами осями. Градиент фун-ии: градиентом фун-ии z=f(x,y) наз. вектор, координатами которого явл. частные производные: перевернутый ∆z=(z’x; z’y ) (перевернутый треугольник – набла). Производная по направлению градиента есть скалярное произведение градиента фун-ии z и единичного вектора L с координатами cosα, cosβ, которая задает направление L. Градиент фун-ии задает направление наибольшего роста, а его длина скорость изменения фун-ии в этом направлении. Градиент фун-ии z в т. М (х,у) отличный от 0 перпендикуляно линии уровня, проходящий через эту точку.
