46. Поверхностный интеграл второго рода.
Пусть
S гладкая ориентированная пов-ть
.
Рассмотрим
которая
непр на пов-ти S.
Опр.
Поверхностным интегралом второго рода
по ориентированной пов-ти S называется
;
-векторная
запись пов интеграла второго
рода.
-координатная
запись;
вычисление поверхностного интеграла
второго рода сводится к вычислению
пов-ного интеграла 1-го рода. При изменение
пов-ти ,
меняет знак
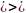при изменении ориентации пов-ти инт
2-го рода меняет знак те.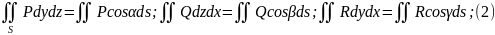
тк
где ds эл-т площадь, dxdy =эл-т площади пов-ти
S на плоскости (x,y); получим формулы для
вычисления по винт 2-го рода в декартовых
координатах.
Пусть
гладкая ориент пов-ть S задается любым
из след 3-ех способов: z=f(x,y) ,
;
Пусть пов-ть описывается формулой (3)
z-f(x,y)=0. Вектор нормали с точностью до
знака равен градиенту этой функции.
тк
,
то вектор од. Нормали
;
Если нормаль образует острый угол с
направлением оси z, которая задается
вектором
то
Вычислим
эти формулы справедливы и для остальных
равенст (2)
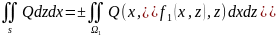
47. Скалярное поле, производная по направлению, градиент.
Пусть
Ω – область в
.
Опр1:
Скалярным полем U
на области Ω называется числовая ф-я
U(M),
опред в точках M
є Ω. В разных системах координат получим
одинаковые U(M).
Пов-ти, у которых U(M)=const
– пов-ти уровня. Они дают геометр хар-ки
ф-ии поля. Зададим в т.
направление с помощью вектора
;
;
- длина отрезка
;
Опр2:
Производной скалярного поля называется
предел
(1) Опр2 инвариантно т.к. в нём не использ
конкретн система координат.
Th.
Пусть скалярн поле U(M)
дифф-емо в т.
,
тогда для любого направлен, задан
вектором
,
существует производная по направлен,
которая вычисл по ф-ле
(2)
Производ
по направл обобщают частн производн.
Если
;
то это обычная част производн. Если
,
то поле возрастает, <0 – убывает.
Опр3:
Градиентом в т.
называется вектор gradU(M),
который в декарт системе координат
имеет вид
;
Можно дать инвариантное определение
градиента: он полностью определяется
полем и не зависит от системы координат.
(3) Пусть векторное поле дифф-емо в т.
,
тогда, если градиент
,
то он определяется как вектор, удовл
2услов: 1) его длина равна максимальной
величине производной в этой точке, 2)
любое направление вектора совпадает с
направлением
,
по которому производная максимальна.
Т.к.
,
то из (3) вытекает:
48. Векторное поле, векторные линии, поток векторного поля.
Пусть Ω – область на
Опр1:
Векторным полем на области Ω назыв
вектор-ф-я
,
заданная в точках М є Ω.
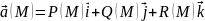
Опр2: Векторной линией векторн поля назыв гладкая кривая, которая в каждой своей точке касается векторн поля .
Выведем
дифф уравн для нахожд этих линий:
касательная задаётся вектором
.
Если кривая касается поля
,
то вектор касательной и вектор
пропорциональны.
.
Поток
вектор поля: Пусть
.
Пусть на этом замыкании задано непрерыв
векторн поля, т.е. ф-ии P,Q,R
– непрер. Зададим гладк пов-ть в обл Ω,
т.е. в кажд точке этой пов-ти сущ касат
пл-ть, непрер зависящая от точки. Также
у неё есть единич нормаль
,
которая также непрер зависит от точки.
Опр3:
Пов-ть S,
у которой фиксирована одна из ориентаций,
назыв ориентированной.
Опр4: Потоком вект поля через ориентриован пов-ть S, ориентация которой задаётся с помощью единич вектора нормали , называется поверхностным интегралом I рода по пов-ть S по проекции векторн поля на единич нормаль
.
Он сходится. ||| Поток для жидкости. рассм
стандартн течен жидкости, тогда вектор
скорости жидкости зависит от точки и
не зависит от времени. Поток равен кол-ву
жидкости, которое проходит через пов-ть
S
в напр, куда ориентирована пов-ть.
49. Формула Остроградского-Гаусса.
50. Дивергенция векторного поля
О-Г
51. Циркуляция и ротор векторного поля. Инвариантное определение ротора.
52. Формула Стокса.
Пусть G – некот. огр. обл-ть в и в этой обл-ти рассмотрим кус. глад. пов-ть S с кус. глад. гр. Г которая ориентир. согласовано с пов-тью S.
Th.
Пусть ф-ии P,Q,R а также их частные
производные непр. в обл-ти G тогда для
вект. поля
=(P,Q,R)
справ-ва ф-ла
–
ф-ла Стокса. Она выражает тот факт, что
поток ротора
через пов-ть S, огранич. контуром Г, равен
циркуляции вект. поля
по контуру Г.