1. Определение определённого интеграла. Необходимое условие интегрируемости.

2. Суммы Дарбу. Интегрируемость непрерывных функций.

3. Свойства определенных интегралов.

4. Оценки интегралов. Теорема о среднем значении.

5.Определенный интеграл с переменным верхним пределом. Непрерывность интеграла по верхнему пределу.

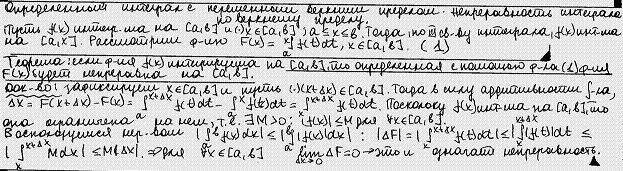
6.Дифференцируемость интеграла по верхнему пределу. Формула Ньютона-Лейбница.

7. Замена переменных и интегрирование по частям в определенном интеграле.

8. Вычисление площадей в декартовых и в полярных координатах.

9. Вычисление длины параметрически заданной кривой. Длина кривой в декартовых и полярных координатах.

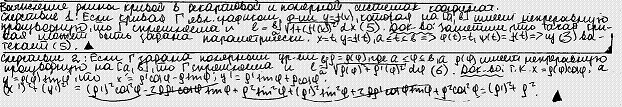
10. Вычисление объёма тела вращения

11. Определения несобственных интегралов. Критерий сходимости.

12. Признаки сравнения для несобственных интегралов

13. Абсолютная и условная сходимость интегралов. Признак Дирихле.

14. Понятие функции многих Переменных. Предел функции многих переменных.

15. Множества в n - мерном пространстве.

16. Непрерывность функции многих переменных. Свойства непрерывных функций

17. Непрерывность сложной ф-и.

18. Частные производные. Дифф-ть ф-и многих перем. Связь дифф-ти и непр-ти.

19. Необходимое и достаточное условия диффернц-ти.

20. Дифференциал и его связь с приращением функции.

21.Касательная плоскость и нормаль к поверхности, заданной уравнением

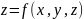
22. Производная сложной функции.

23. Частные призводные высших порядков. Теорема о равенстве смешанных производных.

24. Дифференциалы высших порядков

25. Инвариантность формы первого дифференциала. Неинвариантность формы дифференциалов порядка выше первого.

26. Формула Тейлора для функции многих переменных.

27. Локальный экстремум функции многих переменных. Необходимое условие экстремума.

28. Достаточные условия существования локального минимума (максимума) функции многих переменных. Условие отсутствия экстремума.

29. Понятие об условном экстремуме.

30. Непрерывность интеграла, зависящего от параметра.

Рассмотрим прямоугольник: D={(x,y) }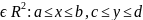

a<b, c<d – некоторые константы. Пусть функция f(x,y) опр. В прямоугольнике D, тогда сможем рассмотреть: F(x) = (1) Данный интеграл берется по переменной у. Интеграл (1) зависит от х. Говорят, что инт(1) зависит от параметра х.

Th. Если функция f(x,y) непр. в D, то тогда F(x) непр. на [a,b].

Следствие интеграл от F(х) по [a,b] – повторный интеграл. Если F(x) непрерывна, то она интегрируема.

31.Объем криволинейного цилиндра. Двойной интеграл.

32 .Свойство Двойного интеграла. Теорема о среднем значении.

Св-ва двойного инт. Аналогичны св-вам одномерного инт.

1. Св-во линейности

Функция 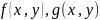интегр. На облости 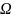, а A и B произвольные константы. Тогда ф-ия 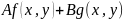так же интегрируема на обл-ти , причем вып-ся равенство:

2. Св-во аддитивности

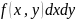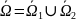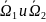Пусть ф-ия интегр. На обл-ти , такой, что , где - огранич области с кусочно-гл границами и 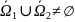, тогда ф-ия 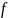интегр. На каждой из областей 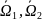причем

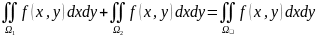
3. Св-во

Если , 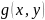инт. На обл-ти , и на этой обл-ти вып-ся нер-во : 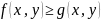то тогда

4. Св-во

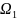Если инт. На обл-ти , то тогда так же инт на области и справедливо нер-во:

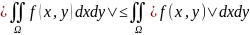
Th. О среднем значении

Пусть ф-ия 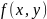непрерывна на 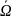, где – ограниченная область такая , что мн-во связано, тогда существует точка 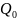такая , что и выполняется рав-во

33. Сведение двойного интеграла к повторным.

Th. Пусть ф-я непрер-на на замкнутости D, 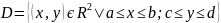, тогда справ-во рав-во (2). Замеч-е: в левой части ф-лы (2) стои двон интег от ф-ии f по замкн D и т.к. f непрер на D, то D явл огран мн-вом с замыканием огран обл-ти с кус-гл гран-й, то двойн интегр существует. Кроме того, существ повторн интегр-ы в ф-ле (2). Теорема утверждает рав-во между двойн и повторн интегр-ми, давая способ вычсл-я двойн интегр.

34. Замена переменных в двойном интеграле. Случай линейного отображения.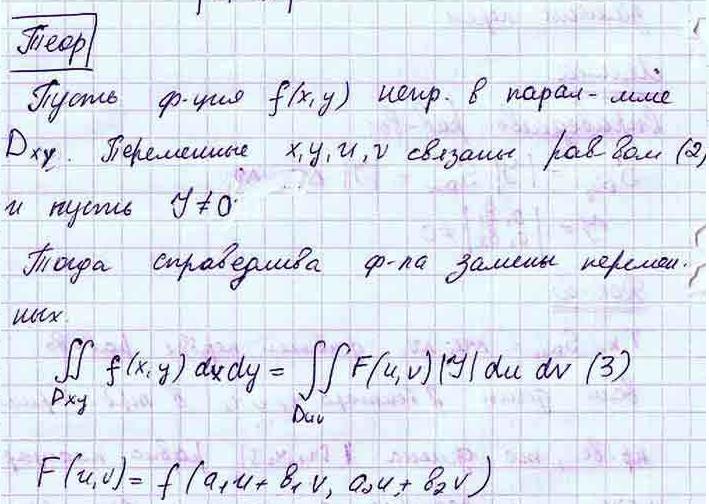

35. Замена переменных в двойном интеграле. Двойной интеграл в полярной системе координат.

36. Тройной интеграл.

37. Свойства тройных интегралов. Теорема о среднем.

38. Сведение тройного интеграла к повторным интегралам.

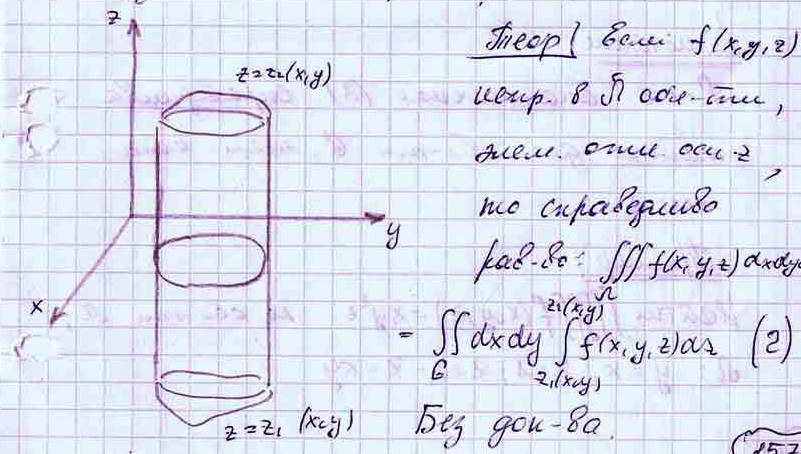
39. Замена переменных в тройном интеграле. Сферические и цилиндрические координаты.

Цилиндрическая система координат.

Связь координат произвольной точки Р пространства в цилиндрической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

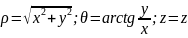
Для представления тройного интеграла в цилиндрических координатах вычисляем Якобиан:

Итого:

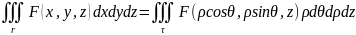
Сферическая система координат.

Связь координат произвольной точки Р пространства в сферической системе с координатами в декартовой прямоугольной системе осуществляется по формулам:

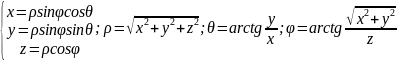
Для представления тройного интеграла в сферических координатах вычисляем Якобиан:

Окончательно получаем:

40. Определение и свойства криволинейного интеграла 1-го рода.

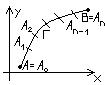
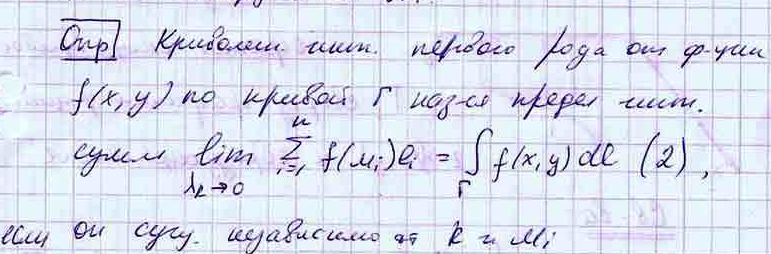масса кривой Г

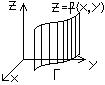
Свойства:

1.f(x,y)=1, .

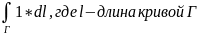2. Криволинейный интеграл 1 рода не зависит, в каком направлении: от А к В, либо от В к А продвигает.

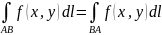
3. Линейность. Если у f(x,y), g(x,y) существует кратный интеграл 1 рода по Г, где α,β – производные const, то для функции αf(x,y)+βg(x,y) также сущ-ет криволинейный интеграл 1 рода по кривой Г.

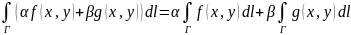
4. Аддитивность. Пусть кривая AB состоит из 2 дуг: АС и СВ, и существует криволин. Интеграл 1 рода от функции f(x,y) по AB, тогда сущ-ют криволинейные интегралы от функции F по каждой из дуг АС и СВ, вып-ся равенство

Замечание: мы дали определение криволин. интеграла для плоской кривой Г. Совершенно аналогично определяется криволинейный интеграл 1 рода для гладкой простр. Кривой Г, которая задаётся параметрически в виде x= (t), y=ψ(t),z= (t), a≤t≤b(3). Здесь функции φ,ψ,χ непрерывны вместе с первыми производными на отр. [a,b] и выполняется условие (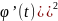 + ) 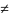0.

41.Вычисление криволинейного интеграла 1-го рода.

Для декартовых и полярных вместо длины кривой параметрически заданной, подставляем нужную длину.

42. Криволинейные интегралы 2-го рода.

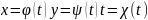
Кривая Г задана параметр-ки (1)

Опр Криволинейным интегралом 2го рода от 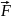(x,y,z) на простр. кривой Г наз-ся предел инт. сумм

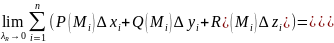
Если d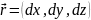 то можно инт (2) в виде

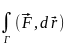
Физ смысл - работа по перемещению мат. точки вдоль кривой Г из А в B под действием силы

1св-во линейность

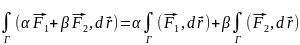
2св-во аддитивность

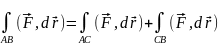
3св-во (в отличие от 1го рода)

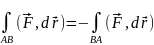
43. Формула Грина.

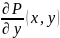
Th Пусть ф-ции P(x,y) Q(x,y) и част производные 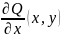непрерывны на замыкании ограниченной области Ω с кус.гл. границей Г, справедливо равенство

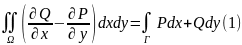
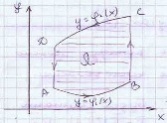
Интеграл в правой части представаляет собой сумму интегралов по связным компонентам положительно ориентированной границы Г области Ω

44. Площадь поверхности. Вычисление площади поверхности.

45. Поверхностный интеграл первого рода.

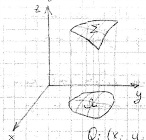  Пусть пов-ть Σ задана ур-ем z=f(x,y), (x,y) ) Ω(3), где Ω огранич облость с кус-гл границей, и ф-ция f вместе с 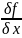, 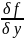непр на Ω. И пусть на поверхности Σ задана некоторая ф-ция от 3 переменных U(x,y,z).

Разобьём Ω на N частей:

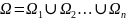
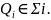
Данные области могут пересекаться или по своим кусочно-гл границам. Разбиение R обл-ти на N частей приводит к разбиению пов-ти Σ на N частей. На каждом из кусков Σi выбираем произвольную точку 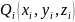где z=f( ; )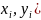

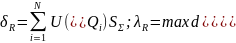Опр. Поверхностным интегралом 1-го рода от ф-ции u(x,y,z) по пов-ти Σ называется предел инт сумм 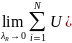если она сущ и независет от выбора R и выбора точек Q.

Замечание. Ф-лы аналогичные формуле(5) справедливы также для пов-тей, заданных ур-ми y=f1(x.z) или x=f2(y,z) ; в случае более сложных поверхностей и следует разбить на куски, которые однозначно проектируются на одну корд плоскостей, вычислить по найденным фрагментам значение интегралов а затем из сложить.