3. Знакочередующиеся ряды. Абсолютная и условная сходимость.

Знакопеременные ряды. Абсолютная и условная сходимость.

Особенно часто среди знакопеременных рядов встречаются ряды, члены которых имеют чередующиеся знаки, т.е. знакоче­редующиеся ряды.

Условимся считать первый член ряда положительным; тогда знакочередующийся ряд в общем виде запишется так:

(1)

где все а_п положительны (n = 1,2, ...).

u₁ + u₂ + u₃ + . . . + u_n + . . .(1)-знакопеременный ряд

|u₁| + |u₂| + |u₃| + . . . + |u_n| + . . . (2) –знакопеременный ряд, составленный из абсолютных величин его членов.

(*)

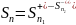Ряд 1 называют абсолютно сходящимся, если сходится ряд 2, составленный из модулей его членов. Справедливо и обратное утверждение.

Ряд 1 называют условно сходящимся, если ряд 1 сходится, а ряд 2 расходится.

3. Признак Лейбница.

Признак лейбница для знакочередующихся числовых рядов.

(теорема Лейбница). Если члены знакочереду­ющегося ряда убывают по абсолютной величине и стремят­ся к нулю, когда п →∞, то 1) ряд сходится; 2) любой остаток ряда не превосходит по абсолютной величине первого из сво­их членов и имеет одинаковый с ним знак.

3. Степенные ряды.

Степенные ряды.

Ряд вида a₀+a₁x+a₂x²+…+a_nxⁿ+… (1)

Где a_0, а₁, а₂,…,а_n,…-некоторая числовая последовательность, называют степенным рядом.

a_0, а₁, а₂,…,а_n- коэффициенты степенного ряда

3. Радиус сходимости.

Круг сходимости степенного ряда

— круг вида

, ,

в котором ряд абсолютно сходится, а вне его, при , расходится. Иными словами, круг сходимости степенного ряда есть внутренность множества точек сходимости ряда. Радиус круга сходимости называется радиусом сходимости ряда. Круг сходимости может вырождаться в пустое множество, когда , и может совпадать со всей плоскостью переменного , когда .

Радиус сходимости

Радиус круга сходимости называется радиусом сходимости ряда.

Радиус сходимости ряда Тейлора аналитической функции равен расстоянию от центра ряда до множества особых точек функции, и может быть вычислен по формуле Коши — Адамара:

Эта формула выводится на основе признака Коши.

3. Интервал сходимости. Область сходимости.

Множество U с R называется областью сходимости функционального ряда , если для каждого значения x0ϵU сходится числовой ряд ,, а для x не принадлежащем U числовой ряд расходится.

, где R-радиус сходимости

(x0-R, x0+R)-интервал сходимости. На всем этом интервале ряд сходится.

3. Ряды Тейлора и Маклорена.

Ряды Тейлора (Маклорена)

Если ф-я бесконечно диф-ма на некотором интервале (x0 − R, x0 + R) и имеет ограниченные производные |f⁽ⁿ⁾(x)| < MϵR, для всех x ϵ (x0 − R, x0 + R) и n ϵ N, то на этом интервале справедливо равенство:

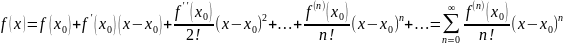
Если х₀=0, то ряд Тейлора можно записать в виде:

Он называется рядом Маклорена.

3. Разложение в степенной ряд элементарных функций.

Приступим к увлекательному занятию – разложению различных функций в степенные ряды. Сначала пара формул, затем практические задания.

Если функция  в некотором интервале раскладывается в степенной ряд по степеням , то это разложение единственно и задается формулой: Примечания: Надстрочный индекс  в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву .

Данная формула получила имя некоего англичанина Тейлора (ударение на первый слог).

На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда :

Это разложение в ряд обычно называют именем шотландца Маклорена (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора  по степеням .

Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции: Как оно получилось? По формуле Маклорена: Рассмотрим функцию , тогда:

Теперь начинаем находить производные в точке ноль: первую производную, вторую производную, третью производную и т.д.  Это просто, поскольку при дифференцировании экспонента превращается в саму себя:

И так далее….

Совершенно очевидно, что

Подставляем единицы в формулу Маклорена и получаем наше табличное разложение!

Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).