3. Дифференциальные уравнения второго порядка с постоянными коэффициентами.

Уравнение  вида y''+ρy'+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным  дифференциальным  уравнением   с   постоянными   коэффициентами. Рассмотрим линейное  уравнение   второго   порядка  вида:       y''+ρy'+qy=0, (1) у которого правая часть f(x) равна нулю. Такое  уравнение  называется однородным. Уравнение  K²+ρK+q=0 (2) называется характеристическим  уравнением  данного  уравнения  (1). Характеристическое  уравнение  (2) является квадратным  уравнением , имеющим два корня. Обозначим их через К₁ и К₂. Общее решение  уравнения  (1) может быть записано в зависимости от величины дискриминанта D=ρ²–4q  уравнения  (2) следующим образом: 1. При D>0 корни характеристического  уравнения  вещественные и различные (К₁≠К₂), и общее решение имеет вид  . 2. При D=0 корни характеристического  уравнения  вещественные и равные (К₁=К₂=К), и общее решение имеет вид:  3.Если D<0, то корни характеристического  уравнения  комплексные:  , где   – мнимая единица,   и общее решение (К₁=α+βi, К₂=α–βi, β≠0), имеет вид y=e^αx(C₁ cosβx+C₂ sinβx).

3. Дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью.

4. Числовые ряды: их сходимость и расходимость.

Сумма конечного числа первых членов ряда:

называют частными суммами ряда (1). Т.к. число членов ряда бесконечно, то частичные суммы образуют последовательность (2)

Ряд (1) называют сходящимся, если последовательность (2) его частичных сумм сходится к некоторому числу S . в этом случае число S называют суммой ряда (1). В противном случае ряд- расходящийся.

В случае сходимости записывается

3. Необходимые условия сходимости.

Если ряд сходится, то предел его общего члена равен 0.

(если предел общего члена не равен нулю или не существует, то данный ряд расходится)

Доказательство:

Пусть данный ряд сходится и его сумма равна S. Для любого натурального n имеем или (3)

При n→∞ обе частичные суммы стремятся к пределу S, поэтому из равенства (3) следует, что .

3. Свойства сходящих рядов.

Свойства сходящихся рядов

1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.

2. Если ряд сходится, то .

3. Если ряд сходится, то сходится ряд и имеет место равенство =c

4. Если ряды и сходятся, то сходится и ряд имеет место равенство = +

3. Эталонные ряды.

4. Ряды с положительными членами.

Определение. Ряд

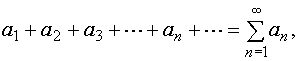
все члены которого неотрицательны, называется знакоположительным.

Теорема 5 (критерий сходимости знакоположительных рядов). Для того, чтобы знакоположительный ряд сходился, необходимо и достаточно, чтобы его частичные суммы были ограничены сверху (в совокупности), т. е. .

Доказательство

1. Необходимость. Пусть положительный ряд (1) сходится. Это значит, что существует предел 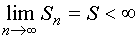. Кроме того, последовательность частичных сумм {S_n} –  возрастающая, т. к. ряд знакоположительный. Тогда S_n <S, т. е. последовательность {S_n} ограничена и роль числа М выполняет число S.

2. Достаточность. По условию члены последовательности частичных сумм 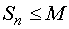, т. е. последовательность {S_n} ограничена сверху. К тому же она монотонно возрастает, т. к. ряд — знакоположительный. Поэтому по теореме “ всякая монотонно возрастающая, ограниченная сверху последовательность имеет предел” существует , то есть ряд (1) сходится.

Все признаки сходимости и расходимости положительных рядов в конечном счёте основаны на этой простой теореме, но непосредственное её применение лишь в редких случаях позволяет судить о характере ряда.

3. Признак Даламбера. Интегральный признак Коши.

Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами.

Первый признак сравнения.

Пусть даны два ряда с положительными членами:

Причем члены первого ряда не превосходят соответствующие члены второго ряда: . Тогда из сходимости ряда (2) («большего») следует сходимость ряда (1) («меньшего»). Эквивалентно- из расходимости меньшего следует расходимость большего.

Второй признак сравнения

Если для рядов (1) и (2) с положительными членами существует отличный от нуля предел отношения

, (4)

то ряды (1) и (2) сходятся или расходятся одновременно.

Признак Даламбера

Если для ряда с поло­жительными членами a₁ + а₂+... + а_n +... существует такое чис­ло q < 1, что при всех n (или начиная с некоторого n) выпол­няется неравенство

(6)

то ряд сходится. Если же > 1 для всех или начиная с некоторого n, то ряд расходится