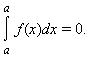1. Неопределенный интеграл, его свойства. 2. Таблица основных интегралов. 3. Интегрирование заменой переменной. 4. Интегрирование по частям. 5. Интегрирование рациональных дробей. 6. Интегрирование тригонометрических функций. 7. Интегрирование некоторых видов иррациональностей. 8. Определенный интеграл, его свойства. 9. Вычисление определенных интегралов способом подстановки и по частям. 10. Приближенное вычисление определенных интегралов. 11. Геометрические приложения определенного интеграла: вычисление площадей фигур, объемов тел. 12. Несобственные интегралы с бесконечными пределами интегрирования 13. Несобственные интегралы от неограниченных функций. 14. Несобственные интегралы от разрывных функций. 15. Понятие о дифференциальном уравнении. 16. Дифференциальное уравнение первого порядка. 17. Общее и частное решение дифференциальных уравнений. 18. Дифференциальные уравнения с разделяющимися переменными. 19. Однородные дифференциальные уравнения первого порядка. 20. Линейные однородные дифференциальные уравнения первого порядка. 21. Уравнения Бернулли. 22. Однородные дифференциальные уравнения второго порядка. 23. Характеристическое уравнение. 24. Дифференциальные уравнения второго порядка с постоянными коэффициентами. 25. Дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью. 26. Числовые ряды: их сходимость и расходимость. 27. Необходимые условия сходимости. 28. Свойства сходящих рядов. 29. Эталонные ряды. 30. Ряды с положительными членами. 31. Признак Даламбера. 32. Интегральный признак Коши. 33. Знакочередующиеся ряды. 34. Признак Лейбница. 35. Абсолютная и условная сходимость. 36. Степенные ряды. 37. Радиус сходимости. 38. Интервал сходимости. Область сходимости. 39. Ряды Тейлора и Маклорена. 40. Разложение в степенной ряд элементарных функций. 41. Приложение степенных рядов к приближенным вычислениям.

1. Неопределенный интеграл, его свойства.

Функция F(x) называется первообразной для функции f(x) на промежутке Х если в каждой точке х этого промежутка выполняется равенство F’(x)=f(x)

Геометр.смысл. по геометрич. Смыслу производной F’(x) есть угловой коэффициент касательной проведенной к графику F(x) в точке х следоват. Геометр. Найти первообразную для функции f(x) значит найти такую кривую y=F(x) угловой коэффициент касательной который численно равен значению функции f(x) в точке х.

Графики первообразных получают движением функции F(x) вдоль оси ОУ.

Теорема. Пусть функции F₁(x), F₂(x) есть первообразные для функции f, тогда F₂(x)= F₁(x)+с

Док –во. F’₁(x)=f(x) ; F’₂(x)=f(x)

Рассмотрим (F₁(x)-F₂(x))’= F’₁(x)- F’₂(x)= f(x)- f(x)=0, тогда по теореме Лагранжа существует такое С, что (F₁(x)-F₂(x))’=c’

F₁(x)-F₂(x)=c

F₂(x)= F₁(x)+c

Действие нахождения первообразной для функции f(x) называется интегрированием каждая непрерывная имеет первообразную, а семейство или множество неопределенным интегралом f(x)dx=F(x)+c

Свойства неопределенного интеграла.

1.производная от неопределенного интеграла равна под интегральной функции

(f(x)dx)’=(F’(x)+c=f(x)(f(x)dx)’=f(x)

2.интеграл от производной равен под интегральной функции

F’(x)dx=f(x)dx=F(x)+c

3.постоянный множитель можно выносить за знак неопределенного интеграла

2. Таблица основных интегралов

(f(x)+-g(x))dx=f(x)dx+-g(x)dx

0dx=c

kdx=kx+c

xⁿdx= x^n-1/n+1+c, n≠-1

dx/x=lnx+c

a^xdx=а^x/lna

e^xdx=e^x+c

1/cos²xdx=tgx+c; dx/sin²x=-ctgx+c;xdx/ax²+b=1/2a*lnax²+b+c;

dx/x²-a²= 1/2a*lnx-a/x+a+c

3. Интегрирование заменой переменной.

Рассмотрим неопределенный интеграл F(x) некоторой функции f(x). Для упрощения вычисления интеграла часто удобно выполнить замену переменной. Переход от x к новой переменной u описывается выражением

где x = g (u) - подстановка. Соответственно, обратная функция u = g ⁻¹(x) описывает зависимость новой переменной от старой.

Важно иметь ввиду, что дифференциал dx должен быть заменен на дифференциал новой переменной du.

Для определенного интеграла, кроме этого, необходимо также изменить пределы интегрирования.

Пример 1

Вычислить .

Решение.

Сделаем замену . Тогда . Следовательно, интеграл принимает вид

     

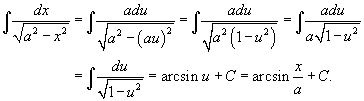
3. Интегрирование по частям.

(uv)’=u’v+uv’

F’(x)=f(x)

f(x)ax=F(x)+c

(u’v+uv’)dx=uv

du/dx*vdx+u*dv/dx*dx=uv

vdu+udv=uv

udv=uv-vdu

При решении интегрирования по частям под интегральное выражение делим на 2 множителя и который затем дифференцируем 2ой множитель за dv и который затем интегрируем поэтому во 2ой множитель относим dx и выбираем множитель интеграл от которого существует

3. Интегрирование рациональных дробей.

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.

1)если дробь не правильная

Pn(x)/Qm(x)*dx, nm – необходимо выделить целую часть, а потом проинтегрировать каждое слагаемое

2)если дробь правильная

Pn(x)/Qm(x)*dx, nm

А) dx/ax²+bx+c=необходимо выделить полный квадрат и выделенное выражение заменить новой переменной

b) dx/(x-x₁)(x-x₂)…(x-x_n)= если в знаменателе стоит многочлен то необходимо разложить этот многочлен простейшие множители, затем разложить под интегральную дробь на сумму простейших дробей, знаменатель под знаком интеграла дробь на сумму и найти интеграл от каждой дроби=1/(x-x₁)(x-x₂)…(x-x_n)=A/ x-x₁+B/ x-x₂+…+C/ x-x_n методом неопределенного коэффициента находим а, б, с.

3. Интегрирование тригонометрических функций.







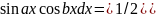
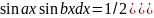
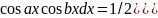
1)

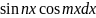
Если хотя бы одна степень n или m не четная то выделяем у этой не четной степени множитель 1ой степени и вводим новую переменную

2) если m и n четные то используем формулы понижения степени

Sin² x/2= 1- cos x/2

Cos² x/2= 1+cosx/2

Если подынтегральная функция dx четная то делаем подстановку tg x=t

3. Интегрирование некоторых видов иррациональностей.

(Интегрируем по частям при условии dx=dv, а остальное v arcsin, arcos, arctg, arcctg)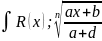 *dx=ad-cb≠0; 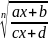=t

ax+b=tⁿ(cx+d)

ax-ctⁿx=td-b

x*(a-ctⁿ)=tⁿd-b

x= dxⁿ-b/a-ctⁿ

3. Определенный интеграл, его свойства.

Рассмотрим фигуру ограниченную сверху не прерывной не отрицательной функции f(x) слева и справа прямымиx x=a? X=b, снизу осью OX и называют ее криволинейной трапецией.

Разобьем отрезок от а до b на n равных частей

Пусть [a;x₁]= x₁ и т.д. с₁ϵ[a;x₁], f(a)

Построим прямоугольник на отрезке х₁ и высотой fc₁

Аналогично возьмем точки с₂,с₃ и с_n и т.д. найдем fc₂, fc₃, и fc_n и построим прямоугольник

S₁= x₁*f(c₁) и т.д.

S ст.ф.=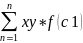

S ст.ф.Sкр.тр.n

Если при n (x_n0) существует конечный предел интегральной суммы (суммы Римана) не зависящей от способа разбиения, а зависит от выбора точки с то f(x) называется интегрируемой функцией на промежутке от а до в , а сам промежуток определяется интегралом.

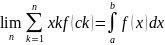
Свойства определенного интеграла

1. 

2)общий множитель можно выносить за знак определенного интеграла. Определенный интеграл алгебраическая сумма равна сумме определенного интеграла от каждого слагаемого с теми же пределами интегрирования.

3)активности – если непрерывная функция f(x) интегрируема на наибольших из отрезков то она будет интегрируема и на остальных.

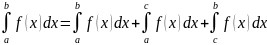
4)теорема о среднем если функция f непрерывна на отрезке от а до в то найдется хотя бы одна точка с такая, что определенный интеграл f(c)(b-a)=f(x)dx

5) если f(x)g(x)



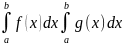
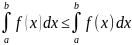
6)определенный интеграл не зависит от переменной а зависит от предела интегрирования.

3. Вычисление определенных интегралов способом подстановки и по частям.

Интегрирование подстановкой (заменой переменной)

Пусть для вычисления интеграла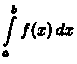 от непрерывной функции

сделана подстановка х = φ(t).

Теорема

Если:

1) функция х = φ(t) и ее производная х' = φ'(t) непрерывны при t є [а;β];

2) множеством значений функции х = φ(t) при t є [а,β] является отрезок [а; b];

3) φ(а)=а и φ(β)=b.

то

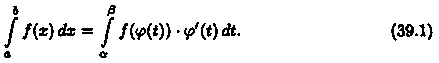
▼Пусть F(x) есть первообразная для ƒ(х) на отрезке [а;b]. Тогда по формуле Ньютона-Лейбница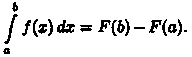 Так как (F(φ(t))' = f(φ(t)) - φ'(t), то F(φ(t)) является первообразной для функции f(φ(t)) -φ'(t), t  [а;β]. Поэтому по формуле Ньютона—Лейбница имеем

▲

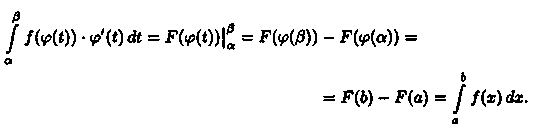Формула называется формулой замены переменной в определенном интеграле. Отметим, что:

1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется;

2) часто вместо подстановки х = φ(t) применяют подстановку t = g(x);

3) не следует забывать менять пределы интегрирования при замене переменных!

 

Интегрирование по частям

Теорема

Если функции u = u(х) и v = v(x) имеют непрерывные производные на отрезке [а; b], то имеет место формула

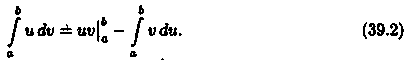
На отрезке [а; b] имеет место равенство (uv)' = u'v+uv'. Следовательно, функция uv есть первообразная для непрерывной функции u'v+uv'. Тогда по формуле Ньютона-Лейбница имеем:

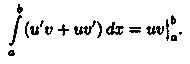
Следовательно,

▲

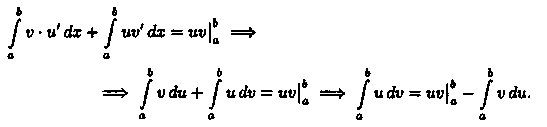Формула называется формулой интегрирования по частям для определенного интеграла.

3. Приближенное вычисление определенных интегралов.

4. Геометрические приложения определенного интеграла: вычисление площадей фигур, объемов тел.

1)S криволинейной трапеции

S=

2. S= =-

3. S= = + +

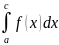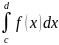4. S= 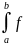₁(x)dx- ₂(x)dx=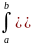 ₁(x)-f₂(x))dx

Рассмотрим криволинейную трапецию ограниченную сверху функцией f(x) которую начнем вращать относительно оси ОХ и ОУ.

V= ²(x)dx

S_{бок.пов.}=2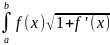 ²dx

3. Несобственные интегралы с бесконечными пределами интегрирования

Пусть (х) непрерывна на

Тогда функция Ф(b) = является непрерывной функцией от b при

О: Несобственным интегралом (нс. и.) от непрерыв-

ной на функции (х) называется

Если указанные пределы существуют и конечны, то интегралы называются сходящимися, в противном случае — расходящимися.

Обозначим

— обобщенная формула Ньютона—Лейбница.

Пример:

О: Несобственным интегралом от непрерывной на

функции (х) называется

Он сходится, если сходятся оба интеграла справа, и расходится, если расходится хотя бы один из них. Геометрический смысл

сходящегося несобственного интеграла при заключается в том, что его можно трактовать как площадь бесконечной криволинейной трапеции с границей (рис. 17.4).

Во многих случаях бывает достаточно установить, сходится ли данный интеграл. Такой вопрос решается применением признаков сходимости. Приведем без доказательства признак сравнения для неотрицательной функции.

Т: Пусть для всех выполняется неравенство

Тогда

а) если сходится то сходится и

б) если расходится то расходится и

Пример: Исследовать на сходимость

Так как при а сходится (см. предыдущий пример), то и данный интеграл — сходящийся

Для (х), принимающей при значения разных знаков, применяется следующий признак сходимости.

Теорема: Если сходится, то сходится и

Признаки переносятся и на