
- •Пример 1
- •Несобственные интегралы от неограниченных функций.
- •Если подынтегральной функции не существует в точке
- •Несобственные интегралы от разрывных функций.
- •Понятие о дифференциальном уравнении.
- •Дифференциальное уравнение первого порядка.
- •Дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •Доказательство
- •Знакочередующиеся ряды. Абсолютная и условная сходимость.
- •Признак лейбница для знакочередующихся числовых рядов.
- •Радиус сходимости
- •Приложение степенных рядов к приближенным вычислениям.
- •Разложение некоторых функций в ряд Маклорена
Дифференциальное уравнение первого порядка.
ДУ вида F(x;y;y’)=0 (1) называют ДУ 1ого порядка, а уравнение y’=f(x;y) (2) называют ДУ1ого порядка с разрешенным относительно производной.
Т.к. решение ДУ (2) задает семейство интегральных кривых то для построения необходима хотя бы одна точка принадлежащая этой кривой. Назовем эту точку начальным условием (x0,y0)
y(x0)=y0
y/=y0(3) начальное условие
х=х0
тогда можно найти семейство касательной через угловой коэффициент к и (х0,у0) которые будут образовывать поле направлений и если существует такая прямая которая ограничена или задает одинаковое направление поля то она называется изокменой.
ДУ (2) может быть записано в виде dy/dx=f(x;y)
dy=f(x;y)dx
P(x;y)dy+Q(x;y)dy=0 (4)
Уравнение (4) удобно тем, что переменные в этом уравнение (х,у) равноправны.
Самым простым видом ДУ (4)
P(x)dx+Q(y)dy=0 например xdx+ydy=0
Ydy=-xdx
ydy=-xdx
y2/2=-x2 получим y2+x2≠c
Общее и частное решение дифференциальных уравнений.
Если решение записано в неявной форме то его называют общим интегралом.
Для ДУ 1ого порядка различают частное и общее решение. Функция y=(x;c) называют общим решением если она удовлетворяет след. условиям:
1)она является решением ДУ при каждом фиксированном с.
2) каковы бы не были условия 4 можно найти такое решение с=с0
у=(х,с0) является решением ДУ удовлетворяющим начальным условиям
уравнение y=(x;c0) называется частным решением.
Решить ДУ значит решить задачу Коши.
Теорема. О существовании и единичности решения задачи Каши. Если f(x;y) и ее частная производная f’y(x;y) непрерывны в некоторой области Д содержащей точки x0,y0 то существует единственное решение у=(х) удовлетворяющее начальным условиям 4.
Дифференциальные уравнения с разделяющимися переменными.
P1(x)Q1(y)dx+P2(x)Q2(y)dy=0 - называют ДУ с разделяющимися переменными
 +
+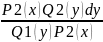 =
=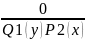
 dx+
dx+ dy=0
– ДУ с разделёнными переменными.
dy=0
– ДУ с разделёнными переменными.
Q1(y)P2(x)=0 – особое решение, если она существует.
(y+yx)dx+(x-xy)dy=0
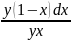 +
+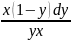 =0
=0
 dx+
dx+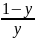 dy=0
dy=0
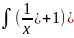 dx+
dx+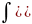 )dy=
)dy=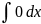
LnIxI+x+Lny-y=c
LnIxyI+x-y=c – получили общий интеграл
(xo; yo)=(1,2)
Ln2+1-2=c
c=Ln2-1
LnIx-yI+x-y=Ln2-1 – частное решение или частный интеграл
Однородные дифференциальные уравнения первого порядка.
Рассмотрим функцию f(x;y), если при умножении каждого аргумента на множитель «ланда» сама функция увеличивается в «ланда» степени k раз, то функция называется однородной, то есть f(ланда x, ланда y)= ланда в степени k f(x,y)
Пример:
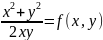
 - функция однородна.
- функция однородна.
Если f(x;y) в уравнении однородная, то и всё уравнение однородное.
Линейные однородные дифференциальные уравнения первого порядка.
y’+p(x)y=g(x) – линейное дифференциальное уравнение, где p(x) и g(x) – заданные функции в частности постоянные. Особенностью этого уравнения является, то что производная и функция не перемножаются.
Решение ищут с помощью подстановки
1 шаг. y=uv, u=u(x), v=v(x)
y’=u’v+uv’
u’v+uv’+p(x)uv=g(x)
u’v+u(v’+p(x)v)=g(x)
Подберем функцию v таким образом чтобы вся скобка =0
v’+p(x)v=0 – уравнение с разделяющимися переменными
 =
-p(x)v/dx
=
-p(x)v/dx
 /:v
/:v
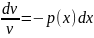
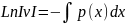

2 шаг.
u’v=g(x)
u’=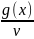
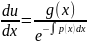
 /dx
/dx
 dx
dx
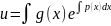 dx
dx
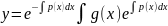 dx
dx
Уравнения Бернулли.
y’+p(x)y=g(x)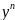 – уравнение Бернулли.
– уравнение Бернулли.
Разделим всё на
y’ +p(x)
+p(x)
 =z
=z
z’=(-n+1) y’
y’

Решается методом подстановки z=uv или методом Лагранжа
Пример:
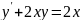



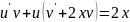

 /
/
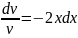
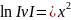

u’v=2x
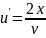
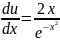 /*dx
/*dx




Метод Лагранжа – это метод вариации произвольной переменной
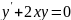
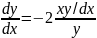

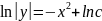






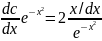


Однородные дифференциальные уравнения второго порядка.
Рассмотрим линейное дифференциальное уравнение вида
![]()
где p, q − постоянные коэффициенты. Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение :
![]()
Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:
Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k1 и k2 действительны и различны. В этом случае общее решение описывается функцией
![]()
где C1 и C2 − произвольные действительные числа.
Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k1 второго порядка . Общее решение однородного дифференциального уравнения имеет вид:
![]()
Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k1 = α + βi, k1 = α − βi. Общее решение записывается в виде
![]()
Характеристическое уравнение.
Во многих случаях физические процессы,
происходящие в системах, описываются
системой обыкновенных линейных
дифференциальных уравнений с постоянными
коэффициентами, которая в достаточно
общем случае может быть сведена к
дифференциальному уравнению вида
![]() (при
F(t) (≡) 0 это уравнение называется
однородным). Здесь а1, b1 — постоянные
коэффициенты, выражающиеся, например,
через аэродинамические коэффициенты;
Z(t) — неизвестная функция времени t; F(t)
— заданное, зависящее от времени внешнее
возмущение. Если ввести обозначение
di/dti = pi
так, что
diZ(t)/dti = piZ(t),
то
это уравнение можно переписать в виде
L(p)Z(t) = S(р)F(t),
где L(р) и S(р) — некоторые
многочлены степеней n и m соответственно.
Полученный таким образом многочлен
L(р) = рn + a1pn—1 + ... + an—1p + an
называется
характеристическим многочленом
(полиномом), а уравнение
L(р) = 0
—
характеристическим уравнением (существуют
и другие способы получения X. у. — см.,
например, ст. Передаточная функция).
Корни X. у. определяют вид решения
линейного однородного дифференциального
уравнения и тем самым тип собственного
движения системы (периодические,
затухающее и т. п.). X. у. линейной системы
не зависит от того, относительно какой
из её переменных (например, скорость
полёта или угол атаки при исследовании
продольного движения) составляется
дифференциальное уравнение и какие
возмущающие и задающие воздействия в
эту систему вводятся.
Необходимым
и достаточным условием устойчивости
решения системы обыкновенных линейных
дифференциальных уравнений является
отрицательность всех действительных
частей корней X. у. При этом оказывается,
что положительность всех коэффициентов
характеристического полинома является
необходимым и достаточным условием
устойчивости для систем первого и
второго порядков и лишь необходимым
условием устойчивости (обеспечивается
отрицательность только вещественных
корней) для систем третьего и более
высоких порядков. Существуют различные
способы исследования на основе X. у.
устойчивости систем, например метод
построения областей устойчивости,
алгебраические и частотные критерии.
X. у. широко используется при исследовании
динамики полёта, устойчивости ЛА и его
управляемости.
(при
F(t) (≡) 0 это уравнение называется
однородным). Здесь а1, b1 — постоянные
коэффициенты, выражающиеся, например,
через аэродинамические коэффициенты;
Z(t) — неизвестная функция времени t; F(t)
— заданное, зависящее от времени внешнее
возмущение. Если ввести обозначение
di/dti = pi
так, что
diZ(t)/dti = piZ(t),
то
это уравнение можно переписать в виде
L(p)Z(t) = S(р)F(t),
где L(р) и S(р) — некоторые
многочлены степеней n и m соответственно.
Полученный таким образом многочлен
L(р) = рn + a1pn—1 + ... + an—1p + an
называется
характеристическим многочленом
(полиномом), а уравнение
L(р) = 0
—
характеристическим уравнением (существуют
и другие способы получения X. у. — см.,
например, ст. Передаточная функция).
Корни X. у. определяют вид решения
линейного однородного дифференциального
уравнения и тем самым тип собственного
движения системы (периодические,
затухающее и т. п.). X. у. линейной системы
не зависит от того, относительно какой
из её переменных (например, скорость
полёта или угол атаки при исследовании
продольного движения) составляется
дифференциальное уравнение и какие
возмущающие и задающие воздействия в
эту систему вводятся.
Необходимым
и достаточным условием устойчивости
решения системы обыкновенных линейных
дифференциальных уравнений является
отрицательность всех действительных
частей корней X. у. При этом оказывается,
что положительность всех коэффициентов
характеристического полинома является
необходимым и достаточным условием
устойчивости для систем первого и
второго порядков и лишь необходимым
условием устойчивости (обеспечивается
отрицательность только вещественных
корней) для систем третьего и более
высоких порядков. Существуют различные
способы исследования на основе X. у.
устойчивости систем, например метод
построения областей устойчивости,
алгебраические и частотные критерии.
X. у. широко используется при исследовании
динамики полёта, устойчивости ЛА и его
управляемости.
