Общая теория линий второго порядка.

§1. Общее уравнение линии второго порядка.

Мы рассматривали классификацию линий и определение порядка алгебраических линий в зависимости от вида их уравнений относительно прямоугольной системы координат. Эта классификация и понятие имеет место также и относительно аффинной системы координат. В связи с этим важное значение имеет следующая теорема.

ТЕОРЕМА 1. Если линия, определяемая уравнением

(1)

относительно аффинной системы координат является алгебраической линией n-го порядка, то и относительно любой аффинной системы координат она является алгебраической линией n-го порядка.

Так как данная линия алгебраическая n-го порядка относительно аффинной системы координат , то есть многочлен n-й степени переменных x и y. Найдем уравнение данной линии в аффинной системе , положение которой относительно системы координат определено единичными векторами

,

и началом , при этом

.

Формулы преобразования аффинной системы координат в аффинную систему координат имеют вид:

(2)

Подставив эти выражения и через и в левую часть уравнения (1), получим:

и уравнение данной линии относительно системы координат в виде

.

Так как в формулах (2) и линейно выражаются через и , то очевидно, что есть многочлен переменных , степени . Покажем, что степень m многочлена не может быть меньше степени n многочлена . Допустим, что . Так как

,

то существует преобразование

(3)

обратное преобразованию (2). Если и в функции заменим по формулам (3), то

.

Таким образом, получаем, что линейное преобразование (3) преобразует многочлен в многочлен , степень которого n выше степени m многочлена , что невозможно. Итак, есть многочлен переменных , степени n, а, следовательно, данная линия является алгебраической линией n-го порядка и относительно аффинной системы координат .

Поставим задачу: установить, какие линии определяются общим уравнением второй степени

. (4)

Вместо при различных и будем этот коэффициент обозначать также ; таким образом, . При таком обозначении коэффициентов уравнения второй степени все формулы и уравнения, которые мы получили при изучении линий второго порядка, имеют симметричный вид.

Члены , , таким образом, ициент оюозначать также определяюат ой линией азует многочлен в зависимости от вида их уравнений относительно назовем старшими членами уравнения (4). Коэффициенты могут быть любыми действительными числами, но в старших членах они не должны быть равны нулю одновременно.

Линия второго порядка вполне определена, если задать значения коэффициентов в уравнении (4). Если линия второго порядка задана какими-либо геометрическими условиями, например, достаточным числом точек, расположенных на ней, то для определения уравнения этой линии нужно по данным условиям вычислить коэффициенты уравнения (4). Так как в уравнении (4) хотя бы один из коэффициентов в старших члена отличен от нуля, то, разделив на него обе части уравнения, мы получим уравнение, ему равносильное, в котором будет пять неизвестных коэффициентов. Для их определения зададим пять точек:

,

расположенных на искомой линии.

Уравнение искомой линии можно получить следующим образом. Координаты точек должны удовлетворять уравнению (4), то есть

(5)

Рассмотрим системы (4), (5), состоящие из шести линейных однородных уравнений с шестью неизвестными .

Для того чтобы существовало ненулевое решение этой системы, необходимо и достаточно, чтобы определитель, составленный из коэффициентов при неизвестных , был равен нулю, то есть координаты текущей точки искомой линии удовлетворяли равенству:

.

Если ранг матрицы

(6)

равен 5, то последнее равенство не есть тождество. Оно есть уравнение искомой линии.

ТЕОРЕМА 2. Если из пяти данных точек никакие четыре не лежат на одной прямой, то ранг матрицы (6) равен 5, то есть через пять данных точек проходит единственная линия второго порядка.

Доказательство. Рассмотрим два случая.

Никакие три из пяти данных точек не принадлежат одной прямой.

Чтобы упростить подсчет ранга матрицы (6), отнесем данные точки к новой системе координат, оси которой содержат по две из данных точек, а начало координат не является данной точкой. Такие прямые, очевидно, существуют. Тогда в новой системе координат (рис. 1) данные точки имеют координаты , где ни одно из чисел не равно нулю, и - различные числа. Тогда матрица (6) примет вид:

.

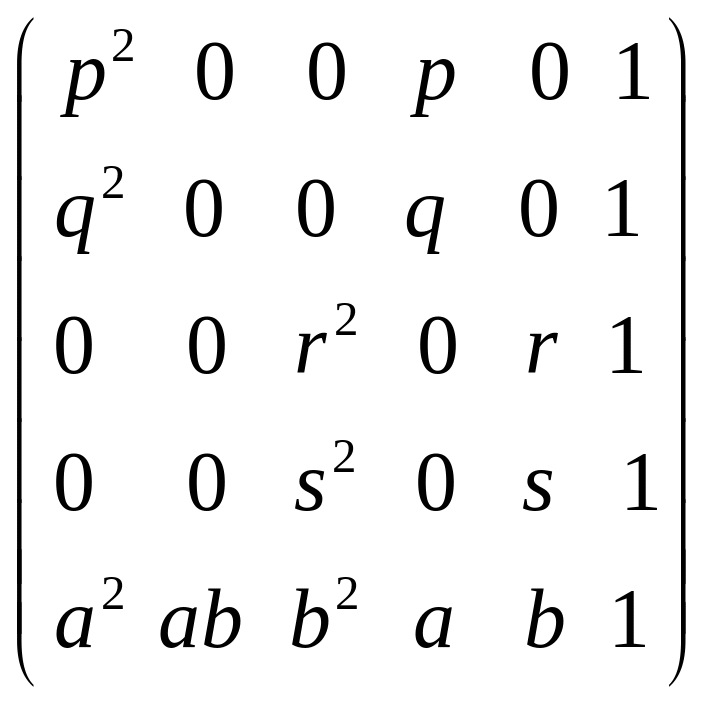Ранг этой матрицы равен 5, так как определитель

.

Следовательно, уравнение искомой линии (4) определено относительно системы . Совершив преобразования системы координат в систему , относительно которой были заданы пять точек , мы получим уравнение линии относительно системы . Указанное преобразование к первоначальной системе координат необходимо производить и в последующих случаях.

Рис. 1 Рис. 2

Рассмотрим второй случай, когда три точки, например, , лежат на одной прямой. Тогда за ось новой системы координат примем прямую, содержащую точки , а за ось - прямую (рис. 2). В системе данные точки имеют координаты: , где

. (*)

Тогда первые три уравнения системы (5) принимают вид:

Определитель этой системы

в силу соотношений (*) и потому . Тогда из последних двух уравнений системы (5) имеем:

. (**)

Если точка не принадлежит прямой (рис 2), то и из соотношений (**) следует, что , .

Таким образом, уравнение искомой линии будет , и, следовательно, линия состоит из двух прямых:

и .

Если же принадлежит прямой (рис 3), то , и из уравнений (**) следует, что . Уравнение линий имеет вид:

,

то есть линия состоит из пары пересекающихся прямых и .

Рис. 3 Рис. 4

ТЕОРЕМА 3. Если четыре точки принадлежат одной прямой a, а точка не принадлежит ей, то существует бесчисленное множество линий второго порядка, проходящих через точки , причем каждая линия состоит из прямой a и произвольной прямой, проходящей через точку .

Доказательство. Примем прямую a за ось , а за ось - прямую, проходящую через точку и точку прямой a, не совпадающую с (рис. 4). Тогда данные точки в системе будут иметь следующие координаты: . Числа - различные и отличные от нуля, и . Система уравнений (5) в рассматриваемом случае примет вид:

(7)

В системе уравнений (7) неизвестные , так как определитель

В этом случае четвертому уравнению системы (7) удовлетворяет любое значение , а из пятого уравнения следует

,

И уравнение искомой линии будет следующее:

Что и доказывает теорему.

ТЕОРЕМА 4. Если пять данных точек принадлежат одной прямой а, то существует бесчисленное множество линий второго порядка, проходящих через них, причем каждая линия состоит из данной прямой а и произвольной прямой плоскости.

Доказательство. Примем за ось прямую а, а за ось - произвольную прямую, проходящую через точку . Доказательство теоремы (3) получаем, если в уравнениях (7) положить . Тогда и уравнение линии будет

что и доказывает теорему.

Из приведенных выше рассуждений следует, что две различные линии второго порядка или имеют не более четырех общих точек, или имеют бесчисленное множество общих точек, расположенных на одной прямой.

Уравнение линии второго порядка, проходящей через пять данных точек , из которых никакие четыре не находятся на одной прямой, можно составить еще и следующим образом. Составим уравнения прямых

Рассмотрим равенство:

(8)

где и - любые действительные числа, не равные нулю одновременно.

Левая часть равенства (8) не равняется нулю тождественно; можно показать, что в противном случае пара прямых , совпадает с парой прямых , .

При любых значениях и уравнение (8) определяет линию второго порядка, проходящую через точки .

Например, если и , то и и, следовательно, Найдем так, чтобы точка принадлежала линии (8). Имеем:

Так как точка не может принадлежать одновременно двум из рассмотренных прямых, то и не могут быть нулями одновременно.

Пример. Даны точки .

Составить уравнение линии второго порядка, проходящей через данные точки.

1. Составим уравнения прямых

или

или

или

или

2. Составим уравнение линии второго порядка, проходящей через точки: .

(9)

3. Потребуем, чтобы эта линия прошла через точку .

.

Подставляя найденное отношение в уравнение (9), получим уравнение искомой линии:

.