1.числовые множества. ограниченные числовые множества. точная верхняя и точная нижняя оценка.

Множества ,элементами которых являются числа ,называются числовыми.

А={1,2,3,5,7} — множество чисел

Числа вида N = {1, 2, 3, ....} называются натуральными. Натуральные числа появились в связи с необходимостью подсчета предметов.

Числа вида: Z = {... -3, -2, -1, 0, 1, 2, 3, ....} называются целыми числами, т.е. целые числа - это натуральные числа, числа, противоположные натуральным, и число 0.

Целые и дробные числа составляют множество рациональных чисел: Q = Z {nm}, где m - целое число, а n - натуральное число.

числа не являющиеся целыми или дробными называются иррациональными.

Множество всех конечных и бесконечных десятичных дробей называется множеством действительных чисел: рациональных и иррациональных.

R –(содержит рациональные и иррациональные числа)-действительные числа

1/3 =0.333…- рациональные числа. Не существует рационального числа,квадрат которого равен числу 2.

Множества-набор определенных объектов. X,Y,A,B-множества , объекты-элементы , x,y,a,b-объекты,элементы. Множество не содержит ни одного объекта.

ограниченное множество — множество, которое в определенном смысле имеет конечный размер.

Множество вещественных чисел   называется ограниченным сверху, если существует число  , такое что все элементы   не превосходят  :

Множество вещественных чисел   называется ограниченным снизу, если существует число  , такое что все элементы   не меньше  : 

Множество  , ограниченное сверху и снизу, называется ограниченным.

Множество  , не являющееся ограниченным, называется неограниченным. Как следует из определения, множество не ограничено тогда и только тогда, когда оно не ограничено сверху или не ограничено снизу.

Примером ограниченного множества является отрезок  ,

неограниченного — множество всех целых чисел  ,

ограниченного сверху, но неограниченного снизу — луч  ,

ограниченного снизу, но неограниченного сверху — луч  .

Точная верхняя граница (верхняя грань) и точная нижняя граница (нижняя грань) — обобщение понятий максимума и минимума множества соответственно.

Точной (наименьшей) верхней гранью (границей), или супре́мумом (лат. supremum — самый высокий) подмножества   упорядоченного множества (или класса)  , называется наименьший элемент  , который равен или больше всех элементов множества  . Другими словами, супремум — это наименьшая из всех верхних граней. Обозначается  .

 — множество верхних граней  , то есть элементов  , равных или больших всех элементов 

Точной (наибольшей) нижней гранью (границей), или и́нфимумом (лат. infimum — самый низкий) подмножества   упорядоченного множества (или класса)  , называется наибольший элемент  , который равен или меньше всех элементов множества  . Другими словами, инфимум — это наибольшая из всех нижних граней. Обозначается  .

Замечание : В случае  , говорят, что   является максимумом  , т.е.  .

В случае  , говорят, что   является минимумом  , т.е.  .

Кванторы: - для любого,всякого,любой всякий ,-найдется ,существует, - соответствие

- равносильность , (следует) : (I )- такое что или имеет место

2.числовые последовательности. Бесконечно малые числовые последоват. Предел числовой последовательности.

Числовые последовательности

Если для каждого нат. числа n определено некоторое правило сопоставляющее ему число xn, то мн-во чисел х1,х2, … ,хn, … наз-ся числовой последовательностью и обозначается {xn}, причем числа образующие данную посл-ть наз-ся ее эл-ми, а эл-т хn общим эл-том посл-ти .

!Порядок следования эл-тов оч. важен, перестановка хотя бы 2-х эл-тов приводит к др. посл-ти.

Основные способы задан. посл-ти:

а) явный, когда предъявляется ф-ла позволяющая по заданному n вычислить любой эл-т n, т.е. xn=f(n), где f- некоторая ф-ция нат. эл-та.

б) неявный, при котором задается некоторое рекуррентное отношение и несколько первых членов посл-ти.

Пример:

а) xn=5n x1=5, x2=10

б) x1=-2 xn=4n-1 –3, n=2,3… х2=-11, х3= - 4

предел числовой последовательности.

Число   называется пределом числовой последовательности  , если последовательность   является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа  , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

3.теоремы о пределах числовых последовательностей. Замечательные пределы.

(график к 1 зам.пределу)

Предел отношения синуса к его аргументу равен еденице ,когда аргумент стремится к нулю..-первый замеч. Предел.

Теоремы о пределах числовых последовательностей.

• Теорема о пределе суммы:

Пусть lim a_n=a lim b_n=b lim a_n+_n=a+b

^{n+ n+ n+}

Докозательство: a_n=a+_n b_n=b+_n Сложим a_n+b_n=a+b+_n+_n=a+b+_n lim a_n+b_n=a+b

ⁿ⁺

2) Теорема о произведение пределов:

Пусть lim a_n=a lim b_n=b lim a_nb_n=ab

^{n+ n+ n+}

Доказательство: a_n=a+_n b_n=b+_n a_nb_n=(a+_n)(b+_n) a_nb_n=ab+a_n+b_n+_nn=ab+_n lim a_nb_n=ab что и

ⁿ⁺

требовалось доказать.

• Теорема о пределе частного

Пусть lim a_n=a lim b_n=b b0 lim a_n/b_n=a/b

^{n+ n+ n+}

Доказательство: a_n=a+_n b_n=b+_n так как b0, то N₁: n>N₁b_n0

_bn

₀ ^(////////_b^/////////) x

a_n/b_n=a_n/b_n-a/b+a/b=a/b+(ba_n-ab_n)/bb_n=a/b+[b(a+_n)-a(b+_n)]/b(b+_n)=a/b+_n/b(1+b_n/b)

lim a_n/b_n=a/b

ⁿ⁺

4.понятие функции.обратной,суперпозиции функции.предел и непрерывность функции в точке ,на интервале ,на отрезке.

В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества вещественных чисел   или множества комплексных чисел  .

Число b называется пределом функции y=f(x) при х → а, если, по мере того как x, приближается к а – будь то справа или слева значение f(x) неограниченно приближается к b.

Основные свойства предела функции в точке  I. Если функция имеет предел при х → а, то только один.  II. Если функция имеет предел при х → а, то она ограничена в некоторой окрестности точки a. 

III. Если существует   и С-постоянная функция (число), то 

IV. Пусть  , тогда:  1)   2)   3)

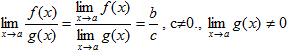
Если условия этих теорем не выполняются, то могут возникнуть неопределенности вида   и др., которые в простейших случаях раскрываются с помощью алгебраических преобразований.

Пример: Вычислить 

Используя свойства предела,

 

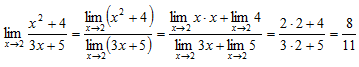
Пусть теперь [a,b]-(замкнутый) отрезок в D(f).Назовём функцию f(x) непрерывной на отрезке [a,b], если f непрерывна на интервале (a,b), непрерывна справа в точке   и непрерывна слева в точке  , то есть           

 Пусть f - некоторая функция, D( f) - её область определения и (a,b) c D ( f) - некоторый (открытый) интервал (может быть, с и/или  )⁷. Назовём функцию f непрерывной на интервале (a,b), если f  непрерывна в любой точке  , то есть для любого   существует   (в сокращённой записи: 

Обратной к данной оборотной функции y=f( x) называется такая функция x= g(y) , которая каждому из множества значений функции y=f(x) ставит в соответствие единое число x из области определения.

На рисунке изображенные функция и обратная к ней функция

5.Производная и дифференциал. Дифференцируемость. Пусть функция у = f(x) определена на некотором интервале (а; Ь).

Проделаем следующие операции:

- аргументу х Е (а; Ь) дадим приращение ∆ x: х +∆x ∈ (а; Ь);

- найдем соответствующее приращение функции: ∆y = f(x+∆x)-

- f(x);

- составим отношение приращения функции к приращению аргу-

мента: ∆у/∆х;

- найдем предел этого отношения при ∆x→0: lim ∆у/∆х .

Если этот предел существует, то его называют производной функ-

ции f(x) и обозначают одним из символов f '(х), у';

Производноit фУН1Сции у = f(x) в mО'Ч1Се хо называется предел

отношения приращения функции к приращению аргумента, когда

приращение аргумента стремится к нулю . записывется это так.

Производная функции f(x) есть некоторая функция г(х), nро'Uзведенная

из данной функции.

~ Функция у = f(x), имеющая производную в каждой точке интервала

(а; Ь), называется дифференцируемоit в этом интервале; операция

нахОЖ,Дения производной функции называется дифференцированием.

Значение производной функции у = f(x) в точке х = хо обозначается

одним из символов : f(хо)

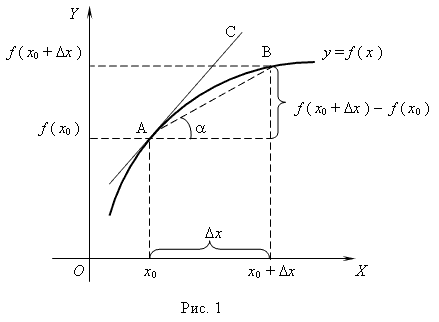
видно, что для любых двух точек A и B графика функции:  

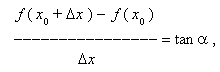где  - угол наклона секущей AB.