Элементы теории графов

Теория графов представляет в распоряжение инженера исклю­чительно удобный аппарат для моделирования структурных свойств систем и отношений между объектами самой разнообразной при­роды. На основе аналогии между физическими величинами развива­ется методика построения математических моделей систем в раз­личной форме.

Основные понятия и определения

Граф — это система некоторых объектов вместе с парами этих объектов, изображаются отношения связи между ними.

Графом G называется система (V,U,), где V={} — множество вершин; U={u} — множество ребер;  — функция инциденции, ста­вящая в соответствие каждому ребру uU упорядоченную (или не­упорядоченную) пару вершин (₁,₂), называемых концами ребра u.

Множество vUu образует множество элементов графа. По количеству элементов графы делятся на конечные и бесконечные.

Если (u)= (₁,₂) — упорядоченная пара, (т.е. (₁ ₂)(₁,₂) (₂,₁)), то ребро  называется ориентированным ребром или дугой, исходящей из вершины ₁ (начало), и входящей в вершину ₂ (конец дуги).

Если (u)=(₁,₂) — неориентированная пара, то соответствую­щее ей ребро — неориентированное.

Граф с неориентированными ребрами называют неориентиро­ванным, а с ориентированными ребрами — неориентированным графом (орграфом).

Всякому графу G(v,u,) можно сопоставить соотнесенный не­ориентированный граф , где— сопоставляет ребрам те же пары вершин, что и, но неупорядоченные.

Граф, имеющий как ориентированные, так и неориентирован­ные ребра, называется смешанным.

Граф G=(v,u,), ребрами которого являются всевозможными пары (u)=(_i,_j) для двух возможных вершин _i,_jV, называется полным неориентированным графом. Такие графы для трех, четырех и пяти вершин приведены:

Граф G=(v,u,), в котором пара вершин соединяется несколькими (кратными) ребрамиб называется мультиграфом, а содержащий изолированные вершины — нуль-графом.

Дополнением графа G=(v,u,) является граф G_к=(v,u,), ребра которого совместно с графом G образуют полный граф.

Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. В общем случае граф может содержать изолированные вершины, которые являются концами ребер и не связаны между собой, ни с другими вершинами.

Число ребер, связанных с вершиной _i (петля учитывается два­жды), называют степенью вершины.

Цепи и циклы графов

Цепь — конечная или бесконечная последовательность ребер S=(…₁,₂,…), в которой у каждого ребра _к одна из вершин явля­ется вершиной ребра _к-1, при этом ребро и одна из вершин могут встречаться несколько раз. Каждая цепь имеет начальную и конеч­ную вершину, остальные вершины называются внутренними (про­межуточными).

Цепь называется простой, если любое реьро не повторяется в цепи дважды. Составной (сложной) в противном случае; элементар­ной, если в ней ни одна из вершин не повторяется дважды.

Цикл — конечная цепь, начинающаяся и заканчивающаяся на той же вершине.

Цикл называется простым, если все его ребра различны, в ином случае — составным (сложным), и элементарным — если при об­ходе его ни одна из вершин не встречается дважды.

Цикл, не содержащий вершины, кроме той, на которой он начи­нается и заканчивается, называется петлей.

Цикл, у которого начальная и конечная вершины различны, на­зывается путем.

Он также может быть простым (никакая дуга не встречается дважды), составным или элементарным (никакая вершина не встре­чается дважды).

Длина пути — число ребер (дуг) в нем.

Цикл, начинающаяся и заканчивающаяся в начальной вершине, называется контуром.

Граф называется конечным, если число вершин его конечно, и бесконечным — в ином случае.

Граф Н(v,u,) называется частичным для графа G(v,u,), если все ребра и вершины графа Н, являются соответственно ребрами и вершинами графа G, т.е. если НG, то для всех  V.

Нуль-граф считается частичным графом любого графа. Все частичные графы Н_i для G(v,u,) можно получить, выбирая в качестве ребер всевозможные подмножества ребер графа G.

Подграфом G_А(А) графа G(v) называется граф, вершинами кото­рого являются вершины Аv, а ребрами — все ребра из G, оба конца которых лежат в А.

Иначе, G_А(А) подграф графа G(v), если Аv и G_А(v)=G(v)А.

Если А=v, то G_А(А)=G(v); если А={а}, т.е. А состоит из одной вершины, то G_А(а) состоит из петель в а; если Аv — подмножество изолированных вершин графа G(v), то подграфом графа G(v) будет нуль-граф.

Частичным подграфом Н_А(А), АХ графа G(v) называется подграф, ребрами которого являются некоторые ребра из G(v), оба конца которых лежат в А.

Иначе, Н_А(А) — частичным подграф графа G(v), если АХ и Н_А(v)=G(v)А для всех vV.

Дополнительным частичным подграфом Н_А(А) графа G(v) является единственный граф, состоящий из ребер графа G(v), не принадлежащих некоторому частичному подграфу Н_А(А) графа G(v).

1 - Граф G(v).

2 - Подграф G_А(А) графа G(v).

3 - Частичный подграф Н_А(А) графа G(v).

4 - Дополнительный частичный подграф Н_А(А) графа G(v).

Звездным графом, определяемым вершиной v, называется граф, состоящий из ребер G(v), имеющих v концевой вершиной. При этом петли в v могут включаться, либо не включаться в звездный граф.

Две вершины _i и _j неорганизованного графа G(v) называются связными, если существуюет цепь S с концами _i и _j. При прохож­дении пути через некоторую вершину _к более одного раза цикл в вершине _к можно удалять из цепи S.

Неориентированный граф называется связным, если любая пара его вершин связана. Отношение связности для вершин графа явля­ется отношением эквивалентности. Оно разбивает множество вер­шин графа на классы.

Подграфы, ''натянутые'' на эти классы вершин, называются компонентами связности графа. Другими словами, компонентами связности неориентированного графа G(v) называется подграф Н_А(А) с множеством вершин Аv и множеством ребер в G(v), инцидентных только вершинам из А, причем ни одна из v_iA не смежна с верши­нами из множества vА.

Несвязный граф состоит из нескольких отдельных частичных подграфов:

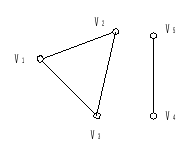
В сильно связанном ориентированном графе для любой пары вершин обязательно существует соединяющий их путь. Компонентой сильной связности ориентированного графа G(v) называется сильно связанный подграф Н_А(А) с множеством вершин Аv и множеством дуг, имеющих начало и конец в множестве А, причем ни одна из вершин v_iA и ни одна из вершин v_j vА не смежны между собой. Очевидно, что сильно связанный ориентированный граф имеет только одну компоненту сильной связности. Пример ориентированного графа, состоящего из 2-х компонент сильной связности, приведен ниже

Отдельными, широко используемыми видами графов являются деревья и прадеревья.

Деревом называется конечный связный граф, состоящий по крайней мере из двух вершин и не содержащий циклов.

Такой граф не имееи кратных ребер:

Ветвями дерева называются ребра графа, входящие в дерево.

Хордами дерева называют ребра, взодящие в граф, дополнительный к данному графу.