28. Сбалансированные деревья. Показатель сбалансированности. Avl-деревья.

Дерево является сбалансированным, если для каждого узла исходящие ветви отличаются по высоте не более, чем на одни уровень.

Показателя сбалансированности:

• Левое (L) - узел левоперевешивающий, если самый длинный путь по ее левому поддереву на единицу больше самого длинного пути по ее правому поддереву

• Сбалансированное (B) - равны наиболее длинные пути по обеим ее поддеревьям

• Правое (R) - узел правоперевешивающий, если самый длинный путь по ее правому поддереву на единицу больше самого длинного пути по ее левому поддереву

Дерево является СБАЛАНСИРОВАННЫМ тогда и только тогда, когда для каждого узла высота его двух поддеревьев различается не более чем на 1.Поэтому деревья, удовлетворяющие этому условию, часто называют "АВЛ-деревьями" (по фамилиям их изобретателей).

AVL-деревья хранят дополнительно в каждой вершине разность между высотами левого и правого поддеревьев, которая в сбалансированном дереве может принимать только три значения: -1, 0, 1. Строго говоря, AVL-деревья не являются сбалансированными в смысле приведенного выше определения. Требуется только, чтобы для любой вершины AVL-дерева разность высот ее левого и правого поддеревьев была по абсолютной величине не больше единицы. При этом длины путей от корня к внешним вершинам могут различаться больше, чем на единицу. Можно, тем не менее, доказать, что и в случае AVL-деревьев их высота оценивается сверху логарифмически в зависимости от числа вершин:

h <= C log2 n

29.Виды балансировки деревьев. Балансировка через массив.

Дерево является сбалансированным, если для каждого узла исходящие ветви отличаются по высоте не более, чем на одни уровень. Операции балансировки: однократный правый(RR), однократный левый(LL), двукратный лево-правый(LR), двукратный право-левый(RL) повороты узлов. Виды балансировки:

1. однократный правый (RR) поворот

2. однократный левый (LL) поворот (выросла левая ветвь)

3. двукратный поворот налево и направо (LR) (выросла правая ветвь)

4. двукратный поворот направо и налево (RL)

5. число вращений не превышает С · h

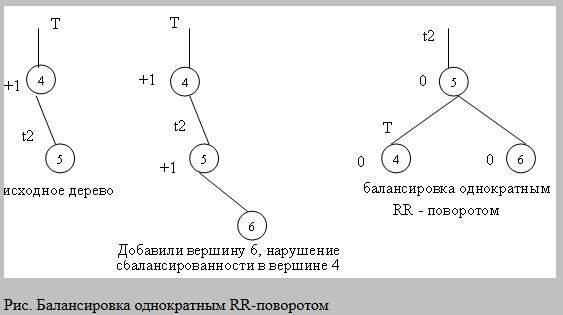
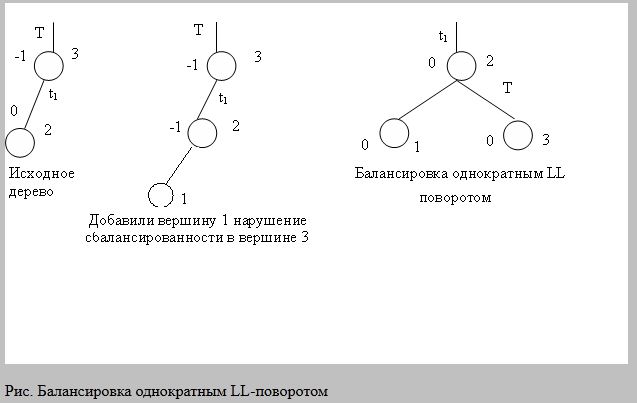Операции с балансированными деревьями: 1) Вставить новый элемент;2)Удалить заданный элемент;3)Поиск заданного элемента. Существуют два принципиально  различные вида балансировки, тогда как остальные виды могут быть получены из этих двух, исходя из соображений симметрии.

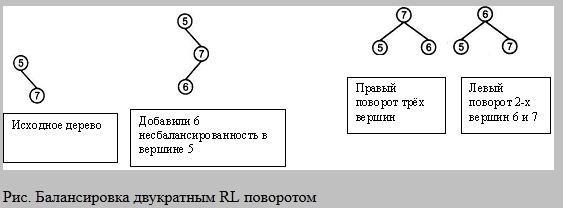
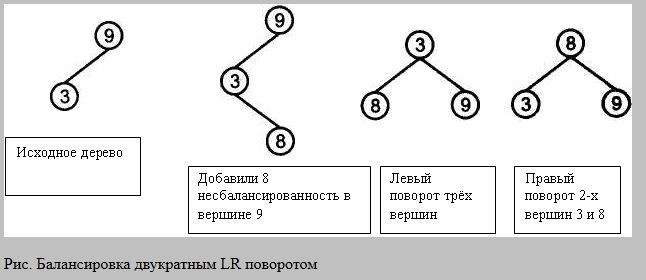
Балансировка через массив:

(1) Скопировать данные из дерева в массив в отсортированном виде (2) очистить дерево. (3)добавить элемент из массива не отсортировано; средний элемент – вершина и т.д.; средний левой части, средний правой части и

т.д.

30. Красно-чёрные деревья.

Исторически AVL-деревья - одна из первых схем реализации почти сбалансированных деревьев. Более популярна другая схема: красно-черные деревья или RB-деревья(Red-BlackTrees). Каждая вершинаRB-дерева окрашена либо в красный, либо в черный цвет. (В реализации за цвет отвечает логическая переменная).Основные свойства:каждая внешняя (или нулевая) вершина считается черной; корневая вершина дерева черная; у красной вершины дети черные;

Всякий путь от корня дерева к произвольной внешней вершине имеет одно и то же количество черных вершин.

Последний пункт определения означает сбалансированность дерева по черным вершинам.

Из пункта 3 определения следует, что в произвольном пути от корня к терминальной вершине не может быть двух красных вершин подряд. Это означает, что, поскольку число черных вершин в любом пути одинаково, длины разных путей к терминальным вершинам отличаются не более чем вдвое. Это свойство близко по своей сути к сбалансированности. Несложно показать, что для красно-черного дерева справедлива следующая оценка сверху на высоту дерева в зависимости от числа вершин:

h <= 2 log2 (n+1)

Из этого следует, что поиск в красно-черном дереве также выполняется за логарифмическое время.

Новая вершина добавляется в красно-черное дерево как терминальная после процедуры поиска (этим RB-дерево ничем не отличается от других упорядоченных деревьев). Новая вершина окрашивается в красный цвет. При этом пункт 3 в определении красно-черного дерева может нарушиться. Поэтому после добавления, а также удаления вершины выполняется процедура восстановления структуры красно-черного дерева, играющая ту же роль, что и восстановление балансировки AVL-дерева. Преимущество красно-черных деревьев состоит в том, что процедура восстановления более простая. Во многих случаях она ограничивается перекрашиванием вершин. В ней также могут выполняться операции вращения вершины влево и вправо, но число вращений может быть не больше двух при добавлении элемента и не больше четырех при удалении.

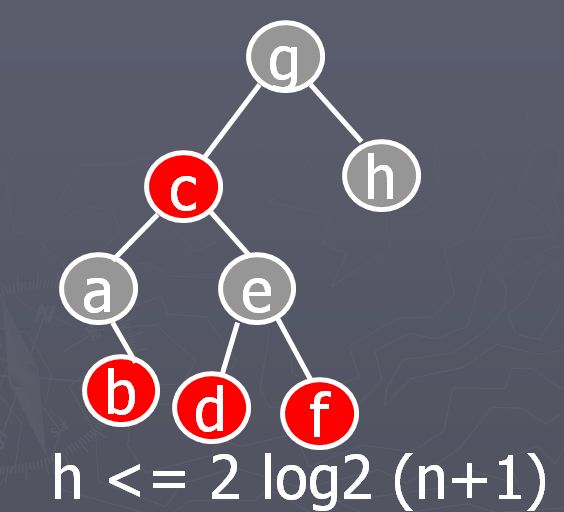
Красно-чёрное дерево (RB-tree) отличается от АВЛ-дерева смыслом признака сбалансированности: вместо разности высот ветвей используется абстрактный "цвет" (красный или чёрный).