Контрольное задание
1.
Составим таблицу
истинности для формулы
,
которая содержит две переменные x
и y.
В первых двух столбцах таблицы запишем
четыре возможных пары значений этих
переменных, в последующих столбцах —
значения промежуточных формул и в
последнем столбце — значение формулы.
Таблица
истинности для формулы
ᵛ
ᵛ
Переменные |
Промежуточные логические формулы |
Формула |
|||||
|
|
|
|
|
|
|
ᵛ ᵛ |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 1, то есть является тождественно истинной.
2. Таблица истинности для формулы :
Переменные |
Промежуточные логические формулы |
Формула |
||||
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
Из таблицы видно, что при всех наборах значений переменных x и y формула принимает значение 0, то есть является тождественно ложной.
Таблица истинности для формулы
:
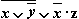Переменные |
Промежуточные логические формулы |
Формула |
||||||
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
Из таблицы видно, что формула в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
Домашнее задание:
Угринович Н.Д. «Информатика и ИКТ» Учебник для 10 класса (Профильный уровень), 4-е издание, М., БИНОМ, Лаборатория знаний, ОАО «Московские учебники», 2008 г., глава 3, § 3.2.1 - 3.2.3.