Рис.3.27
Как было показано, рассмотренные основные кон-структивные признаки только частично определяют каждую конкретную логику. Выработанные в математике приёмы позволяют строить логические теории, описывающие раз-личные явления на множествах объектов самой разной природы.
В науке основополагающая роль логики заключается в формализации знаний, в процессе которой систематизиру-ются соответствующие факты, явления и закономерности, выявляется общность методов исследования в различных дисциплинах, границы применимости теорий и т.д.
Основное практическое значение формализации логи-ческих систем заключается в их последующей реализации при помощи различного рода вычислительных устройств, что позволяет создавать программные продукты и системы (например, робототехнические), обладающие элементами искусственного интеллекта. Применение логических мето-дов при расчете и проектировании сложных технических систем за счёт введения логических связей между объекта-ми позволяет намного упростить оперирование с ними, процессы композиции и декомпозиции.
246
Раздел IV. Теория графов
На начальных этапах анализа и синтеза многие сис-темы зачастую представляют в виде набора некоторых объ-ектов, соединенных между собой связями. Теория графов изучает общие свойства таких структур.
1. Основные понятия теории графов. Примеры её применения
1.1. Псевдографы, графы, способы их задания
Рассмотрим некоторое множество элементов вида Vi (i = 1,…,n) и производное от него множество Х пар элемен-тов из V вида (Vi , Vj), где (1 i, j n).
Определение. Элементы множества V называют вер-шинами. Еcли порядок следования элементов в парах Х = {(Vi , Vj), (1 i, j n)} не зафиксирован, то такие пары назы-вают ребрами, а совокупность G = (V, X) – неориентиро-ванным псевдографом. В том случае, когда все пары Х упорядочены, их называют дугами, а совокупность G = (V, X) – ориентированным псевдографом.
Для краткости прилагательное “неориентированный” в названиях будет опускаться. Графически вершины обычно изображают точками или окружностями малого диаметра, рёбра – линиями, дуги – однонаправленными стрелками.
Определение. Если элементам-рёбрам (элементам-ду-гам) Хij = {(Vi , Vj) } псевдографа G = (V, X) присвоены неко-торые числовые значения dij (1 i, j n), называемые весами рёбер (дуг), то псевдограф называют взвешенным.
Также веса ребер или дуг называют расстояниями. Множество всех весов задается матрицей D размером n n, а весь взвешенный псевдограф обозначается как G=(V,X, D).
247
Пример 1. Псевдограф задан множествами V=(1,2,3); X = ((1,1), (1,1), (1,2), (1,2), (2,3), (3,3), (3,3)). Графическое изображение псевдографа дано на Рис.4.1.
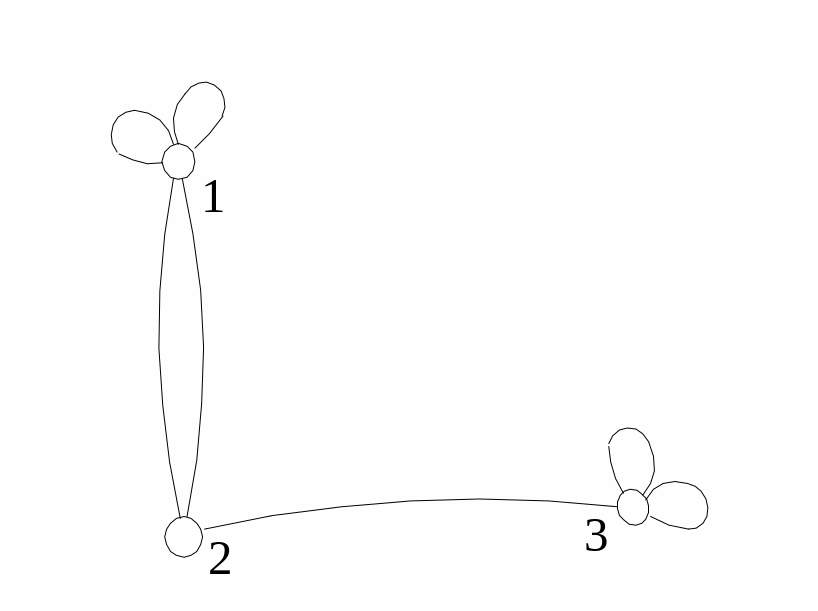
Рис.4.1
Пример 2. Ориентированный псевдограф задан мно-жествами V=(1,2,3); X = ((1,1), (1,1), (1,2), (2,1), (2,3), (3,3), (3,1)). Графическое изображение дано на Рис.4.2.
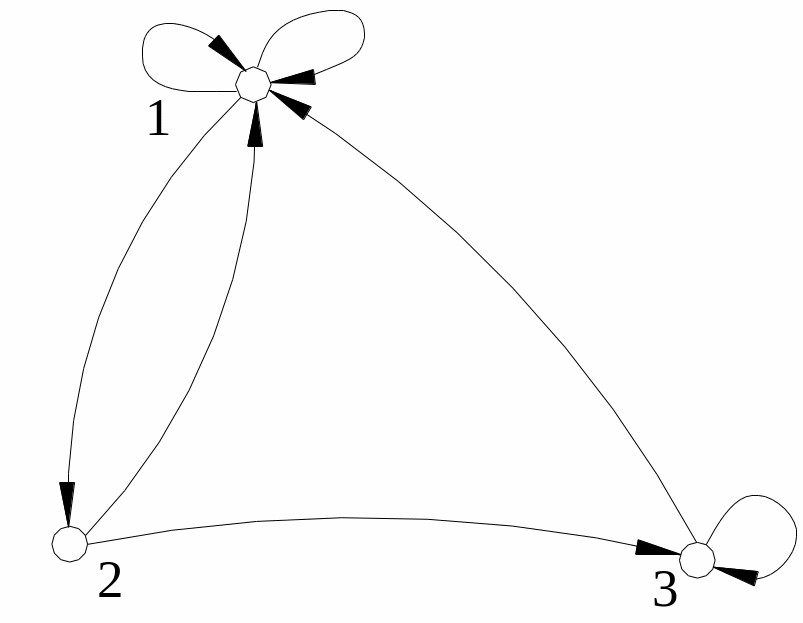
Рис.4.2
Определение. Элементы – рёбра (элементы - дуги) X вида (Vi , Vi ), соединяющие одну и ту же вершину, называют петлями.
Определение. Псевдограф без петель называют муль-тиграфом.
248
Пример 3. Мультиграф, имеющий множества вершин и рёбер V=(1,2,3), Х=((1,2), (1,2), (2,3)), показан на Рис.4.3.
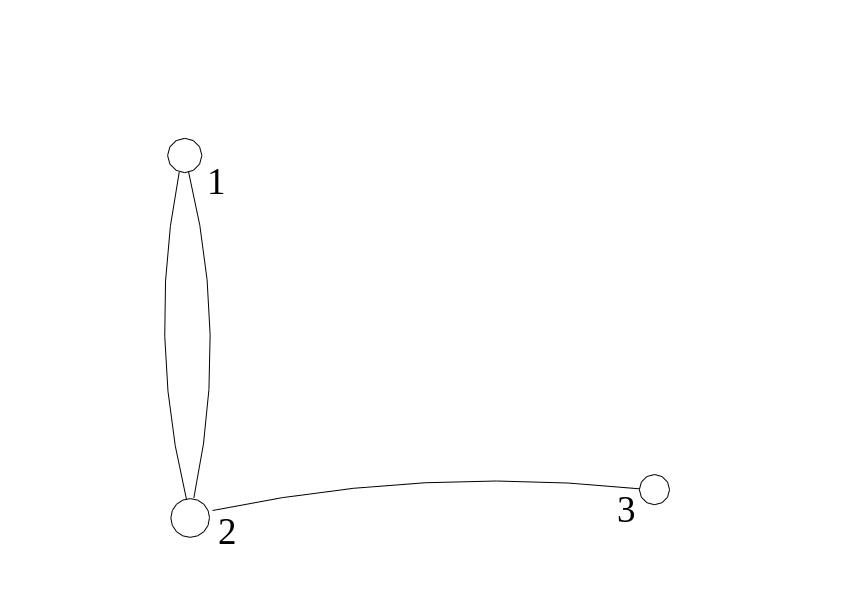
Рис.4.3
Определение. Если в множестве рёбер (дуг) X есть одинаковые элементы, то они называются кратными.
Определение. Мультиграф без кратных ребер назы-вается графом. Ориентированный граф для краткости обозначения называют также орграфом.
Пример 4. V=(1,2,3), X=((1,2),(2,3)). На Рис.4.4 пока-зан граф и орграф с данными множествами (V, X).
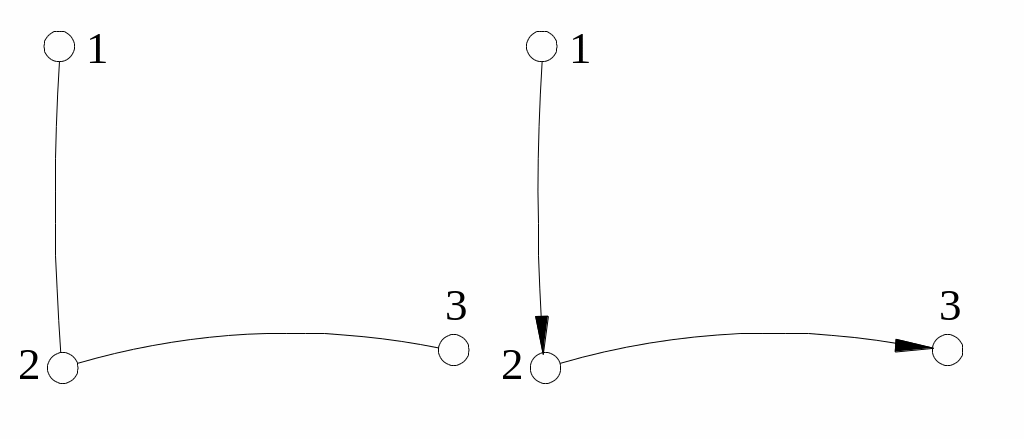
Рис.4.4
Определение. Если вершины графа (орграфа) Vi и Vj соединены ребром (дугой) Хk = (Vi , Vj), то их называют смежными. Вершина Vi и ребро (дуга) Хk = (Vi , Vj), образо-
249
ванные данной вершиной, называют инцидентными.
Определение. Степенью вершины V называются чис-ло d(V) ребер (дуг), инцидентных ей.
Определение. Если d(V)=0, то вершину называют изо-лированной, если d(V)=1, то - висячей.
В Примере 3: d(V1)=2, d(V2)=3, d(V3)=1, вершина V3 – висячая.
Определение. Рассмотрим граф G=(V,X). Граф G1 = (V1 , X1 ) называют подграфом графа G, если V1 V, Х1 Х.
Определение. Последовательность вершин и ребер, связывающих их, называется маршрутом (путем).
В Примере 3 последовательность (V1 Х1 V2 Х3 V3) – маршрут из вершины V1 в вершину V3 .
Определение.Число ребер в маршруте называется длиной маршрута.
Определение. Маршрут, в котором все ребра попарно различны, называется цепью.
Определение. Цепь, в которой все вершины попар-но различны, различны, называется простой цепью.
Определение. Маршрут, в котором начальная и ко-нечная вершины совпадают (V1= Vn), называется циклом.
Определение. Цикл, в котором кроме V1 и Vn все вер-шины различны, называется простым.
Пример 5. V=(1,2,3,4), X=((1,2), (2,3), (3,4), (1,4), (1,3), (2, 4)). Граф показан на Рис.4.5. Номера ребер заданы числами 1-6.
В графе выделены следующие циклы:
(V1 1 V2 2 V3 3 V4 6 V2 1 V1) - цикл длины 5,
(V1 1 V2 2 V3 3 V4 4 V1) - простой цикл длины 4.
Определение. Граф (орграф) называется связным, ес-ли для любых двух его вершин существует цепь, соеди-няющая их.
250
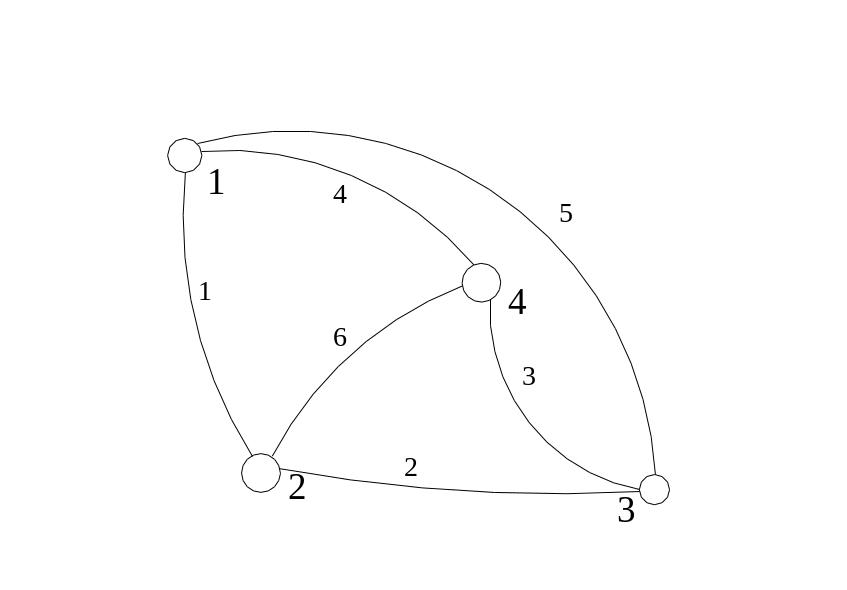
Рис.4.5
Способы задания графов (орграфов).
1. Списки вершин и рёбер (дуг). Множества V и X задают-ся путём перечисления их элементов. Способ рассмотрен в вышеприведенных Примерах.
2. Матрица смежности.
Определение. Матрицей смежности графа G = (V,X ), имеющего n вершин V1,...,Vn , называется квадратная мат-рица А размером n n, у которой каждой строке с номером i (столбцу с номером j) соответствует вершина с номером i (j). Если вершины Vi и Vj смежны, то элемент аi j =1, иначе аi j = 0.
Замечание. У неориентированных графов матрицы смежности симметричны (аij =аji) и их диагональные эле-менты равны нулю: аi i = 0.
3. Матрица инцидентности.
Определение. Матрицей инцидентности графа (ор-графа) G = (V, X) , имеющего n вершин V1 , . . . , Vn и m рё-бер (дуг) Х1 , ... , Хm , называется матрица B размером n m, у которой строкам соответствуют вершины, а столбцам – рёбра (дуги). Если вершина Vi инцидентна с ребром (дугой) Хj , то элемент аi j =1, иначе аi j = 0.
Задачи.
1. Доказать, что в любом связном графе с n вершинами
251
должно быть не менее (n-1) ребра.
2.Построить матрицы смежности и инцидентности для гра-фов, заданных списками:
а) V=(1,2,3), X=((1,2), (1,3)),
б) V=(1,2,3,4), X=((1,2), (1,3), (1,4), (2,3)),
в) V=(1,2,3,4,5), X=((1,3), (1,5), (2,4), (2,5), (3,4),(4,5)),
г) V=(1,2,3,4,5,6), X=((1,3), (1,4), (1,6), (2,4), (2,5),(3,5),(3,6), (4,6)).
3.Построить матрицы смежности и инцидентности для графа из Примера 5.
4
.Построить
матрицы инцидентности для графов,
имеющих следующие матрицы смежности :
Использование графовых представлений систем по-зволяет более наглядно представить их структуру, выявить свойства, пояснить методы исследования. Рассмотрим ос-новные виды графов и примеры их применения в иссле-довании систем разного рода.