- •3Сила Ампера.Взаимодействие проводников с током.Определение единицы силы тока-а.
- •4Сила Лоренца.Движение заряженных частиц в электрическом и магнитном полях.Ускорители заряженных частиц.
- •5Контур с током в однородном и неоднородном магнитном поле.Магнитный момент контура.
- •6Теорема о циркуляции вектора в и ее применение для расчета магнитных полей.
- •7Работа при перемещении проводника и контура с током в магнитном поле.
- •9Явление самоиндукции.Явление взаимоиндукции.Индуктивность(физ.Смысл).
- •10Вращение рамки с током в магнитном поле.Генераторы переменного и постоянного тока.
- •11Магнитное поле в веществе.Вектор намагничивания.Напряженность магнитного поля и ее связь с индукцией.Магнитная проницаемость.Диа-,пара-, и ферромагнетики.
- •12Теория ферромагнетизма.Петля гистерезиса.Коэрцитивная сила (поле), остаточное намагничение.
- •13Свободные колебания.Диф-е ур-ие колебаний,его решение.Формула Томсона.Графики зависимости q,u,I от времени.
- •17Переменный ток.Реактивные сопротивления.Закон Ома для цепи переменного тока.Эффективные значения тока и напряжения.
- •1Свет-электромагнитная волна.Сферическая, плоская волна.Показатель преломления.Полное внутреннее отражение.
- •2Интерференция света.Опыт Юнга.Ширина полос интерференции.
- •3Интерференция в тонких пленках.Просветление оптики.
- •4Полосы равной толщины.Кольца Ньютона в отраженном и проходящем свете.Применение интерференции.
- •5Дифракция света.Принцип Гюйгенса-Френеля.Прохождение света сквозь малые отверстия(метод зон Френеля).
- •6Дифракция на круглом отверстии.Дифракция на круглом диске.
- •7Дифракция Фраунгофера на одной щели.
- •8Дифракционная решетка.Разложение света в спектр с помощью диф-решетки.
- •9Характеристики дифракционных решеток.Критерий Рэлея разрешения двух линий.Дифракция рентгеновских лучей(ф-ла Вульфа-Брэггов).
- •10Дисперсия света.Нормальная и аномальная дисперсия.
- •11Поглощение света.Закон Бугера.
- •12Поляризация света.Закон Брюстера.
13Свободные колебания.Диф-е ур-ие колебаний,его решение.Формула Томсона.Графики зависимости q,u,I от времени.
Если
положение системы в любое время может
быть описано единственным параметром,
то система имеет одну
степень свободы.
Этим параметром может быть, например,
отрезок прямой, отсчитываемый от
некоторой линии или угол, отсчитываемый
от какой-то плоскости. Будем считать,
что в положении устойчивого равновесия
(х=0) потенциальная энергия U=U(x) системы
минимальна U(0)=0. В случае малых колебаний,
разложив функцию U(x) в ряд по степеням
x, ограничимся первыми тремя членами
формулы Маклорена: ![]() ,
т.к. в точке минимума
,
т.к. в точке минимума ![]() ,
а U'' должна быть >0, то
,
а U'' должна быть >0, то ![]() .
Введя обозначение U'(0)=k (k>0)
получаем формулу для потенциальной
энергии
.
Введя обозначение U'(0)=k (k>0)
получаем формулу для потенциальной
энергии ![]() .
Зная вид функции U(x) можно найти величину
силы, действующей на систему
.
Зная вид функции U(x) можно найти величину
силы, действующей на систему ![]() .
Силы вида
.
Силы вида ![]() называются
квазиупругими независимо
от их природы. Эта сила (знак «-») всегда
направлена к положению равновесия и
называются
квазиупругими независимо
от их природы. Эта сила (знак «-») всегда
направлена к положению равновесия и
называется возвращающей силой. Рассмотрим в качестве примера колебательную систему с одной степенью свободы пружинный маятник.
В
смещенном положении ![]() действительно носит характер квазиупругой
силы.
действительно носит характер квазиупругой
силы.
Если
шарик сместить из положения равновесия
на x=a и дать ему свободу, то под действием
квазиупругой силы F шарик будет двигаться
со скоростью ![]() .
Потенциальная энергия при
.
Потенциальная энергия при ![]() будет убывать, а кинетическая энергия
должна возрастать (закон сохранения
энергии). Массой пружины пренебрегаем.
Пройдя положение равновесия
будет убывать, а кинетическая энергия
должна возрастать (закон сохранения
энергии). Массой пружины пренебрегаем.
Пройдя положение равновесия ![]() движение станет замедляться и при x=
- a шарик остановится
движение станет замедляться и при x=
- a шарик остановится ![]() .
При отсутствии трения получим собственные
колебания системы. Основное уравнение
динамики поступательного движения
записывается в данном случае
.
При отсутствии трения получим собственные
колебания системы. Основное уравнение
динамики поступательного движения
записывается в данном случае ![]() ,
обозначив
,
обозначив
![]() имеем
имеем
![]() .
.
Это
дифференциальное уравнение описывает
собственные колебания системы в
отсутствие сил трения. Общее решение
этого дифференциального уравнения
имеет вид: ![]() ,
где
,
где ![]() -амплитуда
колебания,
-амплитуда
колебания, ![]() - циклическая (круговая) частота,
- циклическая (круговая) частота, ![]() - начальная фаза колебания.
- начальная фаза колебания.
Итак, движение системы, находящейся под действием силы вида F=-kx, является гармоническим колебанием.
Найдем уравнение колебаний в контуре без активного сопротивления R. Для удобства сравнения с колебаниями пружинного маятника условимся считать (+) I, заряжающий емкость C.
![]() Закон Ома для участка цепи с
Закон Ома для участка цепи с ![]() :
:
![]()
![]()
![]() ;
; ![]() , поскольку IR=0
(т.к.R=0)
, поскольку IR=0
(т.к.R=0)
![]()
Введя
обозначение ![]() , получим дифференциальное уравнение
свободных колебаний заряда q
в контуре.
, получим дифференциальное уравнение
свободных колебаний заряда q
в контуре.
![]() Из
теории дифференциальных уравнений
известно, решением полученного диф. ур
- я является уравнение вида
Из
теории дифференциальных уравнений
известно, решением полученного диф. ур
- я является уравнение вида
![]() ,
где
,
где ![]() - собственная частота контура. Итак,
поскольку циклическая частота и период
колебаний взаимосвязаны
- собственная частота контура. Итак,
поскольку циклическая частота и период
колебаний взаимосвязаны ![]() ,
можно получить формулу
для периода собственных электрических
колебаний в LC
–контуре, получившей название
формулы
Томсона.
,
можно получить формулу
для периода собственных электрических
колебаний в LC
–контуре, получившей название
формулы
Томсона.
![]() Изменение напряжения на конденсаторе
Изменение напряжения на конденсаторе
![]() также осуществляется по гармоническому
закону
также осуществляется по гармоническому
закону
![]() Изменение
тока в цепи также оказывается гармоническим
колебанием. Действительно,
Изменение
тока в цепи также оказывается гармоническим
колебанием. Действительно,
![]()
Итак,
 .
Индексом
m
в формулах обозначены амплитудные
(т.е., максимальные) значения заряда,
напряжения и тока.
Видим, что при q и
U достигающих максимальных значений
ток становится равным нулю I=0 и наоборот.
Это соотношение было нами уже установлено,
исходя из энергетических соображений.
.
Индексом
m
в формулах обозначены амплитудные
(т.е., максимальные) значения заряда,
напряжения и тока.
Видим, что при q и
U достигающих максимальных значений
ток становится равным нулю I=0 и наоборот.
Это соотношение было нами уже установлено,
исходя из энергетических соображений.
14Затухающие колебания.Диф-е ур-ие,его решение.График q=q(t).Логарифмический декремент затухания.Добротность контура.
В
любой реальной колебательной системе
есть силы, препятствующие свободным
колебаниям. При этом часть энергии
системы безвозвратно теряется и колебания
постепенно затухают. Следовательно,
реальные свободные колебания всегда
являются затухающими.
В общем случае для механических колебаний
сила сопротивления может быть записана
как ![]() ,
где r – коэффициент сопротивления,
а знак «-» обозначает, что
,
где r – коэффициент сопротивления,
а знак «-» обозначает, что ![]() противоположны по направлению. Тогда
основное уравнение динамики для
материальной точки запишется как
противоположны по направлению. Тогда
основное уравнение динамики для
материальной точки запишется как ![]() и, введя обозначение
и, введя обозначение ![]() , получим дифференциальное
уравнение, описывающее затухающие
механические колебания материальной
точки:
, получим дифференциальное
уравнение, описывающее затухающие
механические колебания материальной
точки:
![]()
Его
решение: ![]() .
Периодичность нарушается
.
Периодичность нарушается ![]() ;
;
![]()
![]() .
.
![]() -
коэффициент затухания,
-
коэффициент затухания,
![]() -
собственная (циклическая) частота, А –
амплитуда затухающих колебаний,
уменьшающаяся со временем по
экспоненциальному закону А =
-
собственная (циклическая) частота, А –
амплитуда затухающих колебаний,
уменьшающаяся со временем по
экспоненциальному закону А = ![]()
Затухающие электромагнитные колебания.
В
реальном колебательном контуре часть
энергии идет на выделение джоулева
тепла в проводниках и активном
сопротивлении катушки индуктивности.
Следовательно, свободные колебания в
контуре затухают тем быстрее, чем больше
его активное сопротивление. Если выделить
все активные сопротивления контура в
виде R, то для реального колебательного
контура (при условии I>0 при зарядке
С)![]()
![]()
![]()
![]()
![]()
![]()
![]()
Введем
обозначения: ![]() получаем уравнение для изменения со
временем заряда q
:
получаем уравнение для изменения со
временем заряда q
:
![]() -
коэффициент затухания,
-
собственная (циклическая) частота, q
– заряд на конденсаторе,
-
коэффициент затухания,
-
собственная (циклическая) частота, q
– заряд на конденсаторе,
Это уравнение совпадает по виду с дифференциальным уравнением затухающих механических колебаний.
Его
решение (из теории дифференциальных
уравнений): ![]()
![]()
![]() ,
таким образом, частота затухающих
колебаний (циклическая)
,
таким образом, частота затухающих
колебаний (циклическая) ![]() т.е.
т.е. ![]()
Для U и I получим:
![]()
![]()
Введем
обозначение ![]() ,
,
![]() ,
,
Тогда
 (Вспомним,
что
(Вспомним,
что
![]() )
)
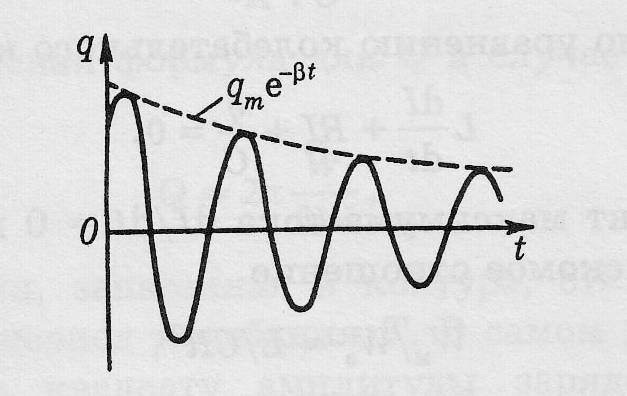
График функции для зависимости q от времени имеет вид
![]()
![]()
![]()
![]() -
сдвиг фаз между током и напряжением
-
сдвиг фаз между током и напряжением
Для характеристики затухания колебаний в контуре вводят понятие логарифмического декремента затухания.
![]()
![]()
Физический
смысл логарифмического декремента
затухания
![]() .
.
Логарифмический декремент затухания – величина, обратная числу колебаний Ne , после совершения которых амплитуда колебаний уменьшается в е раз. Другой важной характеристикой контура является его добротность Q.
![]()
Добротность-
это умноженное на ![]() число колебаний Ne
,
после совершения которых амплитуда
колебаний уменьшается в е раз.
Введем новое обозначение:
число колебаний Ne
,
после совершения которых амплитуда
колебаний уменьшается в е раз.
Введем новое обозначение:
![]()
В
случае слабого затухания колебаний
![]() .
.

15-16Вынужденные колебания
Вынужденные колебания.
Колебания в системе, вызванные внешним периодически изменяющимся воздействием, называются вынужденными.
Рассмотрим колебательный контур, в который последовательно включен источник переменного напряжения.
Uc , UL , UR - напряжения, соответственно, на конденсаторе С, на катушке индуктивности L(на схеме не изображена) и на омическом сопротивлении контура R.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Получили
дифференциальное уравнение вынужденных
колебаний
Решение
этого дифференциального уравнения
представляет собой сумму общего решения
однородного уравнения и частного решения
неоднородного q=q1+q2.
Нас будут интересовать только
установившиеся колебания. Поскольку в
общем решении ![]() стоит множитель
стоит множитель ![]() ,
быстро убывающий со временем, то
вынужденные колебания практически
описываются частным решением
дифференциального уравнения q2,
которое может быть представлено в виде:
,
быстро убывающий со временем, то
вынужденные колебания практически
описываются частным решением
дифференциального уравнения q2,
которое может быть представлено в виде:
![]()
![]()
Или с учетом ранее введенных обозначений
![]()
![]()
Найдем
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
Введем
обозначение ![]() , откуда
, откуда
![]() (*)
(*)
![]()
![]() - в фазе с током
- в фазе с током
![]()
![]() - отстает по фазе от тока на
- отстает по фазе от тока на ![]()
![]()
![]()
![]() - опережает ток по фазе на
- опережает ток по фазе на
Это
может быть представлено с помощью
векторной диаграммы, если изобразить
амплитуды напряжений
URm
=
RIm,
UCm
=
Im
/
![]() ,
ULm
=Im
,
ULm
=Im
![]() и их векторную сумму, равную
и их векторную сумму, равную ![]()
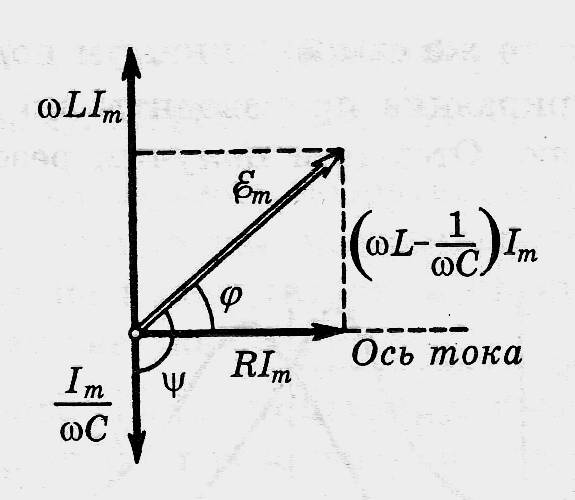
![]() Определенный
из векторной диаграммы тангенс угла
Определенный
из векторной диаграммы тангенс угла
![]() соответствует (*). Векторная диаграмма
здесь изображена для внешнего напряжения,
представленного не как как
соответствует (*). Векторная диаграмма
здесь изображена для внешнего напряжения,
представленного не как как ![]() ,
а как
,
а как
![]() . Величины:
. Величины:
![]() RL
и
RL
и ![]() =
RC
получили
названия индуктивного RL
и емкостного RC
сопротивлений.
=
RC
получили
названия индуктивного RL
и емкостного RC
сопротивлений.