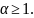- •Тема 2.1. Введение в математический анализ.
- •Тема 2.2. Функции нескольких переменных.
- •Тема 2.3. Интегральное исчисление функции одной переменной.
- •Тема 2.4. Обыкновенные дифференциальные уравнения.
- •Обыкновенные дифференциальные уравнения.
- •Понятие решения.
- •Дифференциальные уравнения первого порядка.
- •Тема 2.5. Числовые и степенные ряды.
Тема 2.3. Интегральное исчисление функции одной переменной.
Первообразная функция и неопределенный интеграл.
Пусть
задана y=f(x)
на некотором множестве Х.
Тогда F(x),
определенная на этом множестве, называется
первообразной для данной функции, если
она дифференцируема для любых х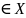 и
F’(x)=f(x)
и
F’(x)=f(x)
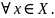 Если F(x)
– первообр-я, то любая ф-ия F(x)+c
, где с-const,
также является первообразной данной
функции: (F(x)+c)’=
=F’(x)+c’=F’(x).
Вся совокупность первообр-х {F(x)+c
| c
} наз-ся НЕОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ ф-ии
y=f(x).
В записи
Если F(x)
– первообр-я, то любая ф-ия F(x)+c
, где с-const,
также является первообразной данной
функции: (F(x)+c)’=
=F’(x)+c’=F’(x).
Вся совокупность первообр-х {F(x)+c
| c
} наз-ся НЕОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ ф-ии
y=f(x).
В записи
 : f(x)
– подынтегр.функция, f(x)dx
– подынтегр.выражение, x
– переменная интегрирования.
: f(x)
– подынтегр.функция, f(x)dx
– подынтегр.выражение, x
– переменная интегрирования.
Основные свойства неопред.интеграла (правила интегрирования):
1) ( )’=f(x)
2)
3)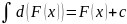
4) (a=const, a
(a=const, a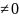 )
)
5)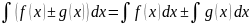
Неопределенные интегралы основных функций.
1)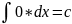
2)
3)
4)
5)
6)
7)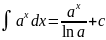
8)
9)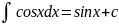
10)
11)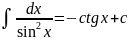
12) |x|<1
|x|<1
13)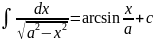 |x|<|a|, a
|x|<|a|, a
14)
 = -arcctgx+c
= -arcctgx+c
15)
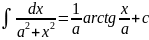 =
=

16)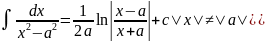
17)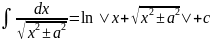
Интегрирование по частям.
Пусть
заданы 2 дифференциальные функции u=u(x)
и v=v(x)
; du(x)=u’(x)dx;
dv(x)=v’(x)dx.
Тогда
 .
.
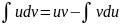 .
Доказательство: Дифференциал от
произведения двух функций равен
d(u*v)=vdu+udv.
След-но, udv=d(uv)-vdu.
Проинтегрируем обе части:
.
Доказательство: Дифференциал от
произведения двух функций равен
d(u*v)=vdu+udv.
След-но, udv=d(uv)-vdu.
Проинтегрируем обе части:

.
.
Замена переменной в неопределенном интеграле (подстановка).
когда нахождение интеграла f(x)dx затруднительно. Подстановки 2-х видов:
Пусть задана х=
 - диффернецируемая по t
функция. В этом сл.
- диффернецируемая по t
функция. В этом сл.

u=
 u-новая
переменная. Формула замены переменной
при такой подставновке:
u-новая
переменная. Формула замены переменной
при такой подставновке:
 .
Это есть подведение ф-ии u=
.
Это есть подведение ф-ии u=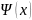 под знак дифференциала и эквивалентна
замене переменной х на новую переменную
u=
.
под знак дифференциала и эквивалентна
замене переменной х на новую переменную
u=
.
Интегрирование рациональных функций.
Функция
называется дробной, если она равна
отношению двух многочленов f(x)= ,
где
,
где
 ;
;
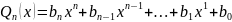 .
Дробь вида f(x)=
называется простой (правильной), если
m<n.
В противном случаем называется
неправильной. Введем понятие простейшей
дроби: ф-ия вида
.
Дробь вида f(x)=
называется простой (правильной), если
m<n.
В противном случаем называется
неправильной. Введем понятие простейшей
дроби: ф-ия вида
 , где r>0
, A,a-числа
и выражение вида
, где r>0
, A,a-числа
и выражение вида
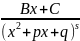 , B,C,p,q
– числа -- это простейшие
выражения. ИНТЕГРИРОВАНИЕ
ПРОСТЕЙШИХ ДРОБЕЙ.
При r≠
, B,C,p,q
– числа -- это простейшие
выражения. ИНТЕГРИРОВАНИЕ
ПРОСТЕЙШИХ ДРОБЕЙ.
При r≠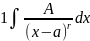 =A
=A . Когда r=1, имеем табличный …=A
. Когда r=1, имеем табличный …=A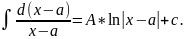 Теперь интегрирование
простейших выражений второго вида:
Теперь интегрирование
простейших выражений второго вида:
 . Рассмотрим
. Рассмотрим
 . Он вычисляется посредством выделения
в числителе производной квадратного
трехчлена.
. Он вычисляется посредством выделения
в числителе производной квадратного
трехчлена.
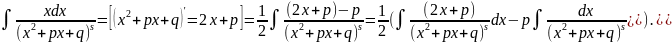 Вычисляем по отдельности. Первый из
полученных – подстановкой:
Вычисляем по отдельности. Первый из
полученных – подстановкой:

 =
= =
= .
Интеграл
.
Интеграл
 при s=1
вычисляется поср-ом выделения полного
квадрата:
при s=1
вычисляется поср-ом выделения полного
квадрата:
 ->
->
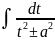 (табличный). При s>1
для вычисления интегралов
(табличный). При s>1
для вычисления интегралов
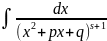 используется
формула следующего вида:
используется
формула следующего вида:
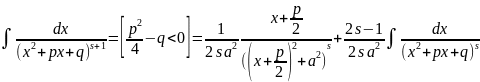 (конспект, м.б.неточно записана!)
(конспект, м.б.неточно записана!)
Интеграл
 интегрируется по тем же формулам с
предварительным выносом коэффициента
при х-квадрат за знак интеграла. =
интегрируется по тем же формулам с
предварительным выносом коэффициента
при х-квадрат за знак интеграла. =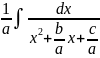 .
.
ИНТЕГРИРОВАНИЕ ПРАВИЛЬНЫХ ДРОБЕЙ Многочлен n-ой степени разлаживается в произведение сл.вида:
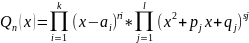 .
Каждому множителю
.
Каждому множителю
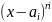 соответствует
сумма простейших дробей
соответствует
сумма простейших дробей
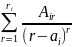 (1). Каждому вида
(1). Каждому вида
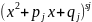 ставится в соответствие сумма
ставится в соответствие сумма
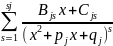 (2).
(2).
 -
коэффициенты, значения неизвестны(непред.
коэф-ты). Используя (1) и (2), отношение
многочленов можно записать в виде сумм:
(где i=1,2…k;
j=1,2…l)
-
коэффициенты, значения неизвестны(непред.
коэф-ты). Используя (1) и (2), отношение
многочленов можно записать в виде сумм:
(где i=1,2…k;
j=1,2…l)
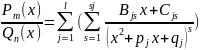 +
+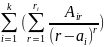 (3) Неизвестные коэффициенты из (3)
находятся с помощью метода
неопределенных коэффициентов: Правая
часть (3) приводится к общему знаменателю.
Далее в числителе получ. выражения
группируются коэф-ты при степенях х
.
(3) Неизвестные коэффициенты из (3)
находятся с помощью метода
неопределенных коэффициентов: Правая
часть (3) приводится к общему знаменателю.
Далее в числителе получ. выражения
группируются коэф-ты при степенях х
.
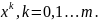 В рез-те правая преобразуется к виду
В рез-те правая преобразуется к виду
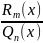 ,
где коэф-ми многочлена
,
где коэф-ми многочлена
 являются неопр. коэффициентами
.
Т.к. выполняется
являются неопр. коэффициентами
.
Т.к. выполняется
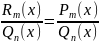 , то коэффициенты многочлена
, то коэффициенты многочлена
 должны быть равны коэф-ам
должны быть равны коэф-ам
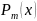 .
.
В результате приравнивания коэф-ов данных многочленов получаем алгебраическую систему уравнений, из которой находятся неопр. коэф-ты .
ИНТЕГРИРОВАНИЕ
НЕПРАВИЛЬНЫХ ДРОБЕЙ. До
интегрирования неправильной дроби
,
где m>n
, проводится деление многочлена
на
 .
Получаем, что
.
Получаем, что

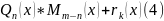 ,
где 0
,
где 0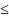 k<n.
Из (4) следует , что отношение
k<n.
Из (4) следует , что отношение
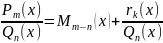 , где
, где
 – правильная дробь. Т.о. получаем: при
m>n
– правильная дробь. Т.о. получаем: при
m>n
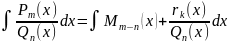
Интегрирование тригонометрических выражений.
Выражений
вида
 .
.
1)
Если m
– нечетное , то
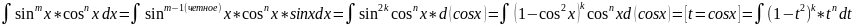
2)
Если n-
нечетное n=2k+1,
под знак подносим cosx:
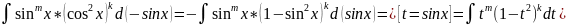 .
В случае, когда n=2k
и m=2l,
используются формулы понижения степени:
sinxcosx=
.
В случае, когда n=2k
и m=2l,
используются формулы понижения степени:
sinxcosx=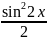 ; 1-
; 1- ;
;
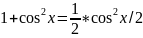
Вычисление
интеграла
 :
вычисляются с применением тригонометрических
ф-ий произведения. Сводятся к вычислению
инт. от суммы.
:
вычисляются с применением тригонометрических
ф-ий произведения. Сводятся к вычислению
инт. от суммы.
Интегрирование
иррац выражений.
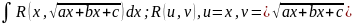 . Данный интеграл с помощью выделения
полного квадрата в квадратном трехчлене
сводится к инт след вида:
. Данный интеграл с помощью выделения
полного квадрата в квадратном трехчлене
сводится к инт след вида:
 (1)
;
(1)
;
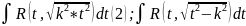 (3) , где
t=x+(b/2a) . Интегралы
вида 1, 2, 3 вычисляются с помощью след
подстановок:
(3) , где
t=x+(b/2a) . Интегралы
вида 1, 2, 3 вычисляются с помощью след
подстановок:
а)
вида (1): подстановки t=k*sin
u
; б) вида (2): подстановки t=k*tg
u
; в)
вида (3): подстановки t=k
/ sin
u.
Применение подстановок а)-в) сводит
интегралы 1-3 к инт-ам:
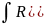 .
.
ВЫЧИСЛЕНИЕ
ИНТЕГРАЛОВ ВИДА
 . Здесь R
(x,y,y1,y2,yk).
Данные интегралы выч-ся с пом подстановки
. Здесь R
(x,y,y1,y2,yk).
Данные интегралы выч-ся с пом подстановки
 , где S
– наим общее кратное чисел n1,
n2,
nk.
, где S
– наим общее кратное чисел n1,
n2,
nk.
Понятие определенного интеграла и его геометрическая иллюстрация. Свойства определенного интеграла.
Пусть
задана y=f(x),
определенная и непрерывная на [a,b].
Разобьем интервал n
точками
 на отрезке [
на отрезке [ ],
где k=1…n
; длины отрезков
],
где k=1…n
; длины отрезков
 . Выберем в каждом из данных отрезков
точку
. Выберем в каждом из данных отрезков
точку
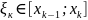 ,
f(
,
f( . Вычислим
. Вычислим
 , k=1…n
Просуммируем данные произведения:
, k=1…n
Просуммируем данные произведения:
 (1) Cумма
(1) наз-ся интегральной суммой ф-ии y=f(x)
на [a,b].
Определение: Если существует конечный
предел инт суммы (1), не зависящей ни от
способа разбиения отрезка [a,b],
ни от выбора точек
(1) Cумма
(1) наз-ся интегральной суммой ф-ии y=f(x)
на [a,b].
Определение: Если существует конечный
предел инт суммы (1), не зависящей ни от
способа разбиения отрезка [a,b],
ни от выбора точек
 , то данный предел наз-ся определенным
интегралом данной ф-ии на отрезке [a,b].
, то данный предел наз-ся определенным
интегралом данной ф-ии на отрезке [a,b].
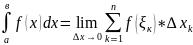 (где дельта х = мах х длин отрезков
разбиения)
(где дельта х = мах х длин отрезков
разбиения)
ГЕОМ СМЫСЛ: Опред интеграл равен алг сумме площадей фигур, ограниченных графиком y=f(x), прямыми x=a, x=b и осью Ох.
СВОЙСТВА:
1)
 ; 2)
; 2)
 =0
; 3)
=0
; 3)
 ; 4)
; 4) ; 5)
; 5)
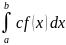 =
=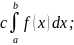 6) Если f(x)
6) Если f(x)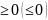 для
для
 и a<b,
то )
и a<b,
то )
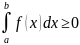 (
( ; 7) Если
; 7) Если
 для
и a<b,
то
для
и a<b,
то
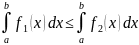 ; 8) Если f(x)
интегрируема на отрезке [a,b]
и
; 8) Если f(x)
интегрируема на отрезке [a,b]
и
 на [a,b],
где m,
M
– некоторые числа, то
на [a,b],
где m,
M
– некоторые числа, то
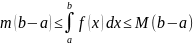 ;
9) Если f(x)
непрерывна на отрезке [a,b]
, то существует такая точка
;
9) Если f(x)
непрерывна на отрезке [a,b]
, то существует такая точка
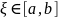 ,
что справедливо равенство
,
что справедливо равенство
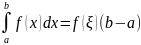 (теорема
о среднем значении); 10)Если ф-ия f(x)
непрерывна и Ф(х)=
(теорема
о среднем значении); 10)Если ф-ия f(x)
непрерывна и Ф(х)=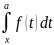 , то справедливо равенство Ф’(x)=f(x),
т.е. производная опред интеграла от
непрерывной ф-ии f(x)
по его переменному верхнему пределу х
существует и равна значения подынт ф-ии
при том же х. Если функция f(x)
непрерывна на отрезке [a,b]
и F(x)
– какая-либо первообразная для f(x)
на этом отрезке, то справедлива ф-ла
Ньютона-Лейбница:
, то справедливо равенство Ф’(x)=f(x),
т.е. производная опред интеграла от
непрерывной ф-ии f(x)
по его переменному верхнему пределу х
существует и равна значения подынт ф-ии
при том же х. Если функция f(x)
непрерывна на отрезке [a,b]
и F(x)
– какая-либо первообразная для f(x)
на этом отрезке, то справедлива ф-ла
Ньютона-Лейбница:

Формула Ньютона- Лейбница. Если функция f(x) непрерывна на отрезке [a,b] и F(x) – какая-либо первообразная для f(x) на этом отрезке, то справедлива ф-ла Ньютона-Лейбница:
Замена
переменной и интегрирование по частям
в определенном интеграле. МЕТОД
ПОДСТАНОВКИ.
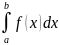 Выберем х=
, которая дифференцируема на [
Выберем х=
, которая дифференцируема на [ . Если х=
. Если х=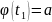 и х=
и х=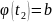 ,
то исх интеграл
,
то исх интеграл
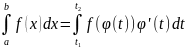 .
Отличие метода подстановки для
определенного интеграла – нет возврата!
.
Отличие метода подстановки для
определенного интеграла – нет возврата!
ПО
ЧАСТЯМ: Пусть заданы u=u(x),
v=v(x)
, диф-емые на [a,b].
Тогда
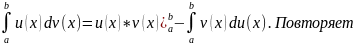 ф-лу инт-ия по частям для неопр интеграла.
ф-лу инт-ия по частям для неопр интеграла.
Геометрические приложения определенного интеграла.
Применяется
для вычисления площадей плоских фигур,
длин плоск кривых и объемов тел в
3D.ПЛОСКИХ
ФИГУР:
Криволинейной трапецией наз-ся плоская
фигура, огр графиком y=f(x) на [a,b],
прямыми x=a
, x=b
и осью Ох. 1)S=
; 2) Плоская фигура ограничена y=f(x),
y=g(x),
определенные на [a,b]
и g(x)
на [a,b],
прямыми x=a
, x=b
и осью Ох. 1)S=
; 2) Плоская фигура ограничена y=f(x),
y=g(x),
определенные на [a,b]
и g(x)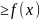 для любых x
для любых x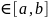 . S
вычисляется по ф-ле: S=
. S
вычисляется по ф-ле: S= ; 3)Вычисления y=f(x),
y=g(x)
, диф-ые на [a,b]
. g(x)
для любых x
В этом случае S=
; 3)Вычисления y=f(x),
y=g(x)
, диф-ые на [a,b]
. g(x)
для любых x
В этом случае S=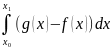 , где х0, х1 – решение ур-ия g(x)=f(x).
, где х0, х1 – решение ур-ия g(x)=f(x).
ОБЪЕМ
ТЕЛА ВРАЩЕНИЯ : Пусть функция y=f(x)
непрерывна на отрезке [a,b
]. В этом случае объем тела, образованного
вращением около оси 0x
криволинейной трапеции, ограниченной
графиком функции y=f(x),
прямыми x=a
, x=b
и осью абсцисс , может быть найден по
формуле:
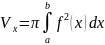 . Если вращение происходит вокруг оси
0у, то объем тела вращения находится по
формуле:
. Если вращение происходит вокруг оси
0у, то объем тела вращения находится по
формуле:

ПЛОЩАДИ
ПОВ-ТЕЙ ТЕЛ ВРАЩЕНИЯ: 1)
y=f(x)
непрерывна на отрезке [a,b
] – в случае вращения графика этой ф-ии:
S=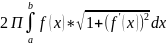 ; 2) В случае параметрического задания
дуг кривой: x=x(t),
y=y(t),
t[t1,t2]
; 2) В случае параметрического задания
дуг кривой: x=x(t),
y=y(t),
t[t1,t2]
S=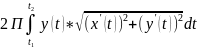 ; 3) В случае задания дуги кривой уравнением
r=r(
; 3) В случае задания дуги кривой уравнением
r=r( в полярных координатах
в полярных координатах

 .
.
ДЛИНА
ДУГИ: Под длиной дуги понимается предел,
к которому стремится длина ломаной
линии, вписанной в эту дугу, при условии,
что количество звеньев ломаной линии
неограниченно возрастает, и при этом
длина наибольшего звена ломаной стремится
к нулю. Если дуга задана непрерывно
дифференцируемой функцией y=f(x) , то ее
длина l вычисляется по формуле :

Понятие о несобственных интегралах и их сходимости.
Интегралы с бесконечными пределами интегрирования и интегралы от неограниченных ф-ций газ несобственными интегралами.
Пусть
ф-я
 непрерывна на промежутке
и интегрируема на любом конечном его
отрезке
непрерывна на промежутке
и интегрируема на любом конечном его
отрезке
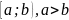 .
Тогда несобственным интегралом с
бесконечным верхним пределом наз предел
.
Тогда несобственным интегралом с
бесконечным верхним пределом наз предел
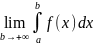 ,
к-й обознач символом
,
к-й обознач символом
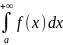 ,
т.е.
,
т.е.
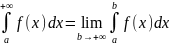 Если
предел сущ и конечен, то несобственный
интеграл наз сходящимся, в противном
случае – расходящимся.
Если
предел сущ и конечен, то несобственный
интеграл наз сходящимся, в противном
случае – расходящимся.
Аналогично
опред несобств интегралы на промежутке
и
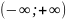 :
:


Если
сходятся оба интеграла в правой части
последней формулы, то интеграл
 наз сходящимся, и расходящимся, если
хотя бы 1 из них расходится. Если f(x)
непрерывна
для всех х
отрезка [a,b],
кроме точки с,
в к-й f(x)имеет
разрыв II рода, то по определению имеет
разрыв II рода, то по определению
наз сходящимся, и расходящимся, если
хотя бы 1 из них расходится. Если f(x)
непрерывна
для всех х
отрезка [a,b],
кроме точки с,
в к-й f(x)имеет
разрыв II рода, то по определению имеет
разрыв II рода, то по определению
 ,
где
,
где
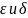 изменяются независимо друг от друга.
изменяются независимо друг от друга.
Несобственный
интеграл
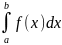
 наз сходящимся, если оба предела в правой
части равенства существуют, и расходящимся,
если не существует хотя бы 1 из них.
наз сходящимся, если оба предела в правой
части равенства существуют, и расходящимся,
если не существует хотя бы 1 из них.
В
случае с=а
или
c=b
получаем
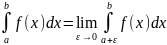
 ,
или
,
или
 . При исследовании сходимости несобств
инт-ов пользуются одним из признаков
сравнения. 1) Если ф-ии f(x)
и
. При исследовании сходимости несобств
инт-ов пользуются одним из признаков
сравнения. 1) Если ф-ии f(x)
и
 определены на промежутке [a;
+
определены на промежутке [a;
+ ),
интегрируемы на отрезке [a,A],
где A
),
интегрируемы на отрезке [a,A],
где A и 0
и 0 для всех x
,
то из сходимости интеграла
для всех x
,
то из сходимости интеграла
 следует сх-ть интеграла
следует сх-ть интеграла
 ,
а из расходимости интеграла
вытекает расх-ть инт-ла
.
(признак сравнения). 2) Пусть на
промежутке [a;
+
)
определены 2 положительные функции f(x)
и
,
инт-емые на любом конечном промежутке
[a,b].
Тогда , если существует конечный предел
,
а из расходимости интеграла
вытекает расх-ть инт-ла
.
(признак сравнения). 2) Пусть на
промежутке [a;
+
)
определены 2 положительные функции f(x)
и
,
инт-емые на любом конечном промежутке
[a,b].
Тогда , если существует конечный предел
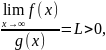 то
интегралы
и
сходятся и расх-ся одновременно
(предельный признак сравнения).
3)Если интеграл
то
интегралы
и
сходятся и расх-ся одновременно
(предельный признак сравнения).
3)Если интеграл
 сходится, то сходится и инт-л
.
В этом случае инт-л
называется абсолютно сходящимся. 4)
Если при x
-> +
ф-я f(x)>0
является бесконечно малой порядка
по сравнению с
сходится, то сходится и инт-л
.
В этом случае инт-л
называется абсолютно сходящимся. 4)
Если при x
-> +
ф-я f(x)>0
является бесконечно малой порядка
по сравнению с
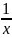 ,
то интеграл
сходится при
,
то интеграл
сходится при
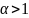 и расходится при
и расходится при
 На практике часто для сравнения
используется ф-ия
На практике часто для сравнения
используется ф-ия
 .
Известно, что
.
Известно, что
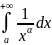 сходится при
и расх-ся при
Аналогичные признаки сх-ти можно указать
и для инт-ов от разрывных ф-ий. Для
сравнения в признаке 4) используют инт-л
сходится при
и расх-ся при
Аналогичные признаки сх-ти можно указать
и для инт-ов от разрывных ф-ий. Для
сравнения в признаке 4) используют инт-л
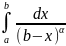 (
( или
или
 ,
который сходится при
,
который сходится при
 и расх-ся при
и расх-ся при