4.Баллистические характеристики трт

Оптимальные баллистические параметры двигателя и ракеты могут быть

реализованы лишь при оптимальных баллистических характеристиках топлива и

прежде всего скорости горения. Для количественной оценки скорости горения ТРТ

используют скорость перемещения точек поверхности горения по нормали и

определяют ее по зависимости

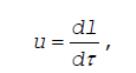
где dl - толщина сгоревшего слоя топлива за время dτ.

В общем случае скорость горения зависит от состава, структуры топлива и

условий горения: давления в камере сгорания, температуры заряда, скорости

движения продуктов сгорания вдоль поверхности горения, ускорения,

действующего нормально к поверхности горения, уровня напряженно-

деформированного состояния заряда и других факторов.

Скорость горения топлива можно рассматривать как проектный параметр

ракеты. В общем случае основные параметры ракеты - максимальная дальность,

скорость в конце АУТ и продолжительность АУТ, зависят от удельного импульса,

относительной массы топлива, а также начальной тяговооруженности ракеты,

характеризующей ее ускорение:

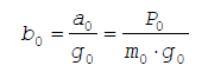
Эффективность применения ТРТ зависит не только от уровня скорости

горения, но и от параметров, характеризующих ее чувствительность к внешним

воздействующим факторам, прежде всего к давлению в камере сгорания и

температуре заряда. Из тепловой теории горения ТРТ следует, что с повышением

температуры заряда скорость горения возрастает. На практике влияние

температуры при р = const оценивают эмпирическими зависимостями вида

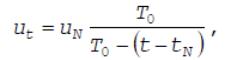
где u_t - скорость горения при температуре t;

u_N - скорость горения при нормальной температуре;

T₀ - эмпирическая константа, зависящая от характеристик топлива и

давления, называемая термохимической константой топлива.

Рассчитывают T0 по формуле

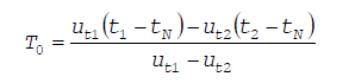
где к_t - температурный градиент скорости горения, 1/град вычисляемый по

формуле

Температурный градиент, выраженный в процентах, называют температурным

коэффициентом скорости горения:

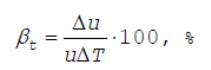
Для оценки температурной чувствительности скорости горения баллиститных порохов и БТРТ принято использовать преимущественно термохимическую константу Т₀. Уровень Т₀ промышленных составов находится в пределах 250…650°C. Для смесевых ТРТ используют, как правило, к_t или β_t, величина которого составляет β_t = 0,1…0,3 %/град. Можно показать, что между Т₀ и к_t существует простая зависимость:

Зависимость скорости горения топлива от давления в камере сгорания

называют законом горения. В широком диапазоне давлений она имеет немонотонный характер и, как правило, с увеличением ρ_К возрастает. Обработка результатов экспериментальных данных дает различные виды аппроксимирующих зависимостей u(p) в разных интервалах давлений. Универсальным обобщением этой зависимости принято считать выражение вида u=a +bp^ν, где а, b и ν - параметры, зависящие в общем случае от состава, структуры топлива и условий горения. Чаще всего a≥0, b>0; ν = 0…1. В отдельных случаях величина v может быть отрицательной и больше 1. В диапазоне давлений до 30 МПа, характерных для РДТТ, функция u(р) аппроксимируется степенной зависимостью u=bp^ν. В случае более высоких давлений, характерных для стволов артиллерийских орудий,

предпочтительна линейная зависимость u=a+bp .

На практике чувствительность скорости горения к изменению давления

независимо от вида аппроксимирующей функции оценивают относительной величиной

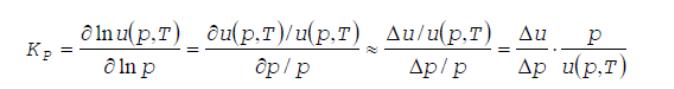
В случае степенной аппроксимации

для соответствующего диапазона PК. Для линейной зависимости

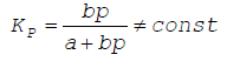и зависит отдавления. На установившемся режиме давление в камере сгорания выражается формулой Бори

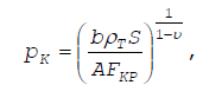
где А - коэффициент истечения.

Следовательно, отклонения давления связаны с отклонениями характеристик

заряда и двигателя зависимостью

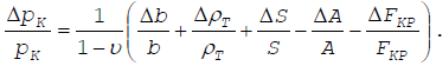
Аналогично вариации других внутрибаллистических характеристик РДТТ (тяги,

расхода) также пропорциональны коэффициенту 1/(1-ν), называемому

коэффициентом усиления. Чем больше величина ν, тем больше изменяется давление (расход, тяга) при случайном изменении плотности, площади поверхности горения и других параметров при прочих равных условиях. Так, если ν=0,1 , то 1/(1-ν)≈1,1, а при ν=0,9 - 1/(1-ν)≈10

Следовательно, при изменении одного из параметров топлива или двигателя

на 1% изменение давления в камере двигателя (тяги, расхода) будет в 9 раз

больше, если топлива с ν=0,1 заменить на топлива с ν=0,9. Разбросы давления

приводят либо к увеличению пассивной массы двигателя, либо к уменьшению

номинального давления. Разбросы расхода сказываются главным образом на

разбросах тяги и, следовательно, влияют на точность поражения цели и выбор

программы тангажа. Расчеты показывают, что при уменьшении ν на 0,1 (v<1)

дальность полета трехступенчатой ракеты может увеличиться до 70 км, что

равноценно уменьшению пассивной массы на 7 кг.

Из уравнения Бори следует, что лишь при ν<l возможна устойчивость

рабочего процесса нерегулируемых РДТТ. Это наглядно можно показать графически (рис. 5). Случайные изменения Δр при ν<1 не вызывают изменения рабочего режима - давление возвращается к равновесному значению. При ν>1 повышение давления вызывает дальнейший рост р_К, а возмущение (-Δp_K) - падение р_K, т.е. режим неустойчивый.

Величина параметра ν влияет такие на чувствительность давления в камере к

изменению температуры заряда. При b=f(T) :

При :

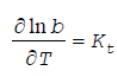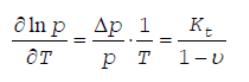
Отсюда .

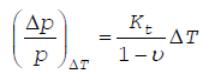Следовательно, изменение равновесного давления при изменении начальной

температуры заряда определяется не только температурным градиентом давления,

но и показателем ν в законе скорости горения. Для получения стабильных

характеристик РДТТ, уменьшения их разброса в широком температурном диапазоне необходима низкая чувствительность скорости горения топлива к давлению и температуре.

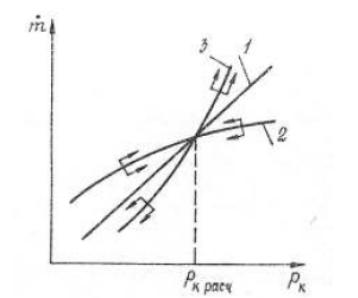
Рис.5. Зависимость газоприхода и газорасхода от давления:

1 - расход через сопло; 2 - приход при ν<1; 3 - приход при ν>1

Для двигателей с управляемой величиной тяги от величины ν зависит

оперативность управления. Используя выражения для вариации давления и тяги,

можно показать, что в случае нерегулируемого сопла и

при регулируемом сопле. Следовательно, с увеличением ν оперативность

регулирования растет. На рис.6. показаны расчетные зависимости изменения

тяги двигателя при изменении давления в результате изменения FКР. В случае

использования топлива с ν = 1,5 при десятикратном изменении давления

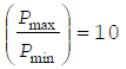глубина регулирования тяги увеличивается в 12 раз по сравнению с

топливом, имеющим ν = 0,5.

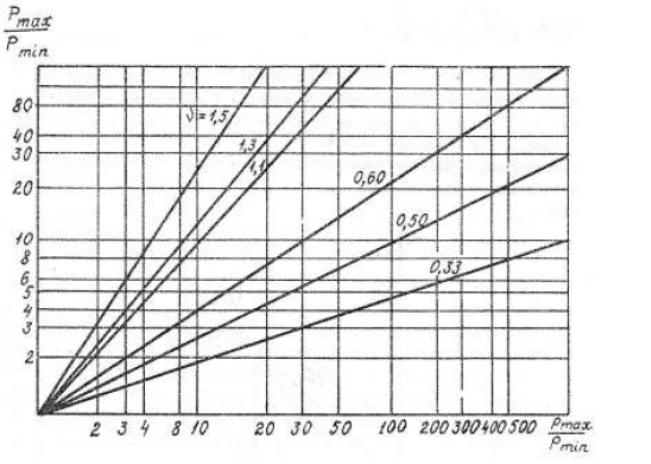
Рис.6. Зависимость диапазона тяги двигателя от изменения давления (FKP)

и величины ν

Список литературы:

1. Абугов Д.И., Бобылев В.М. Теория и расчет ракетных двигателей твердого

топлива. - М.: Машиностроение, 1987.

2. Алемасов В.Е., Дрегалин А.Ф., Тишин А.П. Теория ракетных двигателей. -

М.: Машиностроение, 1989.

3. Волков Е.Б., Мазинг Г.Ю. Сокольский В.Н. Твердотопливные ракеты.

История. Теория. Конструкция. - М.: Машиностроение, 1992.

4. Григорьев А.И. Твердые ракетные топлива. - М.: Химия, 1969.

5. Ерохин Б.Т. Теория внутрикамерных процессов и проектирование РДТТ. -

М.: Машиностроение, 1991.

6. Колотилов А.В., Бугримов А. Л. Прочность и механическая надежность

зарядов твердого топлива и средств пироавтоматики. - М.: МО РФ, 1997.

7. Мальцев В.М., Мальцев М.И., Кашпоров Л.Я. Основные характеристики

горения. - М.: Химия, 1977.

8. Ракетные топлива / Под ред. Я.М.Паушкина, А.3.Чулкова. - М.: Мир,

1975.

9. Фахрутдинов И.X., Котельников А.В. Конструкция и проектирование

ракетных двигателей твердого топлива. -М.: Машиностроение, 1987.

- 18 -