22. Применение принципа максимума
Принцип максимума удобен для использования. В частности, с его помощью вычислялись траектории первых спутников.
При применении в основном используют 2 подхода:
1 Улучшение допустимых управлений.
Пусть дано некоторое
управление
.
Вычисляем для него траекторию
,
и сопряжённую
Вычислим гамильтониан:
и
Затем:
.
Если
,
то, очевидно, управление
удовлетворяет условию максимума, то
есть является экстремальным (подозрительным
на оптимальное управление) согласно
принципу максимума.
Если
и максимум достигается на некотором
,
то по этому
-малом
строят игольчатую вариацию.
Из доказательства
теоремы 2 видно, что существует такое
ε,
что
то есть можно построить лучшее управление.
С ним описанную операцию улучшения
можно повторить.
2 Краевая задача принципа максимума.
Пусть в задаче
функция f
такая, что
можно при каждом фиксированном
вычислить
,
и пусть
аргумент этой максимизации.
Тогда построим краевую задачу:
Система (17) – это
система из 2n
дифференциальных уравнений относительно
неизвестных x(t)
и
и тогда управление
,
очевидно, удовлетворяет условию максимума
и является экстремальным (то есть
подозрительным на решение).
19.Пример в тоу(теория оптимального управления).
Пусть n=2,
r=1
– уравнение движения,начальные
условия:
,
время
.Мн-во
– терминальный
критерий качества.
Выберем в качестве управления u(t):
.
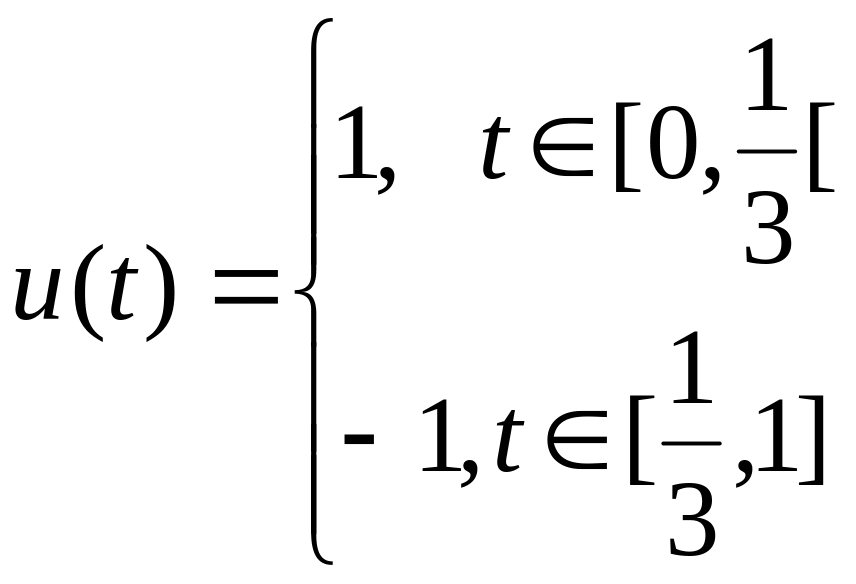Очевидно, оно
допустимое управление, так как одна
точка разрыва
Подсчитаем
порожденную этим управлением
траекторию.Рассмотрим
,
тогда из 1-го уравнения получим:
.
аналогично находим:
Рассмотрим
:
2 Посчитаем цену этого управления:
3 Проверим для
нашего управления выполнение условия
максимума. Для этого нужно подсчитать
сопр.траекторию
:
Составим сопр.
сист.:
Решим эту систему:
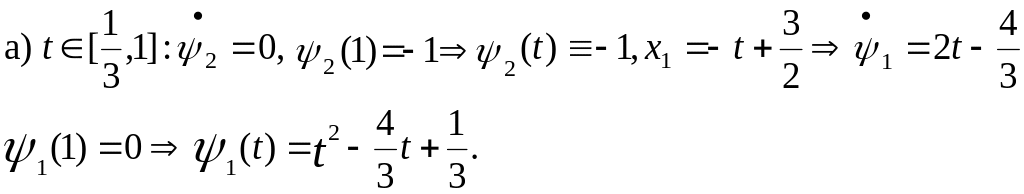
б) Подсчитаем на
4 Условие максимума.
Имеем:
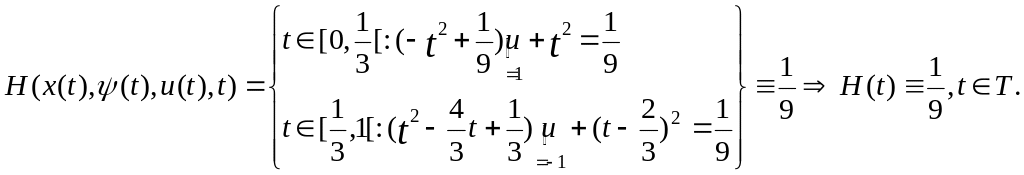Подсчитаем
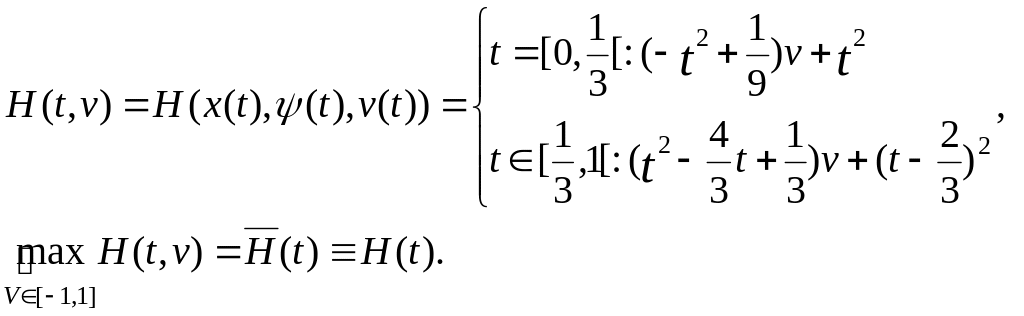
Наше исх. управление уд. усл. max и явл. экстремальным .
5 Покажем, что это
управление не является опт-м. Это
означает, что принцип максимума не
является достаточным условием
оптимальности.Выберем другое управление
и подсчитаем траекторию:
и тогда
Таким образом,
То есть управление
лучше чем
не является оптимальной.
20. Решение терминальной задачи, методом динамического программирования
1 этап. Инвариантное погружение.
Рассмотрим
произвольное число
,
и будем рассматривать траектории на
.
Получим задачу:
(18)
где
– это часть допустимых управлений.
Это и будет семейство
терминальных задач зависящие от двух
параметров:
.
Если в этом семействе
положим
,
то придём к исходной задаче.
Оптимальное
значение функционала в (18) назовём
функцией
Беллмана
и будем обозначать
.
2 этап. Построение уравнения Беллмана.
Возьмём
некоторое положительное число
и положим:
u(t)=v(t)
на
,
где v(t)
– кусок допустимого управления.
Под воздействием
v(t)
траектория движения перейдёт от вектора
.
Тогда имеем:
(19)
Предположим, что,
начиная с момента
из состояния
,
система управляется оптимальным образом,
тогда по определению функции Беллмана
значение функционала будет следующим:
(20)
Предположим, что
– кусок оптимального управления. Тогда
будет выполняться соотношение:
(21)
(согласно принципу
оптимальности Беллмана, а
здесь кусок оптимальной траектории).
Разложим левые части в (20) и (21) в ряд при малых :
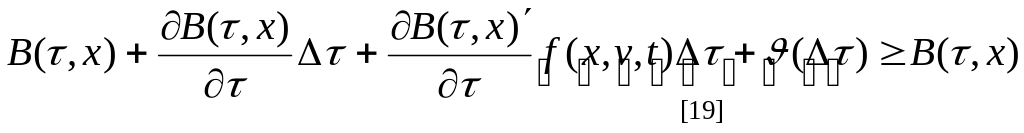(22)
(23)
Сокращая обе части
(22) и (23)
разделив на
и устремив
к нулю получаем:
(24)
Из (24) вытекает:
(25)
(25) – уравнение для функции Беллмана относительно искомой функции . Это есть дифференциальное уравнение в частной производной, осложнённое операцией минимизации.
Чтобы его решить
нужно задать краевые условия: они
получатся из задачи (18), если в ней
положить
(тогда
)
и
то есть
(26)
3 этап. Достаточное условие оптимальности.
Предположим, что мы решили (25) и (26), и построили функцию Беллмана и нашли:
