16. Формула приращения критерия качества.

Относительно задачи (1), (2), (3), будем предполагать, что функции являются непрерывными, .

Согласно этим предположениям задача Коши (1)-(2) имеет и, причём единственное решение.

Возьмём некоторое допустимое уравнение (зафиксированное), и рассмотрим произвольное другое управление . И посчитаем, как изменится функционал при переходе .

Тогда управлению u(t) будет соответствовать траектории х(t), а будет соответствовать другая траектория

Рассмотрим: , функции будут называться приращением траектории и управления.

Введём обозначения: . Эта функция называется сопряжённой функцией.

– эта функция называется гамильтоном, а называется приращение гамильтона при переходе .

С учётом этих обозначений для формулы приращения получаем компактную формулу:

(12)

-малое более высокого порядка чем

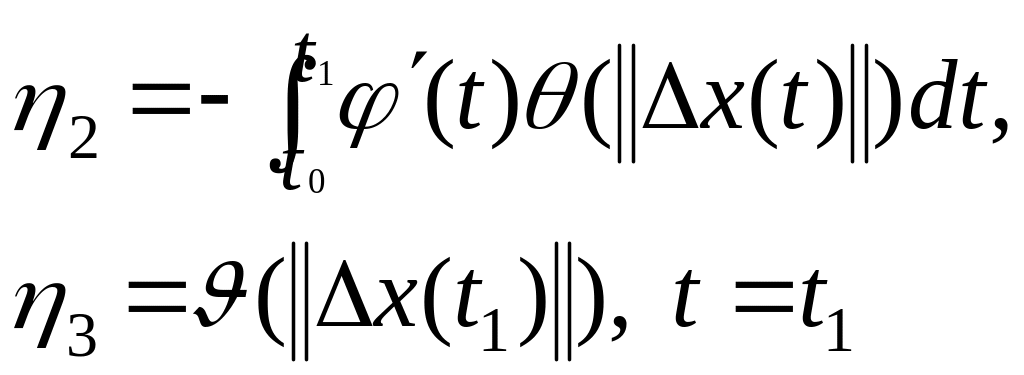
(12) и есть искомая формула приращения.

17. Игольчатая вариация. Оценка приращения траектории

Пусть дано некоторое допустимое управление . Возьмём некоторую внутреннюю точку , некоторый вектор:

Приращение управления будем выбирать следующим образом:

Построенное приращение управления называется игольчатой вариацией , и, видно, что она изменяет исходное управление лишь на отрезке длинной то есть .

При малых ε она похожа на иголку, отсюда и название.

возьмём некоторое , а потом рассмотрим , и для неё

Т. В результате игольчатой вариации справедлива оценка:

(14)

где К некоторая постоянная.

Доказательство.

1. Пусть 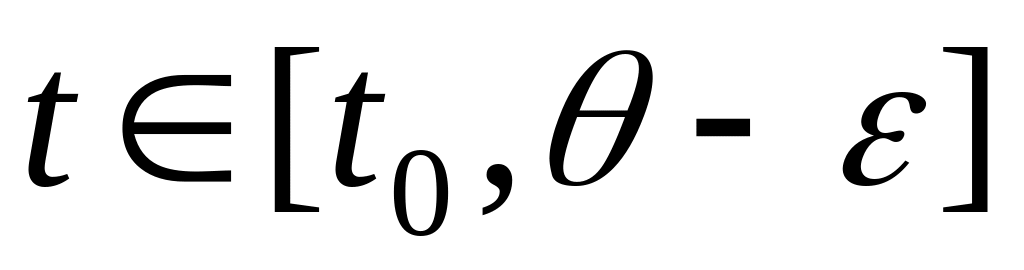. На этом отрезке

2. Пусть 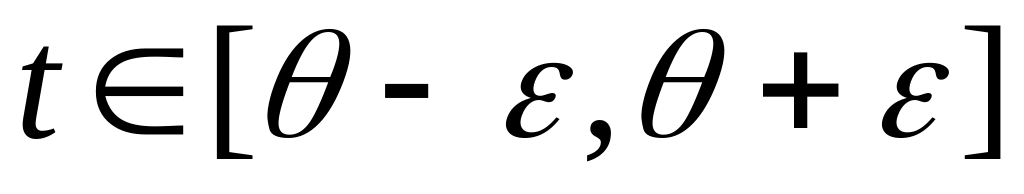так как функция f непрерывна по своим аргументам, управление компактно, тогда и траектория компактна:

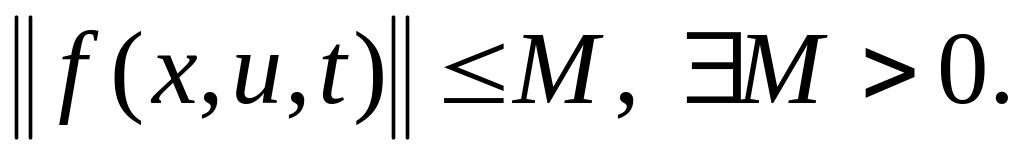
с начальным условием и оценка К=4М

3 , здесь мы получим дифференциальное уравнение:

Чтд

18. Принцип максимума (Понкрягина)

О. Управление будем называть оптимальным управлением, порождённую им траекторию x(t) будем называть оптимальной траекторией, а вычисленную вдоль них функцию будем называть сопряжённой оптимальной траекторией, если выполняется неравенство:

О. Говорят, что допустимое управление (не обязательно оптимальное) удовлетворяет условию максимума, если вдоль него и его траектории гамильтониан достигает своего наибольшего значения на то есть выполняется:

(15)

Т (Принцип максимума). Каждое оптимальное управление должно удовлетворять условию максимума.

Доказательство. Пусть – оптимальное управление, – оптимальные основная и сопряжённая траектории.

Предположим противное. Что это управление условию максимума не удовлетворяет, то есть:

Перенося всё в левую часть получаем приращение:

Построим игольчатую вариацию , при малом ε с указанными , тогда из формулы приращения получаем:

при достаточно малом ε, отсюда

Это противоречит тому, что допустимое управление (ясно, что в результате игольчатой вариации всегда получаем допустимое управление).

Принцип максимума является самым сильным из необходимых условий оптимальности I-го порядка. Можно доказать, что из него вытекает все остальные условия оптимальности, включая условие Эйлера. Однако в общем случае принцип максимума не даёт достаточного условия оптимальности (за исключением линейных систем), то есть не всякое управление, удовлетворяющее условию максимума, является оптимальным.