4.Необходимое условие оптимальности в терминах вариации

Т. Пусть – слабая минималь основной задачи вариационного исчисления, тогда:

1) ;

2) .

Доказательство. 1) Пусть – слабая минималь, предполагаем противное: , тогда из разложения получаем: где предполагаем, что -малое и противоположного знака знаку числа . При достаточно малом . Тогда это неравенство противоречит, что – слабая минималь.

2) Пусть – слабая минималь, предполагаем противное, что существует такая, что . Из разложения имеем:

для достаточно малого , то есть – противоречит, что – слабая минималь.

Ч.т.д.

В частности, условие стационарности из теоремы 1 можно записать в явном виде: если – слабая минималь, то

(4)

5.Условие Эйлера

(1) ,

Лемма (Лагранжа). Если для некоторой непрерывной функции и любой итерации справедливо равенство:

(5)

то отсюда следует, что .

Доказательство. От противного: пусть выполняется (5), но тем не менее существует . Так как функция входит в (5) линейно, то , а в силу непрерывности можно считать, что – внутренняя точка на , более того существует малое .

Выберем в (5) в качестве , так как изображено на рисунке.

Подставим в левую часть (5) и подсчитаем:

. Противоречие с условием (5).

Ч.т.д.

Теорема 2(условие Эйлера). Если – слабая миниамаль основной задачи вариационного исчисления, то она необходимо всюду на [a,b] должна удовлетворять уравнению

(уравнение Эйлера) (6)

(то есть при подстановке в уравнение (6) должна обращать его в верное тождество на [a,b]).

Доказательство. Пусть – слабая миниамаль, тогда для неё вып.-ся (4). Второе слагаемое в (4) проинтегрируем по частям:

.

.

.

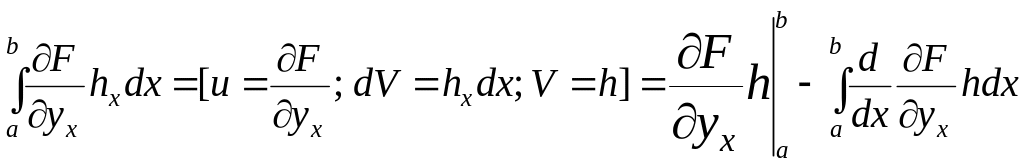Ч.т.д.

6. Обсуждение условий Эйлера

решение ОЗВИ надо искать только среди решений уравнения (6).

Распишем подробно уравнение (6):

(6^*)

Предположим, что мы нашли его общее решение на [a, b]:

Выделим из него допустимые кривые. Они выделяются с помощью условий:

– эти функции, допустимые прямые, которые являются решением уравнения Эйлера называется экстремалями ОЗВИ.

Условие Эйлера можно переформулировать: любая слабая минималь находится среди экстремалей задачи.

Для решения ОЗВИ надо: по функционалу построить уравнение Эйлера, решить его, построить экстремали и проверить условия существования решения и условия II-го порядка.

О. Если для функционала , для некоторой допустимой кривой и вариации допустимо представление:

, то функция а(х) на [a,b] называется вариационной производной функционала I вдоль допустимой кривой y и обозначается: или grad(I(y)).

7. Теорема Гильберта

О. Допустимая кривая будет называться неособой, если выполняется условия:

ТКаждая неособая экстремаль дважды непрерывно дифференцируема Доказательство. Пусть –неособая экстремаль, .

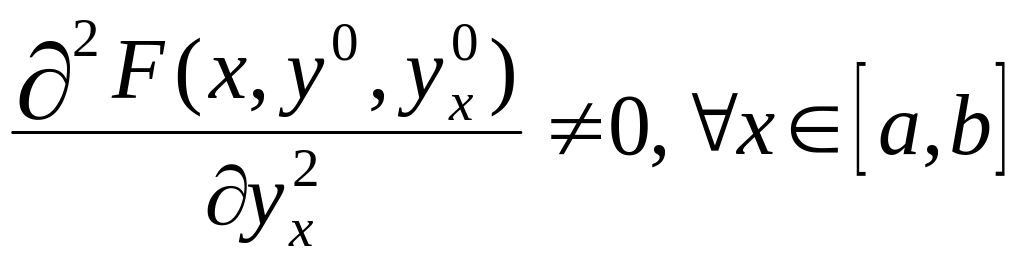Рассмотрим уравнение: где .

т.е. . Поскольку 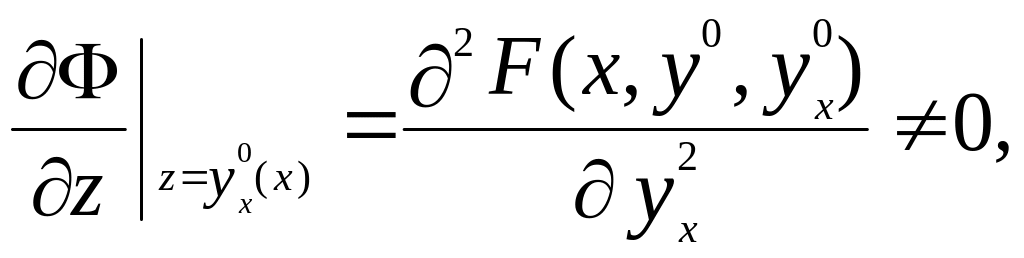то функция удовлетворяет всем условиям теоремы о не явных функциях, а согласно этой теореме так как , то такой же будет и явное решение, то есть , а это означает, что существует , что и требовалось доказать.

Ч.т.д.